«Дилемма заключенных»

«Дилемма заключенных» – это самый известный парадокс во всей теории игр. Такое название этой дилемме дал канадский математик Альберт Такер (1905–1995). Эта игра профессора Такера очень похожа на голливудскую криминальную драму, в которой каждому из двух заключенных предлагают сделку о сотрудничестве с правосудием в обмен на донос о другом заключенном. Эта дилемма наглядно показывает, как трудно может быть действовать сообща для общего блага, если люди преследуют свои личные интересы.

Стимулы, которые мы наблюдаем в «Дилемме заключенных», достаточно часто встречаются и используются учеными при анализе задач в самых разнообразных областях науки, например конкуренция компаний в экономике, общественные нормы в социологии, механизмы принятия решения в психологии, борьба животных за скудные ресурсы в биологии или борьба компьютеров за канал передачи данных.

Алан и Бен угнали машину, но их вскоре поймали. Полицейские подозревают, что до того, как их арестовали, они сбили человека и скрылись с места преступления, но у следствия нет улик, прямо указывающих на их вину. Допрос преступников ведется в разных комнатах.

И у Алана, и у Бена есть два варианта действий: они могут сохранять молчание, а могут признаться. Соответственно, существует четыре возможных исхода этой игры:

Алан сохраняет молчание, и Бен сохраняет молчание;

Алан признается, и Бен сохраняет молчание;

Алан сохраняет молчание, и Бен признается;

Алан признается, и Бен признается.

«Дилемма заключенных» может быть представлена в стратегической форме, при которой каждый ряд матрицы представлял бы возможный выбор Алана, а каждая колонка – возможный выбор Бена. На пересечениях каждого ряда и колонки мы обозначим выигрыши каждого игрока: в данном случае это будет срок заключения.

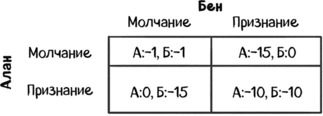
Если Алан и Бен сохранят молчание, то оба получат срок в один год за угон автомобиля. Это отрицательный расклад, поэтому их выигрыши также в минусе (Алан: –1, Бен: –1). Если оба преступника сознаются, каждый сядет в тюрьму на 10 лет (А – 10, Б – 10).

Заключенные понимают, как работает эта матрица, и знают, что имеют дело с одной и той же матрицей.

Это пример игры с одновременными ходами. Даже если заключенные не принимают решения синхронно, мы все равно можем назвать их одновременными, потому что игроки находятся в разных комнатах и ни один из них в момент принятия своего решения не знает, как будет действовать другой.

Однако заметьте, что, воспринимая эту дилемму как игру в стратегической форме, мы не говорим о возможном исходе. Мы просто обозначаем все потенциально возможные итоги, будь они разумны или нет, и записываем выигрыши, которые игроки получили бы, если бы место имел именно такой исход.

Теперь, когда мы записали нашу задачу в стратегической форме, мы можем приступить к анализу возможного результата.

Очевидно, если бы Алан и Бен вместе придумали бы свою версию произошедшего, они смогли бы сохранить молчание и попали бы в тюрьму всего на один год.

Но этот вариант не входит в систему равновесия. Для Алана стратегия «сознаться» строго доминирует над стратегией «молчать»: всегда лучше сознаться, несмотря на его ожидания относительно действий Бена.

Точно так же и для Бена оптимальной стратегией было бы признание, вне зависимости от его ожиданий относительно действий Алана.

В ситуации равновесия Нэша в данной дилемме оба заключенных признаются. Стандартный способ записи этого исхода таков:

{признание, признание}

Это значит, что игрок, чьи выигрыши записаны в матрице в строку (Алан), сделал выбор в пользу признания, как и игрок, чьи выигрыши записаны в колонку (Бен). В равновесии оба заключенных получают по 10 лет тюремного срока.