Необычайная арифметика

Задача № 15

К арифметическим действиям мы привыкли настолько, что выполняем их автоматически, почти не думая о том, что мы делаем. Но те же действия потребуют от нас немалого напряжения, если мы пожелаем применить их к числам, написанным не по десятичной системе. Попробуйте, например, выполнить сложение следующих двух чисел, написанных по пятиричной системе:

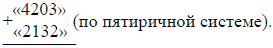
Решение

Складываем по разрядам, начиная с единиц, т. е. справа: 3 + 2 равно пяти; но мы не можем записать 5, потому что такой цифры в пятиричной системе не существует: пять есть уже единица высшего разряда. Значит, в сумме вовсе нет единиц; пишем 0, а пять, т. е. 1-цу следующего разряда, удерживаем в уме. Далее, 0 + 3 = 3, да еще 1-ца, удержанная в уме, - всего 4 единицы второго разряда. В третьем разряде получаем 2 + 1 = 3. В четвертом 4 + 2 равно шести, т. е. 5 + 1; пишем 1, а 5, т. е. 1-цу высшего разряда, относим далее влево. Искомая сумма - 11340.

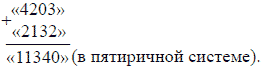
Предоставляем читателю проверить это сложение, предварительно переведя изображенные в кавычках числа в 10-ичную систему и выполнив то же действие.

Точно так же выполняются и другие действия. Для упражнения приводим далее ряд примеров, число которых читатель, при желании, может увеличить самостоятельно:

Задача № 16 Задача № 17 Задача № 18

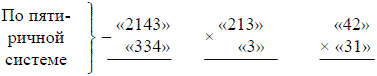
Задача № 19 Задача № 20 Задачи № 21 и № 22

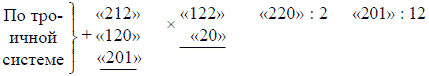
Ответы:

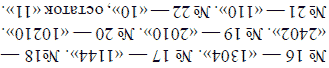
При выполнении этих действий мы сначала мысленно изображаем написанные числа в привычной нам десятичной системе, а получив результат, снова изображаем его в требуемой недесятичной системе. Но можно поступать и иначе: составить «таблицу сложения» и «таблицу умножения» в тех же системах, в которых даны нам числа, и пользоваться ими непосредственно. Например, таблица сложения в пятиричной системе такова:

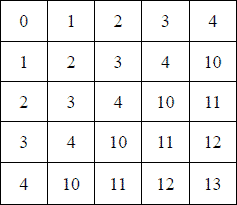
С помощью этой таблички мы могли бы сложить числа «4203» и «2132», написанные в пятиричной системе, гораздо менее напрягая внимание, чем при способе, примененном раньше.

Упрощается, как легко понять, также выполнение вычитания.

Задача № 23

Составим и таблицу умножения («Пифагорову») для пятиричной системы.

Решение

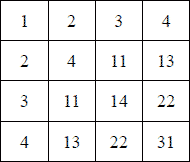
Имея эту табличку перед глазами, вы опять-таки можете облегчить себе труд умножения (и деления) чисел в пятиричной системе, - как легко убедиться, применив ее к приведенным выше примерам. Например, при умножении

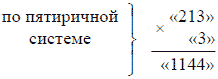
рассуждаем так: трижды три «14» (из таблицы); 4 пишем, 1 - в уме. Один на 3 дает 3, да еще один, - пишем 4. Дважды три = «11»; 1 - пишем, 1 - переносим влево. Получаем в результате «1144».

Чем меньше основание системы, тем меньше и соответствующие таблицы сложения и умножения. Например, для троичной системы обе таблицы таковы:

Таблица сложения для 3-ной системы.

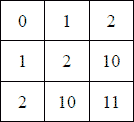
Пифагорова таблица для 3-ной системы:

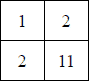
Их можно было бы сразу же запомнить и пользоваться ими для выполнения действий. Самые маленькие таблицы сложения и вычитания получаются для двоичной системы:

Таблица сложения для двоичной системы:

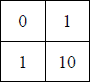
Таблица умножения для двоичной системы:

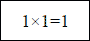
При помощи таких-то простых «таблиц» можно выполнять в двоичной системе все четыре действия! Ум - ножения в этой системе, в сущности, как бы и вовсе нет: ведь умножить на единицу значит оставить число без изменения: умножение же на «10», 100», «1000» (т. е. на 2, на 4, на 8) сводится к простому приписыванию справа соответствующего числа нулей. Что же касается сложения, то для выполнения его нужно помнить только одно - что в двоичной системе 1 + 1 = 10. Не правда ли, мы с полным основанием назвали раньше двоичную систему самой простой из всех возможных? Длинота чисел этой своеобразной арифметики искупается простотой выполнения над ними всех арифметических действий. Пусть требуется, например, умножить:

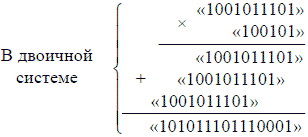
Выполнение действия сводится только к переписыванию данных чисел в надлежащем расположении: это требует несравненно меньших умственных усилий, чем умножение тех же чисел в десятичной системе (605 x 37 = 22385). Если бы у нас была принята двоичная система, изучение письменного счисления требовало бы наименьшего напряжения мысли (зато - наибольшего количества бумаги и чернил). Однако в устном счете двоичная арифметика по удобству выполнения действий значительно уступает нашей десятичной.