Уильям С. Дэвидсон Восходящая шкала размерностей

Приступая к выяснению возможности существования размерности, выходящей за рамки наших современных представлений, нам необходимо воспользоваться аналогией. Сравнивая пространства одного, двух и трех измерений, мы сможем подметить то общее, что позволит нам вывести формулы и, глядя на них, высказать абстрактные суждения о свойствах того или иного тела в четырехмерном пространстве. Дабы не впасть в противоречие, нам необходимо быть столь же осторожными в своих умозаключениях, как астроному, пытающемуся высказывать какие-то утверждения относительно обитателей далекой планеты. Рассматривая условия, делающие возможной жизнь на его собственной Земле, он может подметить ряд закономерностей и попытаться привести их в полную гармонию с условиями, господствующими на интересующем его небесном теле.

Хотя реальные изображения прямых и точек имеют ощутимый размеры по всем направлениям, не следует забывать, что всюду далее мы будем иметь в виду абстрактные прямые и точки. Последние характеризуются лишь положением в пространстве, а первые мы определяем как линии кратчайшего расстояния между двумя точками. Говоря о поверхности, мы также будем иметь в виду лишь абстрактную, воображаемую поверхность независимо от того, располагается ли она свободно в пространстве или ограничивает какое-нибудь тело. Такая поверхность полностью лишена толщины, и бесконечное множество абстрактных поверхностей, наложенных друг на друга, имело бы нулевую суммарную толщину.

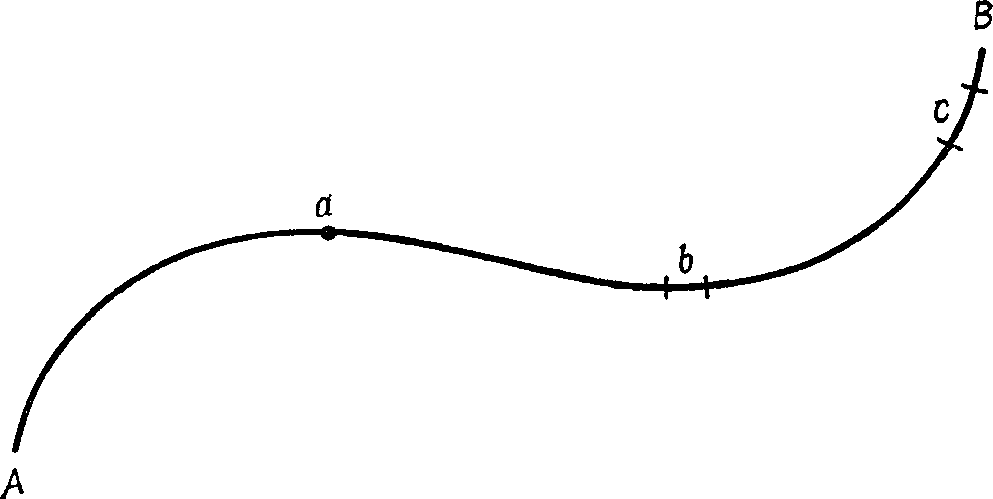
Рис. 1.

Мы начнем с того, что рассмотрим, как ограничено восприятие пространства у существа, живущего в мире одного измерения, то есть на бесконечной кривой в пространстве, конечный отрезок AB которой мы условно изобразим на рис. 1. Предположим, что в различных точках этой кривой находятся три существа a, b и с, причем существо а имеет вид точки, существо b — небольшого отрезка, а существо с по форме напоминает существо b, но имеет несколько большую длину. Мы различаем существа а, b и с по форме потому, что наблюдаем за ними извне. Однако существу а другое существо b представляется в виде точки, так же как существу b — существо с. Такое «точечное» восприятие обусловлено тем, что одномерным существам известно лишь расстояние (вдоль кривой) и положение на ней. Все остальное, что так или иначе связано с каким-нибудь третьим геометрическим свойством, для одномерных обитателей кривой лишено смысла. Существо а, наблюдая существо b, может видеть его лишь в виде точки, потому что смотрит «в торец» отрезку b. Предположим, что существа а, b и с сохраняют свое относительное расположение на кривой на протяжении всей своей жизни. Поскольку каждое из существ в этом случае будет располагать лишь весьма ограниченными сведениями о жизни двух других обитателей кривой, то они будут строить различные умозаключения о том, что представляют собой их соседи. Так, существо а, сознавая собственную точечную форму и видя существо b лишь с «торца», сделает вполне логичный, хотя и неправильный вывод: на кривой обитают лишь точечные существа. Существо b, сознавая свою длину и видя своих соседей а и с в виде точек, решит, что оно удостоилось особой милости творца, вознесшего его в нарушение всех законов природы над его собратьями по пространству.

На рис. 1 мы изобразили произвольную кривую, или траекторию, в пространстве, но для того, чтобы избежать излишних усложнений на последующих рисунках, мы в дальнейшем условимся изображать одномерное пространство в виде прямой. Отрезок прямой можно рассматривать как траекторию точки, ограниченную ее начальным и конечным положением в пространстве. Отрезок прямой — это частный случай движения точки из одного положения в другое по кратчайшему пути AB (рис. 2). Если отрезок AB мы передвинем по кратчайшему пути из начального в конечное положение A'В', то получим плоскую фигуру — прямоугольник. Если отрезок AB переместится по кратчайшему пути па расстояние, равное своей длине (рис. 3), то получится плоская фигура, которая называется «квадрат». Таким образом, квадрат можно назвать элементарной фигурой в двумерном мире, так же как отрезок прямой мы называем элементарной фигурой в одномерном мире.

Переходя от линейного мира к плоскому, мы обнаруживаем, что число различных форм геометрических фигур неизмеримо возросло. Так, в нашем двумерном мире могут существовать не только обитатели, имеющие вид точек и прямолинейных отрезков, но и многочисленные раньше. Точка P будет свободно перемещаться по всей плоскости, явно «не желая» расставаться е двумерным миром, хотя в действительности она принадлежит прямой, способной разместиться лишь в трехмерном пространстве.

Перейдем теперь к рассмотрению знакомых всем нам предметов, а именно предметов, находящихся в трехмерном пространстве. Все формы материи, доступные нашим ощущениям, занимают некоторую часть пространства и обладают длиной, шириной и высотой. Плоскость, прямая и точка существуют в теории лишь для того; чтобы человек мог строить приближенные образы в соответствии с тем, что он наблюдает в материальном мире. Природа действует посредством универсальных законов и строит применительно к условиям, руководствуясь неписаными законами экономии. Прямая и плоскость встречаются в природе исключительно редко, главным образом среди низших форм растений и животных, но человек, пренебрегая более тонкими соображениями, определяющими выбор тех или иных средств в природе, и постоянно совершая ошибки, вынужден достигать своих целей простейшими и наиболее прямыми из доступных ему методов. Поэтому он принимает за единицу длины некий отрезок прямой, за единицу площади — плоскую фигуру, известную под названием квадрата, и за единицу объема — тело, ограниченное шестью гранями и известное под названием куба. Мы видели, что на плоскости квадрат можно построить, перемещая отрезок в перпендикулярном ему направлении на расстояние, равное длине отрезка. Аналогично можно построить и куб в трехмерном пространстве. Представим себе, что квадрат ABА'В' (рис. 3) перемещается па расстояние, равное длине любой из его сторон, в направлении, перпендикулярном плоскости квадрата. В результате такого перемещения мы получим (рис. 7) трехмерную фигуру — куб.

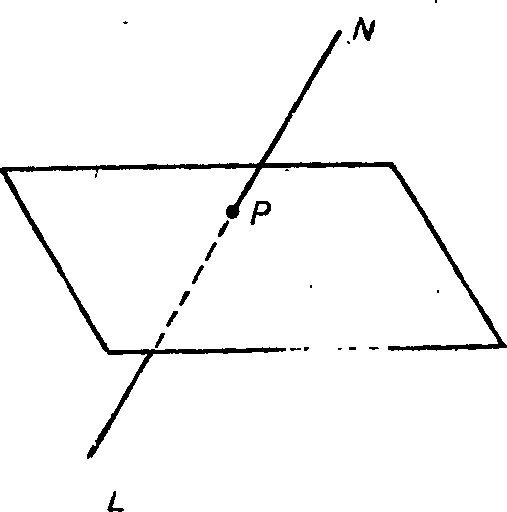
Рис. 6.

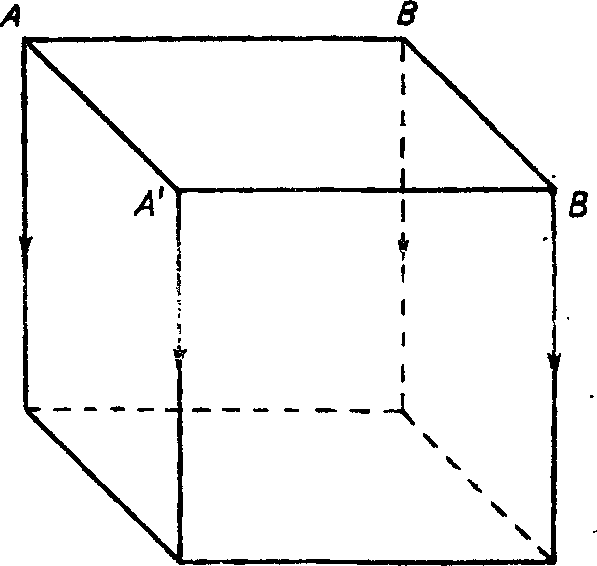
Рис. 7.

Предположим, что исходный отрезок AB, позволивший нам построить квадрат и куб, мы выбрали длиной в два дюйма. Тогда самому отрезку мы могли бы поставить в соответствие число 2, квадрату — число 2?, а кубу — число 2?. Поскольку существуют числа 2?, 2⁵ и т. д„геометрический смысл которых неизвестен, естественно возникает вопрос: не могут ли эти числа соответствовать неким объектам, восприятие которых лежит за гранью человеческих возможностей, но было бы доступно каким-нибудь высшим существам, если бы таковые обладали соответствующими органами чувств? Человеческий разум не в силах наглядно представить себе четырехмерное пространство, в котором могло бы находиться тело, соответствующее числу 2?, но, рассуждая по аналогии, мы в состоянии выяснить несколько интересных фактов относительно фигуры, играющей в четырехмерном пространстве такую же роль, какую в нашем пространстве играет куб.

Мы видели, что: 1) точки ограничивают отрезок прямой; 2) отрезки прямых ограничивают квадрат; 3) квадраты ограничивают куб. Таким образом, в каждом измерении единичная фигура ограничена единичными фигурами на единицу меньшего числа измерений. Следовательно, четырехмерный аналог куба ограничен трехмерными кубами. Строя квадрат, мы передвинули единичный отрезок по кратчайшему пути' из начального положения в конечное, причем длина пути была равна длине самого отрезка. Аналогично куб мы построили, переместив квадрат из начального положения в конечное, отстоящее от начального на расстояние, равное длине стороны квадрата. И в том, и в другом случае движение происходило в направлении, перпендикулярном всем и каждой из границ производящей фигуры.

Отсюда мы заключаем, что и четырехмерный аналог куба можно построить, переместив куб на расстояние, равное длине любого из его ребер, в направлении, перпендикулярном всем ребрам производящего куба. Нашему разуму это направление представляется столь же чуждым и странным, как высота — существу, обитающему в двумерном мире.

При движении отрезка прямой, заметающего квадрат, число границ вновь построенного квадрата было равно удвоенному числу отрезков (исходный отрезок плюс отрезок в конечном положении) плюс два отрезка, порожденные при движении концами исходного отрезка. Аналогично в число граней куба следует включить два квадрата (производящий квадрат в исходном и в конечном положении) плюс четыре квадрата, порожденных при движении четырьмя сторонами исходного квадрата. Отсюда ясно, что в число кубов, ограничивающих четырехмерный аналог куба, должны входить два куба (производящий куб в исходном и в конечном положении) плюс шесть кубов, порожденных при движении гранями исходного куба, то есть всего восемь кубов.

Возвращаясь к квадрату и кубу, нетрудно видеть, что число вершин у построенной фигуры всякий раз оказывается вдвое больше, чем у производящей фигуры. Так, прямолинейный отрезок с двумя конечными точками («вершинами») порождает квадрат с четырьмя вершинами, а у куба число вершин достигает восьми. Следовательно, у четырехмерного аналога куба число вершин равно шестнадцати. Число ребер, или отрезков прямых, соединяющих вершины, можно подсчитать следующим образом. У квадрата четыре стороны («ребра»): две из них образуют производящий отрезок в начальном и конечном состоянии, две другие вычерчивают при движении концы производящего отрезка. У куба двенадцать ребер: восемь из них дает производящий квадрат в исходном и конечном положении, а остальные вычерчивают при движении вершины квадрата. Таким образом, число ребер у каждой фигуры равно удвоенному числу ребер у производящей фигуры плюс те ребра, которые порождают при своем движении вершины производящей фигуры. Следовательно, у четырехмерного аналога куба имеется 12 ? 2 + 8 = 32 ребра. Итак, четырехмерный аналог куба ограничен восемью кубами, шестнадцатью вершинами и тридцатью двумя ребрами. Если ребро производящего куба имеет в длину 2 дюйма, то «объем» четырехмерного куба выразился бы числом 2?.

Сколь ни любопытными могут показаться приведенные выше геометрические утверждения, они меркнут в сравнении с теми драматическими последствиями, к которым приводит понятие четвертого измерения. Для существа, способного воспринимать лишь длину и ширину, прямая, проведенная нами на плоскости, стала бы столь же непреодолимым препятствием, каким служил бы для нас каменный забор, неограниченно простирающийся в высоту. Но это еще не все. Мы, трехмерные существа, можем дотронуться до любой части внутри плоской фигуры, не прикасаясь к ее границе. Представим себе, что на плоскости внутри некоторой замкнутой кривой находятся несколько двумерных существ. Каково бы было их изумление, если бы они узнали, что некие высшие существа обладают способностью проникать сквозь любое известное им ограждение, даже не прикасаясь к нему! Нечто аналогичное можно представить себе и в нашем мире. Предположим, что существо A, запертое в герметически закрытом бронированном сейфе, внезапно обнаруживает рядом с собой некое существо B, спустившееся из четвертого измерения.

Из приведенных выше соображений ясно, что если бы мы обладали способностью перемещаться в четвертом измерении, то могли бы без труда съесть мякоть плода, оставив в неприкосновенности его кожуру, или полакомиться орехом, не разбив его скорлупы. Нам не понадобились бы окна и двери для доступа света и сообщения с внешним миром: четвертое измерение лишило бы былой эффективности стены, пол и потолок, ограждающие наше жилище от внешнего мира.

Развитие наших органов чувств происходит очень медленно и, согласно теории эволюции, зависит от того, в какой мере мы пользуемся ими. Поэтому мы вправе утверждать, что сейчас подошли неизмеримо ближе к восприятию четвертого измерения, чем при возникновении этого понятия.

Отсюда мы заключаем, что и четырехмерный аналог куба можно построить, переместив куб на расстояние, равное длине любого из его ребер, в направлении, перпендикулярном всем ребрам производящего куба. Нашему разуму это направление представляется столь же чуждым и странным, как высота — существу, обитающему в двумерном мире.

При движении отрезка прямой, заметающего квадрат, число границ вновь построенного квадрата было равно удвоенному числу отрезков (исходный отрезок плюс отрезок в конечном положении) плюс два отрезка, порожденные при движении концами исходного отрезка. Аналогично в число граней куба следует включить два квадрата (производящий квадрат в исходном и в конечном положении) плюс четыре квадрата, порожденных при движении четырьмя сторонами исходного квадрата. Отсюда ясно, что в число кубов, ограничивающих четырехмерный аналог куба, должны входить два куба (производящий куб в исходном и в конечном положении) плюс шесть кубов, порожденных при движении гранями исходного куба, то есть всего восемь кубов.

Возвращаясь к квадрату и кубу, нетрудно видеть, что число вершин у построенной фигуры всякий раз оказывается вдвое больше, чем у производящей фигуры. Так, прямолинейный отрезок с двумя конечными точками («вершинами») порождает квадрат с четырьмя вершинами, а у куба число вершин достигает восьми. Следовательно, у четырехмерного аналога куба число вершин равно шестнадцати. Число ребер, или отрезков прямых, соединяющих вершины, можно подсчитать следующим образом. У квадрата четыре стороны («ребра»): две из них образуют производящий отрезок в начальном и конечном состоянии, две другие вычерчивают при движении концы производящего отрезка. У куба двенадцать ребер: восемь из них дает производящий квадрат в исходном и конечном положении, а остальные вычерчивают при движении вершины квадрата. Таким образом, число ребер у каждой фигуры равно удвоенному числу ребер у производящей фигуры плюс те ребра, которые порождают при своем движении вершины производящей фигуры. Следовательно, у четырехмерного аналога куба имеется 12 ? 2 + 8 = 32 ребра. Итак, четырехмерный аналог куба ограничен восемью кубами, шестнадцатью вершинами и тридцатью двумя ребрами. Если ребро производящего куба имеет в длину 2 дюйма, то «объем» четырехмерного куба выразился бы числом 2?.

Сколь ни любопытными могут показаться приведенные выше геометрические утверждения, они меркнут в сравнении с теми драматическими последствиями, к которым приводит понятие четвертого измерения. Для существа, способного воспринимать лишь длину и ширину, прямая, проведенная нами на плоскости, стала бы столь же непреодолимым препятствием, каким служил бы для нас каменный забор, неограниченно простирающийся в высоту. Но это еще не все. Мы, трехмерные существа, можем дотронуться до любой части внутри плоской фигуры, не прикасаясь к ее границе. Представим себе, что на плоскости внутри некоторой замкнутой кривой находятся несколько двумерных существ. Каково бы было их изумление, если бы они узнали, что некие высшие существа обладают способностью проникать сквозь любое известное им ограждение, даже не прикасаясь к нему! Нечто аналогичное можно представить себе и в нашем мире. Предположим, что существо A, запертое в герметически закрытом бронированном сейфе, внезапно обнаруживает рядом с собой некое существо B, спустившееся из четвертого измерения.

Из приведенных выше соображений ясно, что если бы мы обладали способностью перемещаться в четвертом измерении, то могли бы без труда съесть мякоть плода, оставив в неприкосновенности его кожуру, или полакомиться орехом, не разбив его скорлупы. Нам не понадобились бы окна и двери для доступа света и сообщения с внешним миром: четвертое измерение лишило бы былой эффективности стены, пол и потолок, ограждающие наше жилище от внешнего мира.

Развитие наших органов чувств происходит очень медленно и, согласно теории эволюции, зависит от того, в какой мере мы пользуемся ими. Поэтому мы вправе утверждать, что сейчас подошли неизмеримо ближе к восприятию четвертого измерения, чем при возникновении этого понятия.