Мнение и опровержение
Нельзя не увидеть, с какой простотой эти концепции ведут к свойствам, уже известным, и к бесконечному множеству других, которые обычная геометрия с легкостью объяснить не может.
Жан-Виктор Понселе
Первое открытие — проективная геометрия — родилось в суматохе войны. В 1700-е годы Франция, Англия, Австрия, Пруссия, Испания, Нидерланды и другие государства соперничали на европейской арене. Союзы снова и снова возникали и распадались, происходили территориальные стычки из-за колоний, страны стремились к господству в торговле с Новым Светом. Всю первую половину XVIII столетия Франция, Англия и другие страны враждовали, и примерно через четверть века после смерти Ньютона разразилась полномасштабная война. Франция, Австрия, Испания и Россия противостояли Англии и Пруссии.
В 1763 году Франция капитулировала, и Семилетняя война (официальному ее объявлению предшествовали два года сражений) закончилась. Победа сделала Англию преобладающей силой в мире, но далось это дорогой ценой. И Франция, и Англия были истощены и в долгах, следствием этого для обеих стран стали революционные потрясения. Немногим более чем через десятилетие после окончания Семилетней войны началась война за независимость американских колоний, лишившая Англию ее богатейших заморских владений. В 1789 году, как раз когда Джордж Вашингтон возглавил вновь образованные Соединенные Штаты, началась Французская революция. Через четыре года революционеры обезглавили короля Франции.
Математик Гаспар Монж подписал постановление революционного правительства о казни короля. Монж был превосходным геометром, специализировавшимся в стереометрии. Его заслугой было то, как архитекторы и инженеры изображали здания и машины: они создавали проекции сооружений на горизонтальную и вертикальную плоскости, сохраняя таким образом всю информацию, необходимую для создания объекта. Работы Монжа были так важны для армии, что значительная их часть была засекречена сначала революционным, а затем пришедшим ему на смену наполеоновским правительством.
Жан-Виктор Понселе был учеником Монжа, осваивавшим трехмерную геометрию в качестве инженера наполеоновской армии. К своему несчастью, Понселе оказался в армии, как раз когда Наполеон в 1812 году вступил в войну с Россией.
При отступлении от Москвы наполеоновская армия была почти полностью уничтожена жестокой русской зимой и не менее жестокой русской армией. После сражения под Красным Понселе, которого сочли убитым, остался на поле боя. Он был жив и попал в плен к русским. За время пребывания в плену Понселе создал новую дисциплину: проективную геометрию.
Математика Понселе была кульминацией работы, начатой художниками и архитекторами в XV веке — Филиппо Брунеллески и Леонардо да Винчи, которые обнаружили, как рисовать реалистично, используя перспективу. Когда все «параллельные» прямые сходятся в единственной точке на картине, зрителя заставляют верить, что они никогда не встретятся. Квадраты на полу на рисунке делаются трапециями, каждый предмет мягко искажается, но все выглядит совершенно естественным.
Таково свойство бесконечно удаленной точки — ноля в бесконечности.
Иоганн Кеплер, ученый, открывший, что планеты движутся по эллиптическим орбитам, распространил эту идею — идею бесконечно удаленной точки — еще на один шаг вперед. Эллипсы имеют два фокуса; чем более удлиненным является эллипс, тем дальше отстоят друг от друга фокусы. Все эллипсы обладают одним и тем же свойством: если бы у вас оказалось зеркало эллиптической формы и вы поместили в один из фокусов лампочку, все световые лучи сошлись бы в другом фокусе, вне зависимости от того, насколько вытянут был бы эллипс (рис. 29).
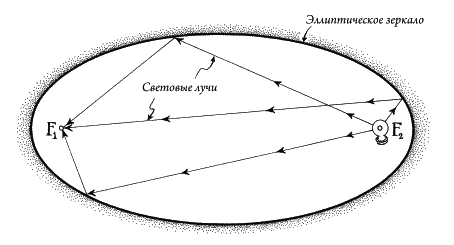
Рис. 29. Световые лучи в эллипсе
Кеплер в уме все больше и больше вытягивал эллипс, удаляя его фокус все дальше. Потом Кеплер вообразил, что второй фокус удален бесконечно далеко: он стал точкой в бесконечности. Неожиданно эллипс превратился в параболу, а все прямые, сходившиеся к точке, сделались параллельными. Парабола — это просто эллипс с одним фокусом в бесконечности (рис. 30).
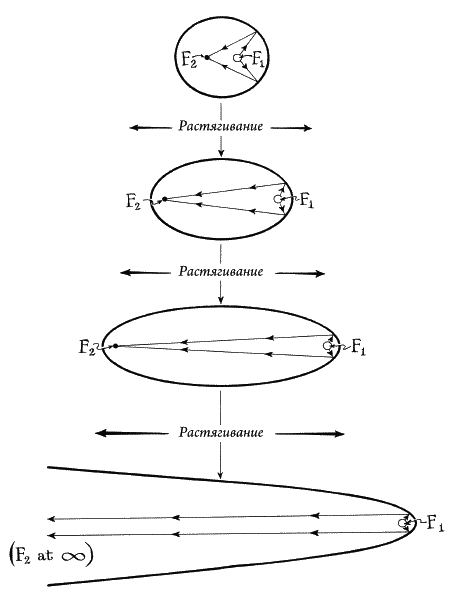
Рис.30. Растягивание эллипса дает параболу
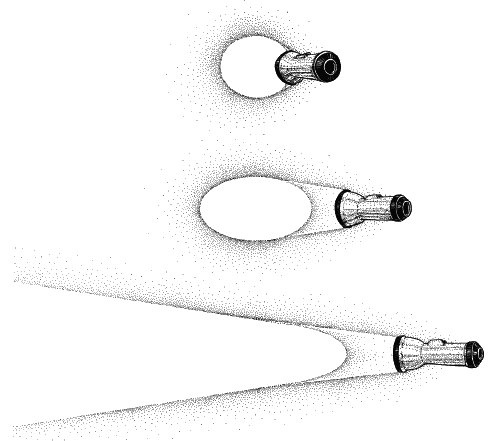
Рис.31. Получение эллипса и параболы с помощью фонарика
Это можно увидеть с помощью фонарика. Войдите в темную комнату и встаньте у стены. Направьте свет фонарика прямо на стену. На стене вы увидите ясный круг света. Теперь медленно наклоняйте фонарик вверх (рис. 31). Вы увидите, что круг растягивается в эллипс, который делается все длиннее и длиннее по мере того как вы увеличиваете наклон. Неожиданно эллипс раскрывается и превращается в параболу. Таким образом кеплеровская бесконечно удаленная точка доказала, что параболы и эллипсы в сущности одно и то же.
Это было началом проективной геометрии, дисциплины, в которой математики рассматривают тени и проекции геометрических фигур, чтобы узнать их скрытые свойства, даже более примечательные, чем родственность парабол и эллипсов. Впрочем, все зависело от того, признавалась ли бесконечно удаленная точка.
Жерар Дезарг, французский архитектор XVII века, был одним из зачинателей проективной геометрии. Он использовал бесконечно удаленную точку для доказательства ряда важных новых теорем, однако коллеги Дезарга не могли понять его терминологии и сочли его сумасшедшим. Хотя некоторые математики, например Блез Паскаль, оценили работы Дезарга, они были забыты.
Для Жана-Виктора Понселе это не имело значения. Как ученик Монжа, Понселе освоил систему построения проекций в двух плоскостях, а будучи военнопленным, имел достаточно свободного времени. Он использовал свое пребывание в плену для того, чтобы заново открыть концепцию бесконечно удаленной точки. Использовав ее для развития идей Монжа, он стал подлинным создателем проективной геометрии. По возвращении из России (он привез с собой счеты — русский абак, к тому времени архаическую диковинку) Понселе поднял проективную геометрию до уровня настоящего высокого искусства[30]. Впрочем, Понселе не имел представления о том, что проективная геометрия раскроет таинственную природу ноля, потому что для этого требовался второй важный прорыв, еще один важный компонент — комплексная плоскость. За этой частью загадки мы должны отправиться в Германию.
Карл Фридрих Гаусс, родившийся в 1777 году, был немецким вундеркиндом. Он начал свою математическую карьеру с исследования мнимых чисел. Его докторская диссертация включала доказательство фундаментальной теоремы алгебры — что полином степени n (квадратное уравнение имеет степень 2, кубическое — 3 и т.д.) имеет n корней. Это верно только в том случае, если вы принимаете мнимые числа, как и вещественные.
За свою жизнь Гаусс исследовал множество проблем, относящихся к самым разным разделам математики над невероятным множеством тем; его исследование работы по теории кривизны стало ключевым компонентом для общей теории относительности Эйнштейна. Кроме того, целую новую структуру в математике создал метод изображения комплексных чисел Гаусса.
В 1830-е годы Гаусс понял, что каждое комплексное число — число, имеющее вещественную и мнимую часть, как 1 — 2i — может быть изображено в декартовых координатах. Горизонтальная ось представляет вещественную часть комплексного числа, а вертикальная — мнимую (рис. 32). Эта простая конструкция, названная комплексной плоскостью, раскрыла многое о том, как работают числа.
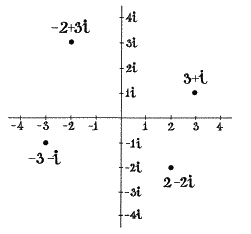
Рис. 32. Комплексная плоскость
Возьмите, например, число i. Угол между ним и осью x составляет 90 градусов (рис. 33). Что произойдет, когда вы возведете i в квадрат? Ну, по определению, i2 = –1. Эта точка отстоит на 180 градусов от оси x: угол удвоился.
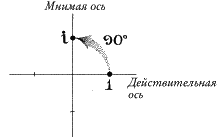
Рис. 33. i под углом 90 градусов
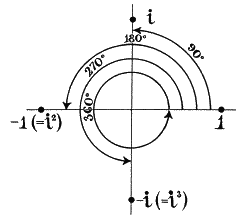
Рис. 34. Различные возможности i
Число i3 равно –i — в 270 градусах от оси x: угол утроился. Число i4 = 1. Мы совершили оборот в 360 градусов — ровно в четыре раза больше исходного угла (рис. 34). Это не совпадение. Возьмите любое комплексное число и измерьте угол. Возведение этого числа в степень n увеличивает угол в n раз. И по мере того как вы все больше и больше увеличиваете n, число по спирали движется внутрь или наружу, в зависимости от того, находится ли исходное число внутри или снаружи единичной окружности — окружности с центром в начале координат и с радиусом 1 (рис. 35).
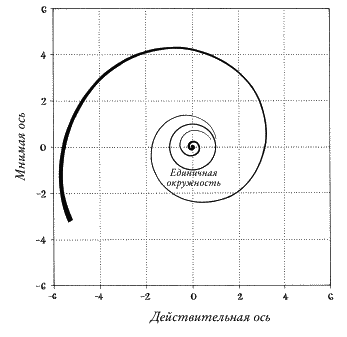
Рис. 35. Спирали внутри и снаружи единичной окружности
Умножение и возведение в степень на комплексной плоскости становятся геометрическими идеями, можно видеть, что происходит. Это было вторым большим продвижением вперед.
Человеком, который объединил эти две идеи, был ученик Гаусса Георг Фридрих Бернхард Риман. Риман объединил проективную геометрию с комплексными числами, и неожиданно прямые превратились в окружности, окружности — в прямые, а ноль и бесконечность стали полюсами шара, полного чисел.
Риман представлял себе прозрачный шар на комплексной плоскости; южный полюс шара касался ноля. Если бы на северном полюсе шара был крошечный источник света, все фигуры, отмеченные на шаре, отбрасывали бы тени на лежащую внизу плоскость. Тень экватора образовывала бы окружность вокруг начала координат. Тень южного полушария находится внутри окружности, а тень северного — снаружи (рис. 36). Начало координат — ноль — совпадает с южным полюсом. Каждая точка на шаре имеет тень на комплексной плоскости; в определенном смысле каждая точка на шаре — эквивалент своей тени на плоскости, и наоборот. Каждая окружность на плоскости есть тень окружности на шаре, и окружность на шаре соответствует окружности на плоскости — за одним исключением.
Рис. 36. Стереографические проекции шара
Если окружность проходит через северный полюс шара, то ее тень больше не окружность, а прямая. Северный полюс подобен бесконечно удаленной точке, как ее представляли себе Кеплер и Понселе. Прямые на плоскости — это просто окружности на сфере, проходящие через северный полюс — бесконечно удаленную точку (рис. 37).
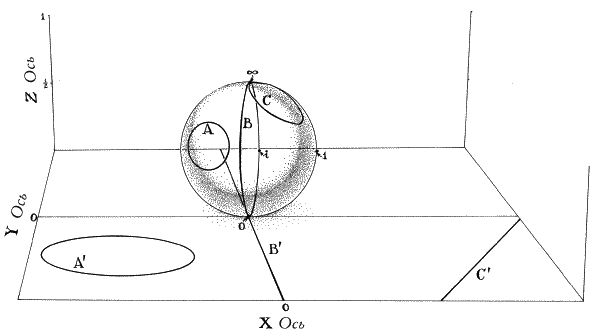
Рис. 37. Прямые и окружности — одно и то же
Как только Риман увидел, что комплексная плоскость (с бесконечно удаленной точкой) — то же самое, что и сфера, математики смогли увидеть умножение, деление и другие, более трудные операции, анализируя, как деформируется и вращается сфера. Например, умножение на число i эквивалентно вращению сферы на 90 градусов по часовой стрелке. Если вы берете число x и заменяете его на (x — 1)/(x + 1), это эквивалентно такому повороту всей сферы на 90 градусов, что северный и южный полюса оказываются на экваторе (рис. 38, 39, 40). Самое интересное, что если вы берете число x и заменяете его на обратную величину 1 / x, это эквивалентно перевороту всей сферы вверх ногами и зеркальному отражению. Северный полюс становится южным, а южный — северным, ноль становится бесконечностью, а бесконечность — нолем. Все это встроено в геометрию сферы, 1 / 0 = ? и 1 /? = 0. Бесконечность и ноль — просто противоположные полюса сферы Римана и могут мгновенно меняться местами. Они имеют равные и противоположные силы.
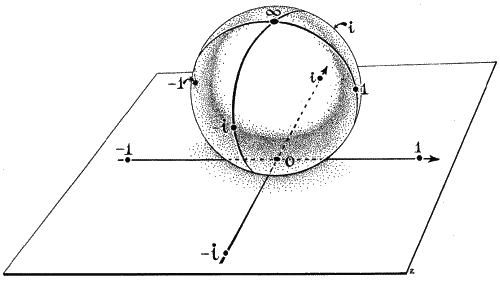
Рис. 38. Сфера Римана
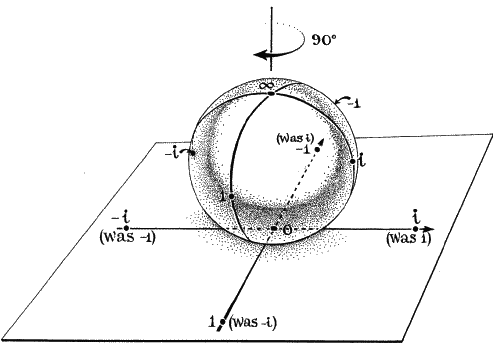
Рис. 39. Сфера Римана, трансформированная i
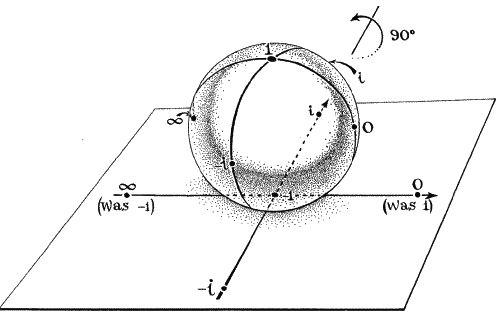
Рис. 40. Сфера Римана, трансформированная (x — 1)(x + 1)
Возьмите все числа на комплексной плоскости и умножьте на 2. Похоже, что вы взялись рукой за южный полюс и растянули резиновое покрытие сферы от южного к северному полюсу. Умножение на 1/2 произведет обратный эффект: как будто вы растянули резиновое покрытие от северного полюса к южному. Умножение на бесконечность подобно втыканию иглы в южный полюс: резиновое покрытие все стянется вверх, к северному полюсу: любое число, умноженное на бесконечность, есть бесконечность. Умножение на ноль подобно втыканию иглы в северный полюс, и все стягивается к нолю: любое число, умноженное на ноль, есть ноль. Бесконечность и ноль равны и противоположны и одинаково разрушительны.
Ноль и бесконечность вечно борются за поглощение всех чисел. Как в манихейском кошмаре, эти двое сидят на противоположных полюсах числовой сферы, всасывая в себя числа, как маленькие черные дыры. Возьмите любое число на плоскости. Для примера пусть это будет i / 2. Возведем его в квадрат, в куб, в четвертую степень, в пятую, шестую, седьмую степень… Продолжаем умножать. Числа медленно по спирали приближаются к нолю, как вода по трубе. Что произойдет с 2i? В точности противоположное. Возведем его в квадрат, в куб, в четвертую степень… Числа по спирали устремятся вовне (рис. 41). Однако на числовой сфере эти две кривые — дубликаты друг друга, они — зеркальные отражения (рис. 42). Такова судьба всех чисел на комплексной плоскости. Они неизбежно притягиваются к нолю или к бесконечности. Единственные числа, которые избегают этой участи, — те, что равноудалены от соперников, числа на экваторе, такие как 1, –1 и i. Эти числа, с одинаковой силой притягиваемые и нолем, и бесконечностью, вечно двигаются по спирали на экваторе и не могут вырваться. (Вы можете увидеть это на своем калькуляторе. Введите число — любое число. Возведите его в квадрат. Результат снова возведите в квадрат. Делайте это снова и снова. Последовательность быстро устремится к бесконечности или к нолю, если только вы изначально не ввели 1 или –1. Избавления нет.)
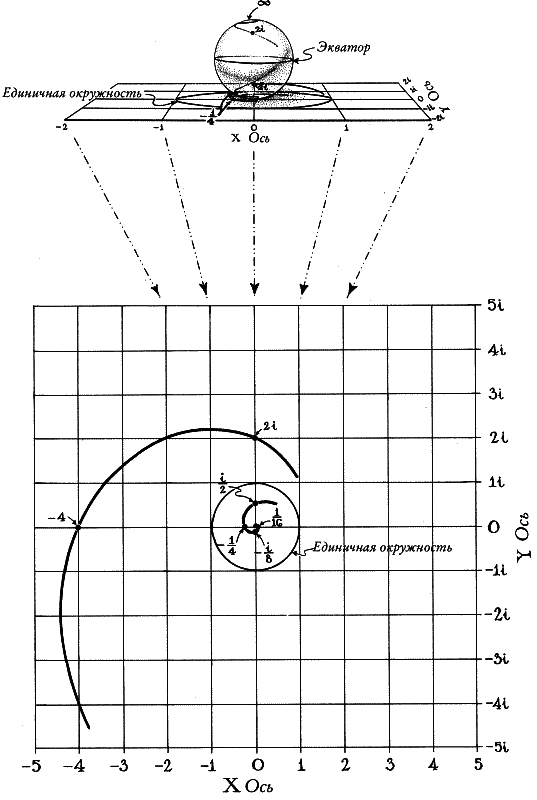
Рис. 41. Спиральное движение вовне и внутрь на плоскости
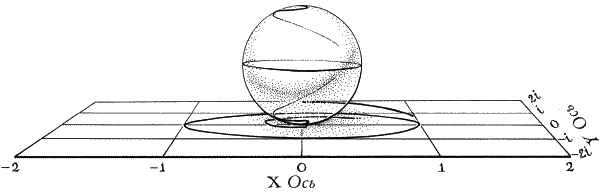
Рис. 42. На сфере — зеркальное отражение
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК