ПО СЛЕДАМ РУАНСКИХ ВПЕЧАТЛЕНИЙ
ПО СЛЕДАМ РУАНСКИХ ВПЕЧАТЛЕНИЙ
— Хорошо! — разнеженно вздыхает Фило, глядя влюбленными глазами на Асмодея, который шумно лакает чай из старинной чашки в форме лилии. — Налить вам еще?
— Не откажусь, мсье. Такой чай! Да еще из такой чашки…
— Вам она нравится?
— Очень, мсье. Особенно рисунки в стиле Ватто.[74]
Фило и Мате знают эти рисунки наизусть (на одном из них кукольно улыбающаяся пастушка в фижмах надевает ленточку на шею прелестному ягненку; на другом столь же кукольно улыбающийся пастушок надевает колечко на палец все той же пастушке). Но похвала Асмодея заставляет их все же бросить беглый взгляд на тот рисунок, который приходится каждому перед глазами. И тут они вдруг замечают, что изображена на нем совсем другая, хоть и знакомая сцена: юноша с разметавшимися волосами лежит на широкой деревянной кровати. Девушка с оспинками на лице опадет ему салфетку на лоб.
— Что это, Асмодей?
Тот, по обыкновению, невинно опускает глазки.
— Ничего особенного, мсье. Надо же мне как-то вернуть вас к прерванной работе!
И разговор снова возвращается к эпизоду «Арифметическая машина Паскаля».
Мате сожалеет, что самой машины так и не видал. Ну да ничего не поделаешь! Ведь во время их пребывания в Руане она еще не была готова. К тому же сейчас, в двадцатом столетии, изобретение это представляет интерес чисто исторический…
— До известной степени, мсье, — возражает бес. — Творец кибернетики Норберт Винер, например, справедливо отмечает, что машина Паскаля имеет самое непосредственное отношение к настольным арифмометрам современного образца. Ведь в основу ее устройства положен часовой механизм, а часовые механизмы используются в ручных арифмометрах и поныне.
Асмодей запихивает в рот громадный кусок яблочного пирога и, мигом разделавшись с ним, продолжает:
— Между прочим, то, что Паскаль прибег к зубчатой передаче, едва ли не самое главное его достижение. Тем самым поступательное движение, которое используется, скажем, в русских и китайских счетах, он заменил вращательным. Притом так, что перенос десятков в следующий разряд происходит автоматически. Когда в числовом разряде накапливается десять единиц, они с помощью специального рычажка заменяются нулем, а к цифре следующего разряда прибавляется единица. И принцип этот, кстати сказать, сохраняется не только в арифмометрах, но и во многих измерительных приборах. В счетчиках такси, в электросчетчиках…
— Представляю себе, как обрадовались бухгалтеры семнадцатого века, когда счетная машина была наконец завершена! — фантазирует Фило.
— Кха, кха… Не думаю, чтобы очень, мсье. К сожалению, она была слишком дорога для них. Да и в работе сложновата. К тому же частенько портилась. Тогда ведь не умели еще устранять трение. Отсюда вечные заедания, зацепки…
— Хоть бы и так, — хорохорится Фило, — а все-таки четыре действия арифметики с плеч долой!
— Не четыре, а только два, мсье. Сложение и вычитание. Арифмометр Паскаля — прародитель так называемых сумматорных машин. Зато уже спустя каких-нибудь два-три десятилетия появилась сумматорно-множительная машина Лейбница.
— Последователь, стало быть, не заставил себя ждать.
— Не последователь, а последователи, — снова поправляет бес. — Даже в семнадцатом веке их уже было несколько. Само собой, охотники погреть руки на чужом таланте — не в счет. Паскаля оградила от них королевская привилегия, а еще — их собственное невежество: изготовление мало-мальски сносной подделки требовало сноровки и знаний, которых у них не было. Ну да что о них толковать! Мы ведь говорим о связи машины Паскаля с современностью.
— Как? Разве разговор не закончен? — удивляется Мате.
— Нет, мсье, мы как раз подошли к самому главному. А главное для нас с вами — отнюдь не устройство машины, а идея. Да, да, идея, которая подтолкнула мсье Паскаля к ее созданию. Он, если помните, руководствовался утверждением Декарта, полагавшего, что мозгу человеческому свойствен некий автоматизм и что многие умственные процессы, по сути дела, ничем не отличаются от механических. Иными словами, мозг столько же автомат, сколько живой орган. Долгие годы работы заставили Паскаля не только утвердиться в этой мысли, но и углубить ее. Он понял, что действия арифметической машины даже ближе к мыслительному процессу, нежели то, на что способен живой мозг…
— Что?! — взвивается Мате. — У Паскаля есть такая запись? Но ведь это же одно из тех положений, на которых основана кибернетика!
— В том-то и дело, мсье! И значит, у нас с вами есть все основания считать Паскаля ее отдаленным предшественником, что совершенно необходимо отметить еще одной чашкой чая.
Хозяин, улыбаясь, принимает у черта пустую чашку. Но что это? Рисунок на ней опять изменился! Теперь там изображены они сами — Фило, Мате и Асмодей в своем маркизовом обличье, восседающие на крыше руанской судебной палаты.
Улыбка медленно сползает с круглой физиономии Фило. Неужели его заставят копаться в теореме Дезарга? К счастью, эта неприятная для него операция переносится на другое время. Зато разговор о своей собственной теореме Мате откладывать не намерен. И многострадальный филолог покоряется своей участи.
— Итак, — говорит Мате, — напоминаю суть теоремы. Если на сторонах произвольного треугольника построить снаружи или внутри (значения не имеет) по равностороннему треугольнику и соединить прямыми их центры тяжести, то полученный таким образом новый треугольник тоже будет равносторонним.
— Насколько я понимаю, именно это и нуждается в доказательстве, — капризно замечает Фило.
— Совершенно верно. Какого рода доказательство вы желаете получить? Общее или частное — на числовом примере?
— Достаточно будет и частного!
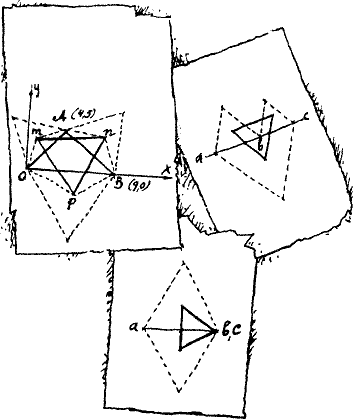
— Понятно, — ядовито кивает Мате. — Тогда к общему виду потрудитесь привести его самостоятельно. А теперь вычертим произвольный треугольник и выберем систему координат с началом в одной из вершин треугольника. Скажем, в точке О. Ось иксов направим вдоль стороны ОВ. — Говоря это, Мате набрасывает чертеж в своем неизменном блокноте. — Как видите, координаты вершины О — нуль, нуль; вершины А — четыре, пять; вершины В — девять, нуль. Теперь нетрудно вычислить и размеры сторон треугольника.
— По известной формуле, — сейчас же соображает Асмодей. — Квадрат расстояния между двумя точками равен сумме квадратов разностей координат этих точек, иначе говоря
d2 = (X1 — Х2)2 + (У1 — У2)2.
— Очень хорошо. Подставим в эту формулу координаты соответствующих вершин треугольника. Тогда:
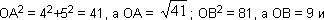
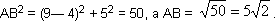
Ну, а теперь построим на сторонах нашего треугольника новые треугольники, на сей раз равносторонние. Намечаю их пунктиром. Буквами n, m и р обозначим точки пересечения медиан в каждом из них. Это и будут их центры тяжести. Точки эти, как известно, находятся на расстоянии двух третей медианы, считая от вершины. В первом равностороннем треугольнике это Am = От. Во втором — An = Вn. В третьем — Вр = Ор. Но так как в равностороннем треугольнике медианы являются в то же время и высотами, а высота в этом случае равна половине стороны, умноженной на
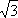
то
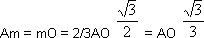
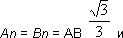

Иначе:
(Ат)2 = (mO)2 = (AO)2/3 = 41/3, (An)2 = (Вn)2 = AB2/3 = 50/3;
(Вр)2 = (Ор)2 = OB2/3 = 27.
Мате на мгновение отрывается от чертежа и, убедившись, что Фило еще жив, продолжает:
— Далее обозначим искомые координаты центров тяжести равносторонних треугольников. Точки m: х1, у1; точки n: x2, у2; точки р: х3, у3. Займемся сперва одним треугольником и по известной уже нам формуле о квадрате расстояния между двумя точками вычислим, что
(Am)2 = (Оm)2 = (x1 — 4)2 + (y1 — 5)2 = x12 + y12 = 41/3.
Решая систему двух уравнений:
(x1 — 4)2 + (y1 — 5)2 = x12 + y12 и x12 + y12 = 41/3, найдем, что
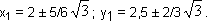
— А как это у вас получилось? — неожиданно для себя самого интересуется Фило.
— По-моему, это понятно всякому школьнику, — сердито отвечает Мате.
— Допустим. А как же быть с двумя знаками перед вторыми слагаемыми? Какой из них выбрать?
— Ну, а это уж где как. Обратите внимание на то, что первые слагаемые (2 и 2,5) — это координаты середины стороны ОА. В самом деле:
(O + 4)/2 = 2 и (O + 5)/2 = 2,5
А точка т лежит слева от этой середины, но выше ее. Следовательно, в первом равенстве (x1) надо сохранить знак минус, а во втором (у1) — знак плюс. Поэтому окончательно:
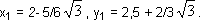
Точно таким же образом найдем координаты точек n и р:
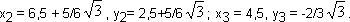
Остается вычислить расстояния между т и п, п и р, р и т. Обозначим их буквой dс соответствующими индексами: тп, пр и рт. Тогда:
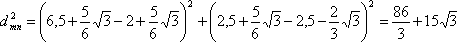
Если теперь вычислить
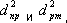
окажется, что все три результата одинаковы:
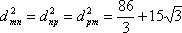
Ну, а раз равны квадраты расстояний, то равны и сами расстояния. Стало быть, соединив точки m, n и р, мы получим равносторонний треугольник.
— Квод демонстрандум эрат! Что и требовалось доказать, — торжественно заключает Асмодей.
— Не забудьте рассмотреть еще два частных случая первоначального треугольника, — суетливо напоминает Мате. — Когда сумма двух сторон равна третьей и когда одна из сторон равна нулю. — Он протягивает Фило и Асмодею заранее заготовленные чертежики. — Как видите, моя теорема справедлива также и для них.
— Благодарю вас, мсье! Поверьте, мне было чрезвычайно интересно! Поздравляю с удачей! — рассыпается бес, но вдруг совершенно неожиданно зевает и страшно смущается. — Пардон, мсье! Не подумайте, что это от вашей теоремы. Всему виной чай. Он всегда действует на меня, как снотворное. С вашего разрешения я вздремну немножко…
Он взлетает на верхнюю полку и скрывается в книге Лесажа, с силой захлопнув за собой картонную обложку. В ту же минуту оттуда начинает исходить легкое блаженное похрапывание: «Хрр-фью… хрр-фью…»
Филоматики растроганно переглядываются.
— Перерыв?
— Перерыв!
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК