Решения

19.1. Лучше отсчитать 25 конвертов, тогда в пачке их останется 75.

19.2. Можно отмерить небольшую стопку листов, скажем высотой 1 см, и сосчитать количество листов в ней, а затем измерить высоту данной стопки и найти число листов в ней из соответствующей пропорции.

19.3. Перед просмотром анкет на листе бумаги заводят по одной колонке для регистрации каждого отдельного вида данных, подлежащих сбору. Затем при считывании этих данных с анкет в соответствующие колонки вносятся специальные значки (палочки, точки и т. п.), а по окончании этой работы производится подсчет количества значков в каждой колонке. Один из наиболее удобных способов регистрации состоит в группировании вносимых значков по 10 штук в виде фигуры, изображенной на рис. 146.

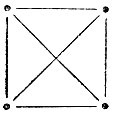
Рис. 146

19.4. Достаточно сосчитать количество гвоздей, скажем, в 100 г или в 1 кг, а затем взвесить ящик с гвоздями (разумеется, вес пустого ящика нужно вычесть) и произвести соответствующие выкладки.

19.5. Вы были в командировке 31 - 23 = 8 дней.

19.6. Из первого пакета во второй нужно переложить 5 конфет, тогда в первом пакете станет на 5 конфет меньше, чем было, а во втором - на 5 конфет больше, чем было.

19.7. Выгоднее пилить более короткие бревна, поскольку отношение числа распилов к числу получаемых кусков для короткого бревна меньше, чем для длинного. Так, для получения 12 кусков из трехметровых беревен нужно сделать 8 распилов, а из четырехметровых - 9 распилов.

19.8. Для подъема на 16-й этаж нужно преодолеть 15 расстояний между этажами, что в 5 раз больше количества таких же расстояний для подъема на 4-й этаж.

19.9. Квартира 165 находится в третьем подъезде на 10-м этаже, так как 165 = 41*4 + 1 = 2*16*4 + 9*4 + 1.

19.10. Две половины порции бульона с пирожками стоят 46 коп. Они составляют полную порцию и еще пирожок, значит, пирожок стоит 46 - 31 = 15 коп.

19.11. Можно выпить 8 бутылок лимонада, при этом останется 20 коп.

19.12. Достаточно расклепать 2 звена, составляющих один обрывок, и с их помощью соединить друг с другом оставшиеся три обрывка.

19.13. Каждый из инженеров может врезать в сейф свой личный замок, ключ от которого есть только у него. Тогда без него открыть сейф будет невозможно.

19.14. На рис. 147 изображен возможный способ использования трех замков с соблюдением условия задачи.

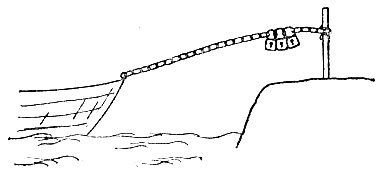
Рис. 147

19.15. Попробовав не более 9 ключей, вы установите, который из 10 ключей подходит к первой двери. Затем, попробовав не более 8 ключей, вы подберете ключ ко второй двери и т. д. Всего вам понадобится не более 9 + 8 + ... + 1 = 45 попыток.

19.16. Достаточно взять 3 носка, так как 2 из них обязательно будут одинакового цвета.

19.17. Для того чтобы наверняка обеспечить пару одноцветных перчаток, нужно взять минимум 11 перчаток: 6 из них обязательно будут одинакового цвета, а среди них, в свою очередь, 2 обязательно придутся на разные руки.

19.18. Можно надеть сразу обе пары перчаток и работать с первым реактивом, затем снять одну пару перчаток и работать со вторым реактивом, наконец, снова надеть снятую пару, вывернув ее наизнанку, и работать с последним реактивом. (В решении, конечно, содержится элемент шутки, так как вряд ли можно снимать, надевать и вывертывать "грязные" перчатки, не испачкав их "чистую" сторону.)

19.19. Достаточно отложить на веревке 3 одинаковых расстояния, потом еще 4 и еще 5 таких расстояний, получив в итоге на веревке 4 отметины. Если теперь соединить начальную и конечную отметины, а оставшиеся 2 отметины оттянуть так, чтобы образовался треугольник, то этот треугольник обязательно будет прямоугольным.

19.20. Один из возможных способов завязывания узла показан на рис. 148.

Рис. 148

19.21. Один из возможных способов прострочить первую эмблему показан на рис. 149. Что же касается второй эмблемы, то ее прострочить с соблюдением условий задачи невозможно.

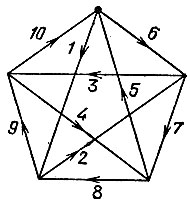
Рис. 149

19.22. Каркас куба содержит 12 ребер, но, чтобы обойти весь этот каркас не прерывая движения, необходимо дополнительно пройти как минимум по трем ребрам. Поэтому для изготовления каркаса указанного куба меньше 1,5 м проволоки будет недостаточно.

19.23. Достаточно разрезать 3 яблока пополам и 2 яблока на 3 части каждое. Получится 6 половинок и 6 третей, которые можно поровну распределить на 6 человек.

19.24. Двумя прямыми разрезами квадратный или круглый торт делим на четыре равные части, а третьим разрезом отсекаем от каких-то двух противоположных частей по одной трети (на рис. 150 цифрами 1, 2, 3 соответственно обозначены части, предназначенные разным людям, если их трое).

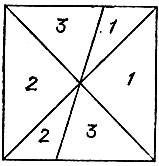
Рис. 150

19.25. Любой торт, однородный по составу, можно разделить на восемь равных частей, если двумя вертикальными разрезами разделить его на 4 равные части, а затем горизонтальным разрезом разделить каждую часть пополам (рис. 151).

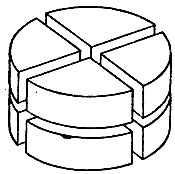
Рис. 151

19.26. Достаточно перегнуть кусок материи пополам, затем одну из половинок перегнуть еще раз пополам и, наконец, ту четвертинку, которая ближе к середине, снова перегнуть пополам. Последняя линия сгиба разделит длину куска в отношении 3:5.

19.27. После стирки от 1 м (длины) материи останется 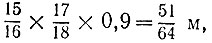поэтому нужно купить 64 м материи.

19.28. Оставшийся после стирки кусок составляет 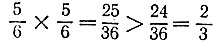первоначального объема. Поэтому его хватит еще на 2 стирки.

19.29. Оба языка знают 50% жителей, поскольку из 80% знающих английских язык 30% не знают французского языка (предполагается, что каждый житель знает хотя бы один из двух названных языков).

19.30. Новые цены составляют ⁴/₅ старых; следовательно, товаров на отведенную сумму можно купить в ⁵/₄ раза, т. е. на 25%, больше.

19.31. Так как для искомой суммы х рублей справедливо неравенство х + 0,02х ≤ 100, то 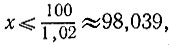а значит, имея 100 рублей, можно перевести максимум 98 рублей 3 копейки.

19.32. Выгоднее купить большой арбуз, так как его объем в 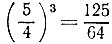раза (т. е. почти в два, а не в полтора) больше, чем объем другого арбуза.

19.33. Выгоднее покупать крупные мандарины, поскольку при увеличении радиуса мандарина площадь его поверхности (пропорциональная квадрату радиуса) увеличивается не так значительно, как его объем (пропорциональный кубу радиуса).

19.34. Площадь поверхности у одного килограмма крупной картошки меньше, чем у того же количества мелкой. Поэтому крупную картошку чистить выгоднее: и быстрее и экономнее (меньше отходов).

19.35. Было отпито ⁷/₈ исходного количества сока, так как из соображений подобия объем оставшейся части сока составляет 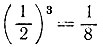прежнего.

19.36. Широкая кружка более вместительна, так как площадь ее основания в 1,5² = 2,25 раза больше площади основания другой кружки, а объем соответственно больше в ^2,25/₂ = 1,125 раза.

19.37. Будем наклонять кружку в точности до тех пор, пока не появится краешек дна (рис. 152). Тогда в кружке останется ровно полкружки молока.

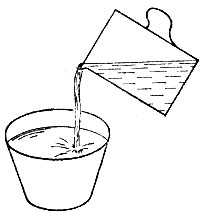
Рис. 152

19.38. Во-первых, из полной кюветы можно отлить ровно половину (рис. 153).

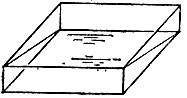
Рис. 153

Во-вторых, можно отлить из кюветы столько воды, чтобы осталась ровно шестая часть кюветы (рис. 154).

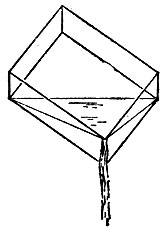
Рис. 154

В-третьих, при наличии какого-либо сосуда для временного хранения воды можно комбинировать также и другие порции воды, кратные шестой части кюветы:

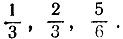
19.39. Измеряем диаметр d основания (внутренний, с учетом толщины стекла) и высоту h₁ столба жидкости, а

затем перевертываем бутылку горлышком вниз и измеряем высоту h₂ столба воздуха в бутылке рис. 155. Теперь остается произвести подсчет

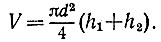
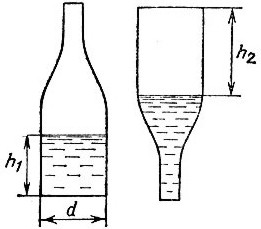
Рис. 155

19.40. Опустим предмет, например, в банку и нальем в нее воды так, чтобы предмет был полностью покрыт водой. Затем, вынув предмет из банки, измерим, на сколько понизится при этом уровень воды. Объем предмета будет равен произведению полученной величины на площадь сечения банки.

19.41. Достаточно поделить объем израсходованной краски на площадь окрашенной поверхности.

19.42. Это можно сделать за четыре операции, результаты которых указаны в следующей таблице (сами операции без труда угадываются по данным таблицы):

19.43. Для выполнения поставленной задачи необходимо сделать минимум 9 переливаний, результаты которых оформлены в виде следующей таблицы:

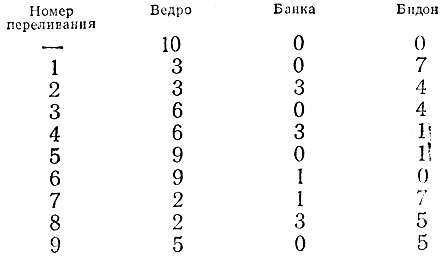
19.44. Достаточно четырех взвешиваний. Сначала взвешиваем 1 кг песку, затем еще 2 кг (положив на одну чашку весов уже взвешенный песок и гирю), затем еще 3 кг (сложив на одной чашке 1 + 2 = 3 кг взвешенного песка) и, наконец, еще 7 кг (сложив на одной чашке весь песок и гирю). Меньшим числом взвешиваниями обойтись нельзя, так как за три взвешивания можно набрать максимум 1 + 2 + 4 = 7 кг песку.

19.45. Если гири можно класть только на одну чашку весов, то необходимо иметь, как минимум, четыре гири. Годится, например, набор гирь в 1, 2, 4, 8 кг. Если же разрешить класть гири на обе чашки, то необходимо иметь три гири. Так, из трех гирь в 1, 3, 9 кг можно скомбинировать любой вес от 1 до 13 кг.

19.46. Для того чтобы взвесить мелкий предмет на грубых весах, нужно увеличить вес этого предмета в достаточное число раз. В нашем случае можно взвесить, скажем, 100 монет по 1 копейке, а затем полученный вес поделить на 100. Полезно знать, однако, что вес копейки равен 1 г.

19.47. а) Три предмета можно упорядочить тремя сравнениями: каждый предмет сравнить с каждым.

б) Для четырех предметов достаточно пяти сравнений: тремя сравнениями упорядочиваются некоторые три предмета, а затем со средним из них сравнивается четвертый предмет, который в зависимости от результата сравнивается, наконец, с одним из двух оставшихся предметов тройки.

в) Пять предметов можно упорядочить семью сравнениями: сначала упорядочим предметы в некоторых двух парах и сравним два более тяжелых предмета по одному из каждой пары, в образовавшуюся при этом тройку вставим пятый предмет, а затем и более легкий предмет оставшейся пары. На все это уйдет не более семи сравнений. Шести сравнений будет, вообще говоря, недостаточно.

19.48. Например, годится следующая формула:

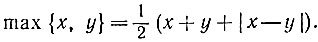
19.49. Достаточно сделать 5 поездок, так как за каждую поездку, кроме последней, можно увезти не менее 2 т. Меньше 5 поездок может не хватить, например, если весь груз расфасовать поровну в 13 ящиков.

19.50. Когда весы находятся в равновесии, отношение весов грузов, лежащих на чашках, есть фиксированная (обратная отношению плеч) величина а. Поэтому если отвесить по 1 кг сахара на каждой чашке весов, то на самом деле будет получено а + ¹/_а кг, что при а≠1 будет больше 2 кг. Чтобы отвесить ровно 2 кг сахара, достаточно весы с килограммовой гирей на одной чашке уравновесить любым грузом (например, тем же песком), а затем снять гирю и уравновесить весы сахаром. Мы получим ровно 1 кг сахара и аналогично еще 1 кг.

19.51. Если прикрепить гирю к одному концу линейки, а взвешиваемый груз к другому (рис. 156) и уравновесить

эту систему, правильно подобрав на линейке точку опоры, то отношение х:y расстояний по линейке от опоры до гири и до груза будет равно отношению весов груза и гири соответственно. Кстати, можно проградуировать линейку, написав возле нескольких возможных положений опоры заранее подсчитанные соответствующие веса груза.

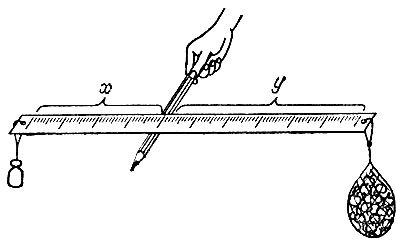
Рис. 156

19.52. Запомнив время на стенных часах, сходите и узнайте правильное время. Вернувшись домой, определите по стенным часам время вашего отсутствия и прибавьте половину этого времени к тому времени, которое вы видели на правильных часах. Это время и нужно установить на ваших часах.

19.53. Время t работы будет наименьшим, если обе машинистки закончат печатать одновременно, т. е. если первая машинистка напечатает ^t/₆ листов, а вторая ^t/₁₀ листов. Поэтому работу между ними нужно заранее распределить в пропорции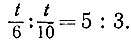

19.54. Если шины на передних колесах стираются за n км пути, а задние - за m км, то перестановка местами передних колес с задними после прохождения 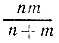км пути приводит к одновременному стиранию всех колес и максимально удлиняет пробег автомобиля без замены шин.

19.55. В результате внедрения всех трех изобретений производственные затраты могут составить минимум 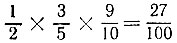прежних затрат. Поэтому они уменьшатся в лучшем случае на 73% (это если сами изобретения оказывают влияние на процесс производства не зависимым друг от друга образом).

19.56. Постоянно на лугу могут пастись максимум 15 коров. Если обозначить через х полное количество травы на лугу, а через y и z количества травы, вырастающей ежедневно на лугу и съедаемой одной коровой за один день соответственно, то будет справедлива система

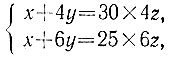
откуда 15z = y. Таким образом, трава на лугу растет с той же скоростью, с какой ее поедают 15 коров. Проверка показывает, что 16 коров съедят всю траву за 60 дней.

19.57. Парашютист мог обойти стену, все время держась за нее, скажем, левой рукой и замеряя углы поворотов, которые ему приходилось при этом делать. Подсчитав в конце алгебраическую сумму всех этих углов (со знаком плюс, если поворот был левым, и со знаком минус, если правым), он мог воспользоваться следующим фактом: сумма углов должна равняться либо -360°, если он находится внутри участка, либо 360°, если снаружи.

19.58. Если поворачивать табуретку в "плоскости" пола, то обязательно наступит такой момент, когда все 4 ножки табуретки будут касаться пола.

19.59. На рис. 157 показано, как, положив кирпич на угол стола, а затем передвинув его параллельно краю стола на длину соответствующего ребра кирпича, можно получить две точки (угол стола и вершина кирпича), расстояние между которыми как раз равно длине главной диагонали кирпича.

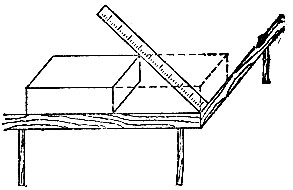
Рис. 157

19.60. Намотаем проволоку в один слой, например, на саму линейку так, чтобы соседние витки проволоки были плотно прижаты друг к другу (рис. 158). Тогда, поделив ширину полученного слоя на количество витков, мы получим толщину одного витка, которая совпадает с диаметром проволоки.

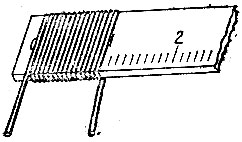
Рис. 158

19.61. Измерим внешний радиус R и внутренний радиус r рулона (рис. 159). Затем отмотаем такую часть ленты длиною l, чтобы при этом ощутимо уменьшился внешний радиус рулона. Если он уменьшился на d, то длина ленты приблизительно равна

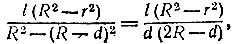
так как длина ленты в рулоне пропорциональна площади его поперечного сечения.

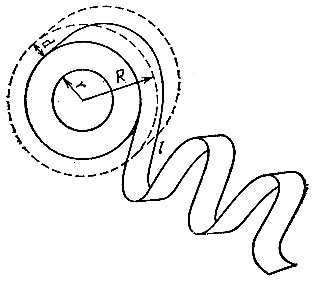
Рис. 159

19.62. Если на осколке сохранились хотя бы три точки края пластинки, то можно перенести их на бумагу и построить центр О окружности, проходящей через эти три точки (рис. 160). Радиус R этой окружности совпадает с радиусом пластинки. Впрочем, его можно и посчитать, измерив, скажем, попарные расстояния a, b и с между тремя указанными точками и воспользовавшись формулами

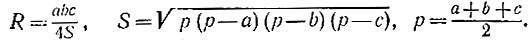
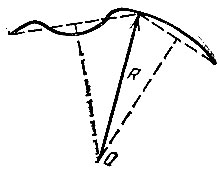
Рис. 160

19.63. Измерим длину l большой окружности шара, образовав из измерительной ленты наименьшее кольцо, через которое проходит шар. Тогда объем шара будет равен ^l3/_(6π²).

19.64. Если обозначить через H высоту маяка, а через R радиус Земли (R ≈ 6400 км), то искомое расстояние будет равно (рис. 161)

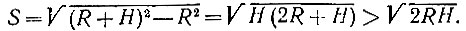
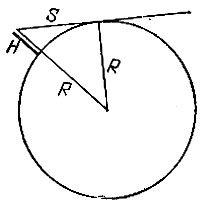
Рис. 161

При H = 125 м имеем S ≈ 40 км.

19.65. Возьмем две точки A и В на поверхности бильярдного шара и проведем на нем дуги равных радиусов с центрами в этих точках. В пересечении дуг получатся точки С и D, аналогично построим точку Е (рис. 162). Теперь, замерив циркулем длины отрезков CD, DE и СЕ, мы перенесем эти точки на бумагу с сохранением указанных длин и построим на бумаге центр О окружности, описанной вокруг получившегося треугольника. Радиус шара как раз и будет равен радиусу этой окружности.

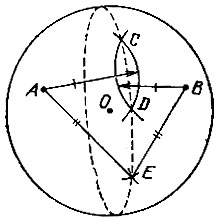
Рис. 162

19.66. Из всех прямоугольников фиксированного периметра наибольшую площадь имеет квадрат, так как величина площади прямоугольника размером а*(з - а) достигает наибольшего значения 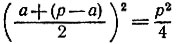при а = p - а.

19.67. Наибольшую площадь будет иметь палисадник, представляющий собой половину квадратного участка, т. е. имеющий две короткие стороны, равные половине длинной стороны, противолежащей стене дома.

19.68. Наибольший объем будет иметь коробка, высота h которой равна четверти стороны основания, поскольку учетверенный объем 4h(a - 2h)² коробки, сделанной из квадрата со стороной а, достигает наибольшего значения

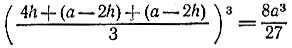
при 4h = a - 2h.

19.69. Если х, y и z - соответственно высота, ширина и длина коробка объемом V, то расход материала на его изготовление пропорционален величине 2xy + 3yz + 4xz, которая принимает наименьшее значение

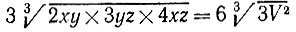
при 2xy = 3yz = 4xz, т. е. когда х:y:z = 3:4:2.

19.70. Кратчайший путь от лампочки А до выключателя В будет равен 40 м и пройдет он не только по потолку и торцевым стенкам (такой путь АВ₁ на развертке, изображенной на рис. 163, имеет длину 42 м), а также и по боковой стене (соответствующий путь на рис. 163 проходит по отрезку АВ₂).

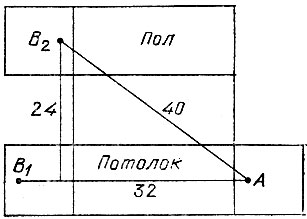
Рис. 163

19.71. Кратчайший путь от лампочки А до выключателя В имеет длину 5 м и показан на развертке бункера (рис. 164).

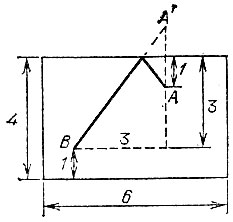
Рис. 164

19.72. Если разместить развертку пяти граней куба так, как изображено на рис. 165, то в четырех углах квадратной салфетки останутся четыре треугольника, которых будет достаточно для покрытия шестой грани куба (подсчет показывает, что нарисованный "крест" действительно помещается в квадрате и даже оставляет зазор шириной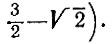

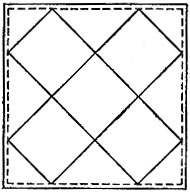
Рис. 165

19.73. Одна из вершин прямоугольника должна совпадать с серединой гипотенузы.

19.74. Через точку А, расположенную от вершины В угла вдвое дальше, чем данная точка С (рис. 166), проведем прямую, параллельную стороне угла. Она пересечет другую сторону угла в точке D, через которую и проходит искомая прямая.

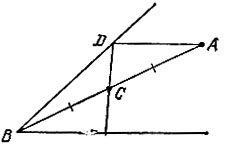
Рис. 166

19.75. Диаметром наименьшего круга, содержащего указанный треугольник, является наибольшая сторона этого тупоугольного треугольника, равная 4.

19.76. Крепче держится треугольный гвоздь, поскольку соприкасается с окружающей его древесиной по наибольшей поверхности: при равных площадях сечения периметр значения будет наибольшим у треугольника и наименьшим круга (отсюда, кстати, следует, что круглый гвоздь держится слабее любых других гвоздей).

19.77. Частей не могло быть 66, но могло быть 67, так при каждом измельчении листа число кусочков увеличивалось на 3, а вначале это число было равно 1.

19.78. На рис. 167 показано, как разрезать квадрат на 4, 6 или 8 квадратов. Деля любую из полученных частей на 4 квадрата, мы будем увеличивать их число на 3. Таким образом, из исходного квадрата можно получить разрезанием как 4 квадрата, так и любое их число, большее 5.

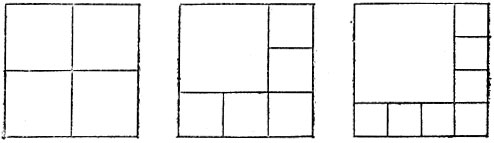
Рис. 167

19.79. Число разломов не зависит от порядка, в котором они производятся. Это число будет на единицу меньше, чем количество квадратных долек, составляющих плитку шоколада, поскольку после первого разлома образуются два куска шоколада, после второго-три, после третьего-четыре и т. д.

19.80. Достаточно двух цветов. Это доказывается индукцией по числу прямых линий, делящих страну на области.

19.81. Сложив лист пополам, разрежем его так, как показано на рис. 168.

Рис. 168

19.82. Разобьем имеющиеся треугольники на пары и сложим из них одинаковые параллелограммы, а затем замостим всю плоскость такими параллелограммами (рис. 169).

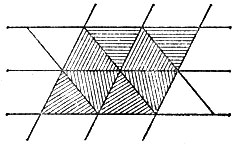
Рис. 169

19.83. Для паркета годятся любые одинаковые четырехугольники: сначала замостим всю плоскость параллелограммами, построенными на диагоналях данного четырехугольника как на сторонах, а затем в каждый параллелограмм поместим по данному четырехугольнику (на рис. 170 они заштрихованы), а остальные части плоскости автоматически окажутся такими же, но повернутыми четырехугольниками.

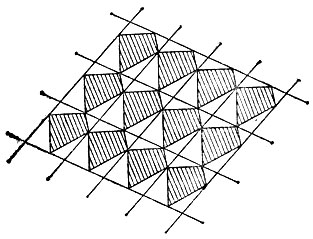
Рис. 170

19.84. Годится любая прямая, проходящая через точку пересечения диагоналей прямоугольника.

19.85. Достаточно провести разрез через центры симметрии прямоугольника и параллелограмма.

19.86. Достаточно, например, разрезать треугольник на три части, на которые его разбивают перпендикуляры к сторонам, опущенные из центра вписанной окружности (рис. 171).

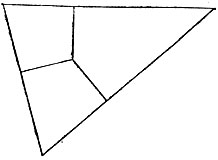
Рис. 171

19.87. Пусть требуется провести разрез через вершину А четырехугольника ABCD. Через середину О диагонали BD проведем прямую, параллельную другой диагонали АС, до пересечения со стороной ВС или CD в точке Е (рис. 172). Тогда прямая АЕ делит четырехугольник ABCD на равновеликие части.

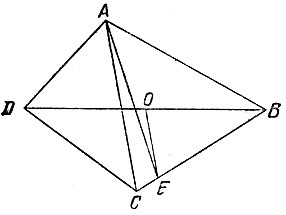
Рис. 172

19.88. Приставим один из меньших квадратов к другому и отрежем от них два исходных прямоугольных треугольника, переложив их так, как показано на рис. 173.

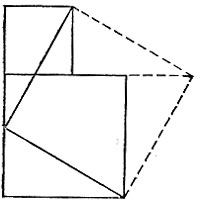
Рис. 173

19.89. Если мысленно разрезать данный ящик на два ящика размером 20*15*9 и 20*15*5, то в каждом из них одно измерение будет делиться на 10, другое на 5 и еще одно на 3. Поэтому оба ящика, а значит, и исходный можно заполнить коробками.

19.90. Можно разместить 68 кругов так, как изображено на рис. 174. При этом останется неиспользованной полоска шириной

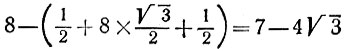
(последняя величина положительная, поскольку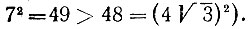

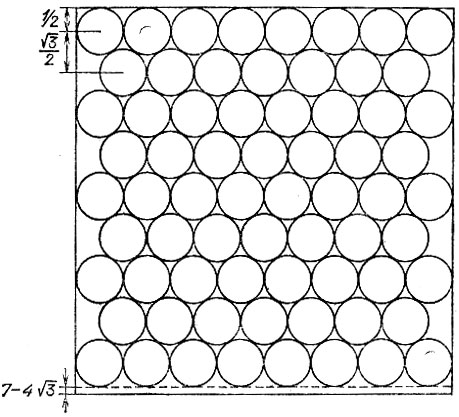
Рис. 174

19.91. Если бы это было возможно, то в круге радиуса 550 м можно было бы разместить без наложений 125 кружков радиуса 50 м каждый с центрами в скважинах. Но тогда общая площадь этих кружков, равная 125*2500*π м² была бы меньше площади объемлющего круга, равной 550*550π м², что не соответствует истине. Значит, указанное размещение скважин невозможно.

19.92. Если данная точка С не принадлежит окружности, то найдем точки D и Е пересечения прямых АС и ВС с окружностью, а затем точку F пересечения прямых АЕ и BD (рис. 175). Тогда прямая CF представляет собой искомый перпендикуляр.

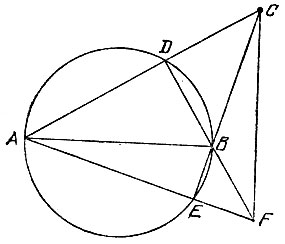
Рис. 175

Если же точка С лежит на окружности, то проведем какой-либо перпендикуляр к диаметру АВ, пересекающий окружность в точках К и L (рис. 176), а затем найдем точки М и N пересечения прямой CL с диаметром АВ и прямой КМ с окружностью соответственно. Тогда прямая CN будет также перпендикулярна диаметру.

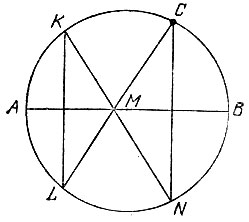
Рис. 176

19.93. Проведя на одинаковых расстояниях (равных ширине h линейки) от сторон данного угла параллельные прямые (рис. 177), мы получим ромб, диагональ которого делит угол пополам.

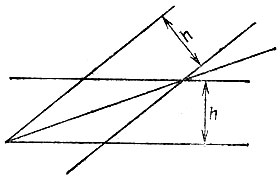
Рис. 177

19.94. Проведем по одинаковому количеству прямых, параллельных обеим сторонам угла, на расстояниях, кратных ширине h линейки. Соответствующие точки пересечения этих прямых лежат на биссектрисе угла (рис. 178).

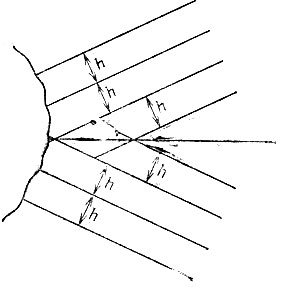
Рис. 178

19.95. Проведем прямую, параллельную данному отрезку АВ, и построим треугольник АСВ, стороны АС и ВС которого пересекают прямую в точках D и Е (рис. 179). Тогда, проведя через точку F пересечения прямых АЕ и BD прямую CG, мы разделим отрезок АВ пополам.

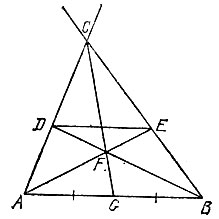
Рис. 179

19.96. Используя конструкцию, описанную в решении задачи 19.95, построим два равнобедренных треугольника A₁С₁B₁ и А₂С₂В₂ (рис. 180) и проведем их медианы, на пересечении которых как раз и будет лежать центр окружности.

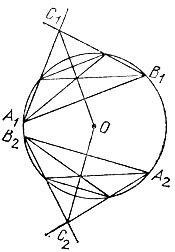
Рис. 180

19.97. Отложив на данной прямой две точки на расстоянии друг от друга, большем ширины h линейки, приложим двустороннюю линейку так, чтобы оба раза отмеченные точки примыкали к разным сторонам линейки (рис. 181). Проведя четыре соответствующие прямые, получим в пересечении ромб с одной диагональю, лежащей на данной прямой, и с другой диагональю, ей перпендикулярной.

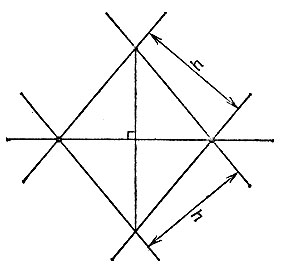
Рис. 181

19.98. Отложим на сторонах угла от его вершины по два отрезка длиной 1 см каждый (см. задачу 9.7 и рис. 10). Соединив четыре полученные точки попарно крест-накрест, мы получим точку биссектрисы (рис. 182).

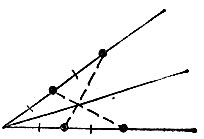
Рис. 182

19.99. Впишем в данную окружность два прямых угла, которые будут опираться на диаметры (рис. 183). Тогда точка пересечения этих диаметров укажет центр окружности.

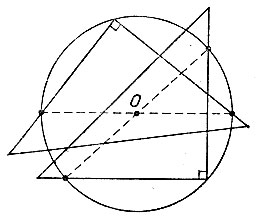
Рис. 183

19.100. Построим два прямоугольника с общей стороной, совпадающей с данным отрезком. Тогда, соединив друг с другом точки пересечения их диагоналей, мы найдем середину этого отрезка (рис. 184).

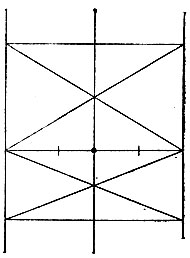
Рис. 184

19.101. Можно сильно приблизить друг к другу вершины исходного прямоугольника, перенеся каждую из них вдоль длинной стороны к ее середине на ширину шоколадки (рис. 185).

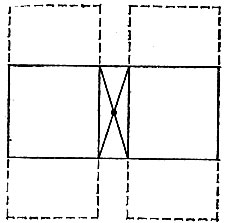
Рис. 185

19.102. Проведем какую-либо дугу с центром в данной точке А, чтобы получились две точки В и С пересечения с исходной дугой (рис. 186). Затем найдем точку D, отличную от точки А и равноудаленную от точек В к С. Прямая AD будет искомой.

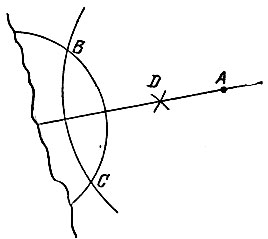
Рис. 186

19.103. Построим точку С на равном расстоянии от точек А и В и отложим на луче ВС точку В на том же расстоянии от точки С (рис. 187). Тогда угол BAD будет прямым.

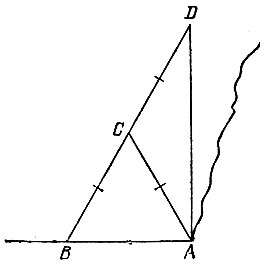
Рис. 187

19.104. Положим бумагу на цилиндрический предмет, например на трубу, и, установив одну ножку циркуля на полученной поверхности, проведем на ней циркулем "окружность" (рис. 188). Распрямив затем лист, получим на нем кривую овальной формы.

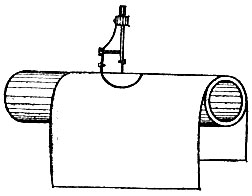
Рис. 188

19.105. Точки А, В, С, D (первые две точки считаем данными) на рис. 189 лежат на одной прямой, при этом все дуги одинакового радиуса АВ проводятся последовательно с центрами в В, А, Е, F, С, G.

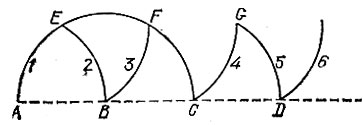
Рис. 189

19.106. По данным концам отрезка А В построим точку С так, как указано в решении задачи 19.105. Затем проведем дугу 2 с центром С и радиусом АС. Наконец, проведем дугу 3 с центром D (рис. 190) и радиусом AD, которая пересечет отрезок АВ в его середине М (если даже отрезок АВ, как таковой, не проведен, точку М можно построить, проведя дополнительно дугу 4 с центром Е).

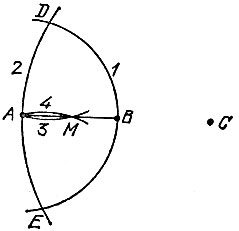
Рис. 190

19.107. Проведем окружность с центром О и радиусом 1 и, не меняя раствора циркуля, отложим на ней точки А, В, С, D (рис. 191). Тогда расстояние между точками А и С равно , а точка Е пересечения двух дуг с центрами А, D и радиусом удалена от точки О на расстояние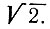

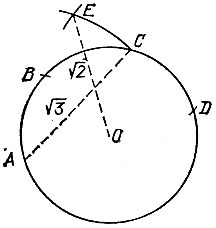
Рис. 191

19.108. Для нахождения центра О данной окружности достаточно провести дугу 1 с центром в некоторой точке А этой окружности (рис. 192), затем еще две дуги 2 и 3 того же радиуса с центрами В и С, далее дугу 4 с центром D и радиусом AD и, наконец, две дуги 5 и 6 с центрами Е и F и радиусом АЕ, которые как раз пересекутся в точке О.

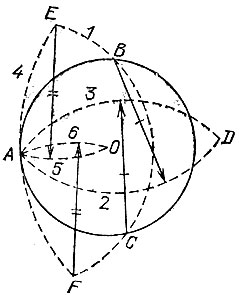
Рис. 192

19.109. Чтобы по данной точке А построить точку В, лежащую на одной прямой с точкой А и вершиной угла, достаточно выбрать точку С и провести последовательно прямые линии 1-7 так, как указано на рис. 193.

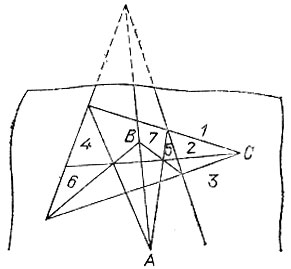
Рис. 193

19.110. Пусть надо соединить прямой линией точки А и В, Заметим, что короткой линейкой мы можем продолжать любую прямую по заданному ее участку. Пользуясь этим замечанием, проведем прямые 1, 2 через точку В так, чтобы они прошли близко от точки А. Затем из некоторой точки С выпустим достаточно густой пучок прямых: на рис. 194 это прямые 3-13. Далее проведем прямые 14-17 и найдем точку D, затем аналогично точки Е, F, G, H, которые все будут лежать на прямой АВ и позволят построить эту прямую короткой линейкой.

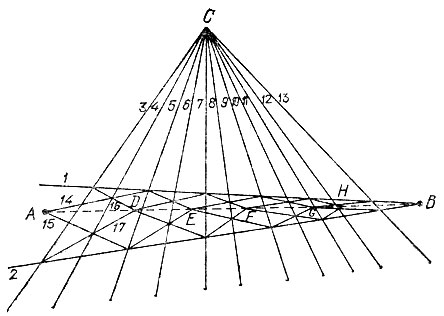
Рис. 194

19.111. Через некоторую точку данной прямой проведем две прямые 1, 2, а через некоторую точку А проведем четыре прямые 3-6 так, как показано на рис. 195. Выбрав на данной прямой удобную точку В, проведем последовательно прямые 7-12. Тогда точки пересечения прямых 9, 10 и прямых 11, 12 будут лежать на продолжении данной прямой за кляксу.

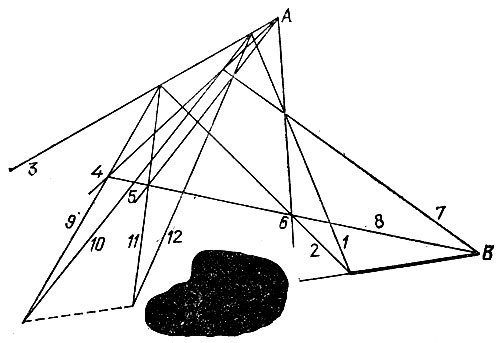
Рис. 195

© Издательство "Наука". Главная редакция физико-математической литературы, 1989

Научно-популярное издание

Сергеев Игорь Николаевич

Олеxник Слав Николаевич

Гашков Сергей Борисович

Примени математику

Заведующий редакцией А. П. Баева

Редактор М. М. Горячая

Художник П. И. Чернуский

Художественный редактор Г. М. Коровина

Технический редактор И. Ш. Аксельрод

Корректоры Н. Д. Дорохова, Н. Б. Румянцева

ИБ № 32682

Сдано в набор 26.01.89. Подписано к печати 25.07.89. Формат 84*108 ¹/₃₂. Бумага офс. № 2. Гарнитура литературная. Печать высокая. Усл. печ. л. 12,6. Усл. кр.-отт. 13,07. Уч.-изд. л. 12,65. Тираж 200 000 экз. Заказ №9-142. Цена 55 коп.

Ордена Трудового Красного Знамени издательство "Наука" Главная редакция физико-математической литературы

117071 Москва В-71, Ленинский проспект, 15

Ордена Октябрьской Революции и ордена Трудового Красного Знамени МПО "Первая Образцовая типография" Государственного комитета СССР по делам издательств, полиграфии и книжной торговли. 113054 Москва, Валовая, 28

Отпечатано на полиграфкомбинате ЦК ЛКСМ Украины "Молодь" ордена Трудового Красного Знамени издательско-полиграфического объединения ЦК ВЛКСМ "Молодая гвардия". 252119 Киев-119, ул. Пархоменко, 38-44.

MAKE USE OF MATHEMATICS by I. N. Sergeev, S. N. Olehnic, S. B. Gashkov.

A great number of problems are given in the book. They are all of practical character. Methods of fast counting are also considered as well as geometric constructions and measurements carried and with the help of a limited number of tools. The book also deals with methods of finding the most economic means for solving problems in various situations, also problems on mixing of substitunces, cutting up geometric figures, weighing, pouring and so on. All problems are supplied with solutions.

The aim of the book is to teach how to apply mathematical ideas and methods to finding a way out of various complicated situations that may arise.

The book is meant for schoolchildren, teachers and those who are interested in mathematics.

The authors are teachers of mathematics at the Mechanics and Mathematics Department of Moscow University.

They have already published a number of books on mathematics for schoolchildren and college and university students. Some of the books have been published abroad.