Решения

15.1. Если все я сторон вписанного я-угольника стягивают равные дуги окружности, то сами стороны равны между собой. Кроме того, в этом случае каждый из углов между соседними сторонами n-угольника является вписанным и опирается на дугу, составленную из n-2 упомянутых одинаковых дуг. Следовательно, все эти углы также равны между собой. Таким образом, задача построения вписанного правильного n-угольника сведена к делению окружности на я равных дур.

Если под рукой имеется транспортир, то с его помощью 360° можно начертить центральный угол, равный 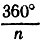. Отложив один такой угол от какого-нибудь радиуса OA₁, мы получим радиус ОА₂. Отложив от него еще один такой же угол, мы получим следующий радиус OA₃ и т. д. Точки A₁, A₂, ..., A_n будут делить окружность на n частей, а уж в какой степени эти части окажутся равными, будет зависеть от точности, с которой откладывались требуемые центральные углы.

При отсутствии транспортира можно применить следующий способ приближенного деления окружности на заданное число n равных частей с помощью циркуля. Выберем раствор циркуля на глаз таким, чтобы он примерно соответствовал расстоянию между соседними вершинами будущего n-угольника, и отложим от любой точки А₆ на окружности n растворов циркуля в определенном направлении, получив последовательно точки A₁, A₂, ..., A_n. Если точки A₀ и А_n практически совпадают, то раствор циркуля выбран нами уже достаточно точно. Если же эти точки сколь-нибудь заметно различаются, то дугу A₀A_n разделим на n примерно равных частей и отметим ту точку деления A₀, которая расположена ближе всего к точке A₀ (рис. 49). Подправим раствор циркуля так, чтобы он соответствовал расстоянию между точками A'₀ и A'₁, и повторим все сначала, отложив n растворов циркуля от точки A'₀ и получив точки A'₁, A'₂, ..., A'_n. Сравнив точки A'₀ и A'_n, мы опять выясним, достаточно ли точным оказался раствор циркуля. Если еще нет, то подправим его еще раз и т. д. до тех пор, пока нужная точность не будет достигнута.

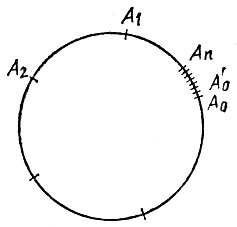
Рис. 49

15.2. Пусть A₁, A₂, ..., A_km - последовательные вершины исходного многоугольника. Тогда многоугольник с вершинами A₁, A₂, ..., A_km будет правильным, поскольку эти вершины лежат на одной окружности (описанной около исходного многоугольника) и делят ее на равные дуги.

15.3. Проведем к каждой стороне данного многоугольника свой серединный перпендикуляр до его пересечения о дугой окружности, стягиваемой этой стороной. Так как полученные точки пересечения разделят каждую из дуг на две равные части, то эти точки вместе с вершинами исходного многоугольника образуют вершины требуемого многоугольника.

15.4. Пусть АВ - заданный отрезок. Проведем две дуги окружностей с центрами в точках A и B и радиусом AВ до пересечения их в точке С. Соединив точки A и B с точкой С, получим требуемый правильный треугольник ABC.

15.5. Возьмем на данной окружности с центром О произвольную точку A и раствором циркуля, равным ОА, отложим на окружности последовательно еще пять точек В, C, D, Е и F. Точки A, В, С, D, Е и F являются вершинами правильного шестиугольника. В самом деле, соединив эти точки последовательно друг с другом и с точкой О, мы получим пять равносторонних треугольников (рис. 50). Так как каждый из углов АОВ, ВОС, COD, DOE, EOF равен по 60°, то угол AOF также равен 60°, а, значит, окружность разделена на шесть равных дуг.

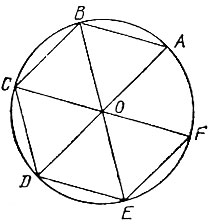
Рис. 50

15.6. Раствором циркуля, равным длине данного отрезка, проведем окружность. Вписав в эту окружность шестиугольник способом, предложенным в решении задачи 15.5, мы получим правильный шестиугольник с заданной стороной.

15.7. Разделим данную окружность на шесть равных частей (см. задачу 15.5) и точки деления через одну последовательно соединим хордами. Получим правильный треугольник (см. задачу 15.2).

15.8. Из концов данного отрезка АВ восставим перпендикуляры AM и BN по одну сторону от отрезка АВ (рис. 51) и отложим на них соответственно отрезки AD и ВС, равные отрезку АВ, Соединив точки С и D, получим квадрат ADCB. В самом деле, четырехугольник ADCB является параллелограммом (ибо его стороны AD и ВС равны и параллельны), ромбом (ибо АВ = ВС) и прямоугольником (ибо ∠ ABC = 90°), а значит, квадратом.

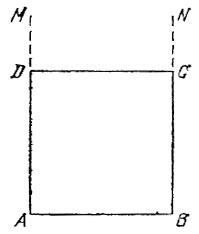
Рис. 51

15.9. Через центр окружности проведем два взаимно перпендикулярных диаметра АС и BD и их концы последовательно соединим хордами. Получим вписанный квадрат ABCD. Действительно, дуги АВ, ВС, CD и AD равны между собой, поскольку на них опираются равные центральные углы в 90° каждый.

15.10. Впишем в данную окружность квадрат (см. задачу 15.9) и удвоим число его сторон (см. задачу 15.3).

15.11. Удвоив число сторон правильного вписанного в данную окружность шестиугольника, мы получим правильный двенадцатиугольник, вписанный в ту же окружность (см. задачи 15.5 и 15.3).

15.12. Удвоив число сторон правильного вписанного в данную окружность восьмиугольника, мы получим правильный шестнадцатиугольник, вписанный в ту же окружность (см. задачи 15.10 и 15.3).

15.13. Из середины С данного отрезка АВ (рис. 52) восставим перпендикуляр и отложим на нем отрезок CD, равный ¹/₂ АВ. Затем на его продолжении отложим отрезок DO, равный AD. Тогда отрезок АО является радиусом окружности, описанной около правильного восьмиугольника со стороной АВ.

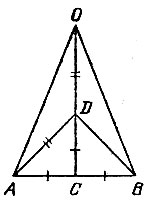
Рис. 52

В самом деле, найдем величину угла АОС. Так как АС = CD, то треугольник ACD равнобедренный, и так как он прямоугольный, то угол ADC равен 45°. Поскольку AD = DO, то треугольник ADO равнобедренный и угол AOD равен 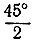и, следовательно, угол АОВ равен 45°, т. е. дуга АВ есть ¹/₈ часть окружности.

Теперь на окружности радиуса АО от любой точки последовательно отложим семь дуг, каждая из которых равна дуге АВ. Получим вершины правильного восьмиугольника.

15.14. Построим равносторонний треугольник АСВ со стороной, равной данному отрезку АВ. Через точку С проведем прямую, перпендикулярную отрезку АВ. Отложим на этой прямой отрезок СО, равный АВ (рис. 53). Тогда отрезок АО является радиусом окружности, описанной около правильного двенадцатиугольника со стороной АВ. Для подтверждения этого достаточно доказать, что угол АОВ равен 30°. Точка С равноудалена от точек А, В и О, т. е. является центром окружности, описанной около треугольника АОВ. Поэтому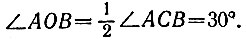

Рис. 53

Теперь на окружности радиуса AО от любой точки последовательно отложим 11 дуг, каждая из которых равна дуге АВ. Получим вершины правильного двенадцатиугольника.

15.15. Из середины С отрезка АВ восставим перпендикуляр (рис. 54) и на нем отложим отрезок CD9 равный ¹/₂ АВ, затем отрезок DE, равный AD, и отрезок ВО, равный АЕ. Тогда отрезок АО является радиусом окружности, описанной около правильного шестнадцатиугольника со стороной АВ.

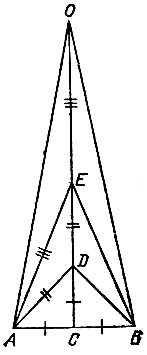
Рис. 54

Так же как и в задаче 15.13, находим, что

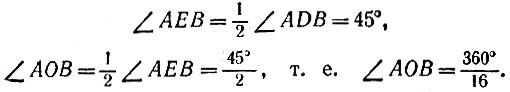
Построение правильного шестнадцатиугольника выполняется аналогично построению в предыдущих задачах.

Теперь на окружности радиуса АО от любой точки последовательно отложим 15 дуг, каждая из которых равна дуге АВ. Получим вершины правильного шестнадцатиугольника.

15.16. Пусть заданный отрезок АВ имеет длину а. Найдем длину х большей части "золотого сечения" отрезка АВ. Из пропорции

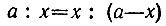
получаем

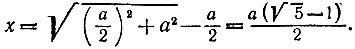
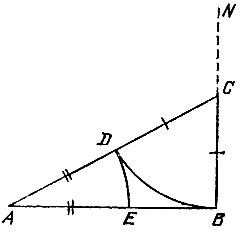
Рис. 55

Следовательно, задача сводится к построению отрезка указанной длины х по отрезку длины а. Число 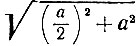равно длине гипотенузы прямоугольного треугольника с катетами а и ^а/₂, который можно построить с помощью циркуля и линейки. Для получения отрезка длины 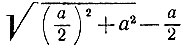достаточно из гипотенузы построенного треугольника вычесть отрезок длины ^а/₂. Следовательно, построение "золотого сечения" отрезка АВ можно произвести следующим образом (рис. 55):

* из точки В восставим перпендикуляр BN к отрезку АВ, на нем отложим отрезок ВС длины ¹/₂ АВ;

* соединим точки А и С и отложим на отрезке АС отрезок DC длины ВС;

* отложим на отрезке АВ отрезок АЕ длины AD, тогда точка Е делит отрезок АВ в "золотом сечении".

15.17. Пусть АВ - сторона правильного вписанного в окружность десятиугольника. Тогда ∠ AОВ = 36°, а каждый из углов ОАВ и АВО равен 72° (рис. 56). Проведем биссектрису АС угла A треугольника АОВ. Так как ∠ AСВ = 72°, то из равнобедренных треугольников ABC и АСО получим AB = AС = ОС.

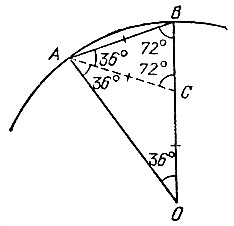
Рис. 56

По свойству биссектрисы треугольника имеем ОС:ВС = АO:АВ. Поскольку АО = ОВ, АВ = ОС, то ОС:ВС = ОВ:ОС, т. е. ОС² = ВС*ОВ, а это и означает, что радиус ОВ разделен точкой С в "золотом сечении", причем ОС - большая часть радиуса (ибо ∠ ACB> ∠BAC, откуда ОС = АВ>ВС).

Таким образом, разделив радиус ОВ данной окружности в "золотом сечении" (см. задачу 15.16) и взяв большую его часть ОС, мы найдем длину стороны А В правильного вписанного в эту окружность десятиугольника. Теперь от любой точки данной окружности последовательно отложим девять хорд, каждая из которых равна АВ. Один из конкретных способов построения стороны ОС = АВ требуемого десятиугольника приведен на рис. 57.

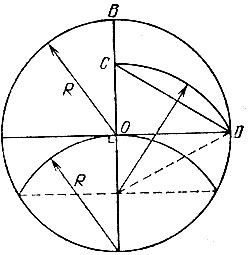
Рис. 57

15.18. Разделим данную окружность на 10 равных частей (см. задачу 15.7). Тогда точки деления, взятые через одну, являются вершинами правильного пятиугольника (см. задачу 15.2). Впрочем, на рис. 57, где построен отрезок ОС, равный стороне правильного вписанного десятиугольника, имеется и отрезок CD, равный стороне требуемого пятиугольника.

15.19. Нарисуем некоторую окружность, разделим ее на 5 равных частей (см. задачу 15.18) и соединим точки деления через одну хордами друг с другом, как указано на рис. 58.

Рис. 58

15.20. Поскольку ¹/₆ - ¹/₁₀ = ¹/₁₅, то, отняв от дуги, равной ¹/₆ окружности, дугу, равную ¹/₁₀ окружности, мы получим остаток, равный ¹/₁₅ окружности. Это наблюдение позволяет вписать в окружность правильный пятнадцатиугольник (способы деления окружности на 6 и 10 частей описаны в задачах 15.5 и 15.17).

15.21. Из конца А и середины С заданного отрезка АВ восставим перпендикуляры АN и СМ и проведем окружность с центром А и радиусом АВ (рис. 59). Отложим на перпендикуляре AN отрезок AD длины АС и проведем отрезок BD. Отложим на отрезке BD отрезок DE длины AD и проведем окружность с центром В и радиусом BE до пересечения с первой окружностью в точке F. На прямой AF построим точку G на расстоянии АВ от точки В, Тогда центр О окружности, описанной около правильного пятиугольника со стороной АВ, лежит на пересечении прямой СМ с серединным перпендикуляром к отрезку BG. Действительно, окружность, описанная около треугольника ABG, является описанной и около требуемого пятиугольника, так как вписанный угол BAG равен центральному углу BAF, опирающемуся на сторону FB десятиугольника, вписанного в первую окружность (см. задачу 15.17), и, следовательно, равному 36°. Поэтому углы BOG и AOB равны 72° каждый. Остальные две вершины пятиугольника лежат на пересечениях описанной окружности с перпендикуляром СМ и с первой окружностью соответственно.

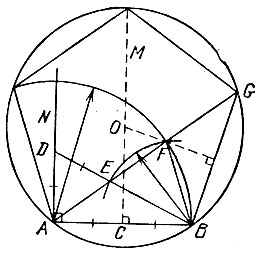
Рис. 59

15.22. Построенный семиугольник не является правильным. В самом деле, пусть О - центр окружности, точка D - середина стороны АВ правильного треугольника, а точка Е - первая из засечек, сделанных на окружности радиусом 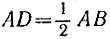(рис. 60). Найдем величину α угла АОЕ.

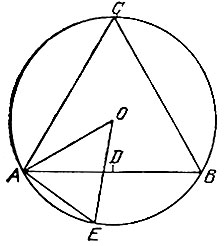
Рис. 60

Пусть R - радиус окружности, тогда 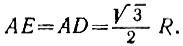Из равнобедренного треугольника АОЕ имеем

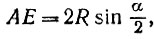
откуда

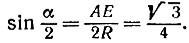
По таблицам синусов находим, что

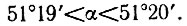
Центральный угол β опирающегося на сторону правильного семиугольника равен ^360°/₇, т. е.

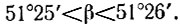
Следовательно, построенный семиугольник не является правильным. Однако из приведенных неравенств следует,

что

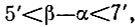
а значит, в результате шести откладываний дуги АЕ на окружности погрешность построений хотя и будет накапливаться, но не превзойдет 6(β - α)<42'<1°. Таким образом, описанный способ позволяет строить "практически правильный" семиугольник.

15.23. Пусть D-точка пересечения отрезков ВС и OA₁, Е - середина отрезка ОА₁, a CF - перпендикуляр к прямой A₁E (рис. 61). Тогда если OA₁ = R, то 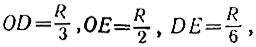а из прямоугольных треугольников А₂ОЕ и A₂CF имеем

откуда получаем

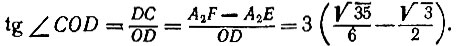
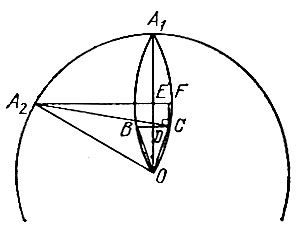
Рис. 61

По таблицам тангенсов находим

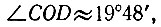
поэтому центральный угол BОС, который должен составлять у правильного девятиугольника 40°, в нашем случае отличается от нужного значения не более чем на 25'. При этом погрешность у остальных углов также не превосходит 25': два других "лепестка" дают такие же углы, а углы между "лепестками" просто делятся пополам, отчего погрешность лишь уменьшается в два раза. Таким образом, полученный девятиугольник является "практически правильным".

15.24. Заметим, что при n = 3, 4, 6 предложенный метод дает правильные n-угольники. Пусть О - центр данной окружности, R - ее радиус, EF - перпендикуляр к диаметру АВ (рис. 62). Тогда при n>4 справедливы равенства

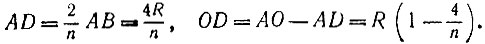
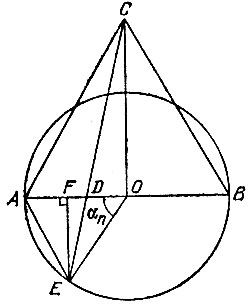
Рис. 62

Для угла 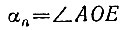имеем

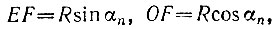
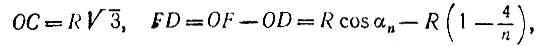
а из подобия треугольников DOC и DFE получаем

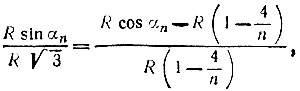
откуда после преобразований находим

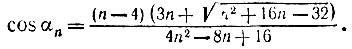
Подставляя в эту формулу значения n = 5, 7, 8, 9, 10, получаем следующие углы:

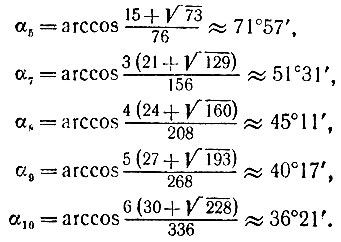
Сравнение с истинными значениями центральных углов, каковыми являются соответственно углы 72°, 51³/₇° ≈51°26', 45°, 40°, 36°, показывает, что при n≤7 метод дает исключительно высокую точность, а с ростом n погрешность растет. Однако преимущество этого метода состоит в том, что его можно единообразно использовать при различных значениях n.