§ 16. Построения на клетчатой бумаге

С бумагой в клетку каждый из вас имеет дело практически с первых дней изучения математики, а может быть, и раньше. Однако вы вряд ли представляете себе, насколько мощным инструментом для геометрических построений является наличие на бумаге квадратной сетки.

Условимся, пользуясь вольностью речи, разделять линии сетки на два вида: горизонтальные и вертикальные. Горизонтальными будем считать все параллельные линии сетки, имеющие какое-то фиксированное направление, а вертикальными - все остальные параллельные линии сетки, перпендикулярные горизонтальным. Точки пересечения линий сетки будем называть узлами, а расстояние между соседними узлами на одной линии - шагом сетки, причем по определению длину шага примем за единицу.

Важную роль при построениях на клетчатой бумаге играет возможность расположить фигуру так, чтобы все ее вершины или как можно большее их количество оказались в узлах сетки. В таких случаях построение некоторых точек фигуры иногда можно выполнить без каких-либо чертежных инструментов, а лишь о помощью подсчета числа шагов вдоль линий сетки. Заметим, что любой отрезок с концами в узлах сетки задается двумя своими проекциями - горизонтальной и вертикальной (т. е. его проекциями на некоторые горизонтальную и вертикальную линии сетки соответственно).

При решении задач настоящего параграфа стоит задумываться о том, чтобы предложенные вами способы построения использовали минимум технических средств. Если уж вам приходится применять, скажем, линейку, то только для проведения прямых линий между двумя заданными точками, но никак не для измерения расстояний между этими точками. Ну и, конечно, никому еще не повредило умение делать рисунки на бумаге от руки, даже рисовать окружности - ив этом деле, как мы увидим ниже, также помогает знание математики.

16.1. Середина отрезка На клетчатой бумаге нарисован отрезок, концы которого находятся в узлах сетки. Вам нужно найти его середину. Укажите, при каких положениях отрезка это можно сделать, не проводя дополнительных линий, а используя лишь точки пересечения отрезка с линиями сетки?

Как с помощью линейки найти середину отрезка при других его положениях?

16.2. Симметрия относительно точки Как проще всего найти точку, симметричную данному узлу сетки относительно другого данного узла сетки? Будет ли эта точка также узлом сетки?

16.3. На n частей Как разделить на заданное число n равных частей данный отрезок с концами в узлах сетки, пользуясь разве только линейкой?

16.4. Медианы треугольника В данном треугольнике с вершинами в узлах сетки проведите медианы, пользуясь одной лишь линейкой.

Обязательно ли точка пересечения медиан является узлом сетки?

16.5. Параллельный перенос Точки А, В и С находятся в узлах сетки. Не проводя никаких линий, параллельно перенесите точку С на вектор .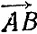

Будет ли полученная в результате точка узлом сетки?

16.6. Середина третьей стороны Докажите, что если какая-то вершина треугольника и середины двух прилежащих к ней сторон находятся в узлах сетки, то и середина третьей стороны также совпадает с одним из узлов сетки.

16.7. Параллельные прямые Через заданный узел сетки с помощью одной линейки проведите прямую, параллельную данной прямой, проходящей через два данных узла сетки. Отразите проведенную прямую симметрично относительно той же данной прямой.

16.8. Поворот на 90° Не проводя никаких линий, найдите точку, которая получится, если повернуть данный узел сетки вокруг другого данного узла сетки на угол 90°.

16.9. Вершины квадрата Докажите, что если две заданные соседние вершины квадрата находятся в узлах сетки, то и остальные две его вершины также должны находиться в узлах сетки.

Найдите эти вершины, не проводя никаких линий.

16.10. Перпендикуляр к прямой С помощью одной линейки через заданный узел сетки проведите прямую, перпендикулярную данному отрезку с концами в узлах сетки.

16.11. Симметрия относительно прямой Пользуясь одной лишь линейкой, отразите симметрично заданный узел сетки относительно данной прямой, проходящей через два данных узла сетки. Будет ли полученная в результате точка узлом сетки?

16.12. Рациональный тангенс Докажите, что проходящая через некоторый узел сетки прямая содержит еще хотя бы один узел тогда и только тогда, когда она образует с какой-нибудь линией сетки угол, тангенс которого является рациональным числом.

16.13. Без транспортира Найдите величину угла ABC, изображенного на рис. 63. Пользуясь полученным значением, сообразите в уме, чему равна сумма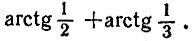

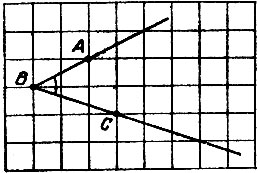
Рис. 63

16.14. С помощью клетчатой бумаги На середине стороны АВ квадрата ABCD взята точка Е, а на диагонали АС - точка F, делящая диагональ в отношении AF:FC = 3:1 (рис. 64). Найдите угол DFE и отношение DF:FE.

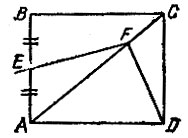
Рис. 64

16.15. Геометрия помогает тригонометрии Расположив на клетчатой бумаге угол DFE, описанный в задаче 16.14 и изображенный на рис. 64, подберите на луче FE несколько узлов сетки так, чтобы продемонстрировать равенства

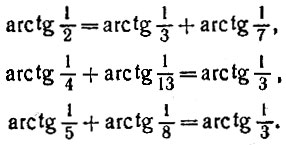
16.16. Тангенсы углов треугольника Докажите, что если вершины треугольника лежат в узлах сетки, то тангенс любого непрямого угла этого треугольника является рациональным числом.

16.17. Другие повороты Прямая проходит через два заданных узла сетки. Предложите способ, как повернуть указанную прямую вокруг одного из этих узлов на угол, тангенс которого равен данному рациональному числу.

16.18. Правильный треугольник Докажите, что все вершины равностороннего треугольника не могут одновременно лежать в узлах сетки.

16.19. Правильный шестиугольник Могут ли все вершины правильного шестиугольника одновременно лежать в узлах сетки?

16.20. Одной окружностью Вы хотите разметить циркулем на клетчатой бумаге вершины правильного шестиугольника. Пользуясь циркулем, вы, конечно, всегда сможете это сделать на любой бумаге (см. задачу 15.5). Нельзя ли, однако, воспользоваться имеющейся сеткой с тем, чтобы после проведения специально подобранной вами окружности линии сетки сами указали вам на окружности вершины правильного шестиугольника?

16.21. Квадрат по трем линиям сетки На клетчатой бумаге требуется разметить вершины квадрата таким образом, чтобы три из них лежали соответственно на трех заданных параллельных линиях сетки. Как это сделать, не проводя никаких дополнительных линий?

Можно ли, кроме того, обеспечить попадание также и четвертой вершины квадрата на какую-нибудь из трех указанных линий?

16.22. Правильный многоугольник При каких значениях n все вершины правильного n-угольника могут одновременно лежать в узлах сетки?

16.23. С горизонтальной гипотенузой Если вам приходилось рисовать на клетчатой бумаге прямоугольные треугольники, то, наверняка, порядком наскучило располагать их катеты по линиям сетки. Можно ли построить такой прямоугольный треугольник со всеми вершинами в узлах сетки, чтобы на линии сетки оказалась его гипотенуза?

Равнобедренный прямоугольный треугольник так расположить довольно несложно. Укажите способ построения всех таких треугольников.

16.24. Окружность от руки Для проведения без циркуля какой-нибудь окружности на клетчатой бумаге, можно воспользоваться тем, что окружность с центром в узле сетки и радиусом 5 проходит через 12 узлов, изображенных на рис. 65. Докажите этот факт.

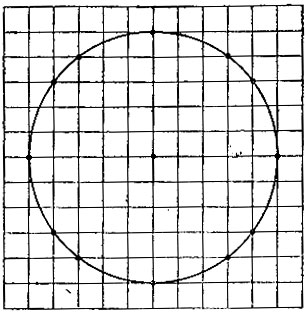
Рис. 65

Существует ли окружность с центром в узле сетки и целым радиусом, меньшим 5, также содержащая более 4 узлов?

16.25. Окружность с 20 узлами Какого наименьшего целого радиуса должна быть окружность с центром в узле сетки, содержащая более 12 узлов? Нарисуйте хотя бы четверть этой окружности.