§ 19. Маленькие хитрости

Книга подходит к концу. И если до сих пор к каждой задаче давалось достаточно подробное решение, то в настоящем параграфе вам представляется возможность решать задачи в большей степени самостоятельно.

Некоторые из предложенных ниже задач, возможно, покажутся вам слишком простыми, но и в таких случаях советуем не торопиться с ответом - можно попасть впросак. Приведенные решения в большинстве случаев очень кратки, они скорее напоминают указания к решениям. Вдумчивому читателю было бы полезно попробовать доказать самостоятельно сформулированные нами утверждения.

Большинство ситуаций, описанных в настоящем параграфе, встречаются в повседневной жизни и являются естественными. Однако для своего разрешения они порой требуют некоторой изобретательности и смекалки - этим и объясняется название параграфа.

19.1. Экономный счет У продавца в киоске конверты сложены в пачки по 100 штук. Как ему быстрее отсчитать 75 конвертов?

19.2. Стопка бумаги Как можно быстро определить примерное количество листов бумаги, содержащихся в данной большой стопке?

19.3. Множественная регистрация Вам нужно обработать огромную стопку анкет, каждая из которых содержит по несколько пунктов. Как нужно организовать одновременный подсчет тех или иных анкетных данных, чтобы, просмотрев всю стопку только один раз, можно было выдать исчерпывающую статистику по интересующим вас вопросам?

19.4. Гвозди в ящике Как приблизительно сосчитать число гвоздей в ящике?

19.5. День отъезда - день приезда Вы уехали в командировку 24 марта, а вернулись 31 марта. Сколько дней вы были в командировке?

19.6. Перекладывание конфет В двух пакетах лежат конфеты, причем в одном пакете на 10 конфет больше, чем в другом. Сколько конфет нужно переложить из одного пакета в другой, чтобы в них конфет стало поровну?

19.7. Заготовка дров Из трехметровых и четырехметровых бревен одинаковой толщины нужно заготовить машину дров, распилив бревна на куски длиной по одному метру. Какие бревна выгоднее пилить?

19.8. Пешком по ступеням Во сколько раз путь по лестнице на 16-й этаж дома длиннее пути на 4-й этаж?

19.9. Как разыскать нужную квартиру В одном из подъездов шестнадцатиэтажного дома на первом этаже находятся квартиры с номерами 65, 66, 67 и 68. В каком подъезде и на каком этаже находится квартира с номером 165?

19.10. Пирожок без бульона Находясь в столовой, вы прочитали в меню, что порция бульона с пирожком стоит 31 копейку, а половина порции бульона с пирожком стоит 23 копейки. Сколько стоит пирожок?

19.11. Сдавая посуду В буфете продается лимонад в бутылках стоимостью 30 копеек. Пустую бутылку можно вернуть, получив за нее 20 копеек. Какое наибольшее количество лимонада можно выпить, имея при себе 1 рубль?

19.12. В единую цепь Четыре обрывка цепи, содержащих по 2 звена каждый, нужно соединить в одну цепь. Можно ли это сделать, расклепав, а затем снова заклепав меньше, чем три звена?

19.13. Общий сейф Три инженера имеют общий сейф. Как запереть этот сейф, чтобы' открывать его можно было только при одновременном присутствии или при согласии всех трех инженеров?

19.14. Общая лодка Три рыбака имеют общую лодку, и у каждого из них есть свой замок и ключ к нему. Как прицепить лодку к берегу, чтобы любой из рыбаков мог ее отцепить с помощью одного только своего ключа.

19.15. Подбор ключей Вы рассыпали связку из 10 ключей от 10 дверей. Каждый ключ подходит только к одной двери. Как за наименьшее число попыток восстановить соответствие между ключами и дверями?

19.16. Пара носков В ящике комода лежат в беспорядке 20 носков: 10 коричневых и 10 черных. Какое наименьшее количество носков достаточно извлечь не глядя из ящика, чтобы среди них наверняка можно было выбрать пару одинаковых носков?

19.17. Пара перчаток В ящике комода лежат в беспорядке 20 перчаток: 5 пар коричневых и 5 пар черных. Какое наименьшее количество перчаток достаточно извлечь не глядя из ящика, чтобы среди них наверняка можно было выбрать пару одноцветных перчаток?

19.18. Трюк с перчатками Лаборанту-химику предстоит работать поочередно с тремя реактивами, вредными для кожи рук. Может ли он обойтись только двумя парами перчаток, если известно, что при работе с любым из этих реактивов на внешней поверхности перчаток непременно остаются частицы реактива, контакт которого с другими реактивами недопустим?

19.19. Угольник в кармане Из куска обыкновенной веревки можно устроить прямоугольный треугольник без использования линейки, транспортира и т. д. Как это сделать?

19.20. Скрепить узлом При обвязывании коробки веревкой часто приходится пересекать ранее сделанные витки. Придумайте способ, как скреплять пересекающиеся веревки узлом, не разрезая самих веревок.

19.21. Одним росчерком Вам нужно прострочить на одежде одну из эмблем, изображенных на рис. 136. Можно ли это сделать, не разрывая нитку в процессе шитья и не проходя ни по одной линии эмблемы дважды?

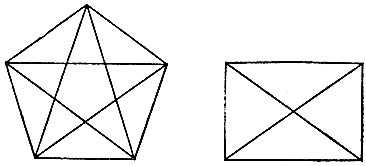
Рис. 136

19.22. Каркас куба Можно ли из целого куска проволоки длиной менее 1,5 м изготовить каркас куба с ребром 1 дм?

19.23. Экономное разрезание Разделите 5 яблок на 6 человек так, чтобы ни одно яблоко не пришлось разрезать на 6 частей.

19.24. На троих и четверых одновременно Вы купили торт для гостей, но не знаете точно, сколько всего будет человек - трое или четверо. Какое наименьшее число разрезов вы должны заранее сделать, чтобы в любом случае без дополнительных разрезов все могли получить торта поровну?

19.25. На восьмерых Какой торт можно разделить на восемь равных частей тремя прямыми разрезами?

19.26. Отмерить без измерений Как от куска материи длиной 8 м отрезать кусок длиной 5 м, не имея под рукой измерительных инструментов?

19.27. Усадка материи Во время стирки материя садится на ¹/₁₆ по длине и на ¹/₁₈ по ширине. Сколько метров материи шириной 0,9 м надо купить, чтобы после стирки иметь 51 м²?

19.28. Велик ли оставшийся кусок? После стирки кусок мыла уменьшился на ¹/₆ часть как по ширине, так и по высоте. На сколько таких же стирок хватит оставшегося куска мыла?

19.29. Статистическое исследование В одном городе Канады 70% жителей знают французский язык и 80% - английский язык. Сколько процентов жителей этого города знают оба языка?

19.30. Эффект снижения цены Пусть цены на какие-то товары снижены на 20%. На сколько процентов больше можно купить этих товаров по сниженной цене на отведенную для них сумму?

19.31. Денежный перевод За пересылку денег по почте с отправителя взимают 2% переводимой суммы, Какую наибольшую сумму денег можно перевести, имея на руках ровно 100 рублей?

19.32. Размеры и цены На рынке продаются два арбуза разных размеров: один арбуз в обхвате на четверть больше другого, зато в полтора раза дороже. Какой арбуз выгоднее купить?

19.33. Покупка мандаринов Какие мандарины - крупные или мелкие - выгоднее покупать, если толщина кожуры у них одинакова?

19.34. Хозяйке на заметку Какую картошку выгоднее чистить: крупную или мелкую?

19.35. Кажущаяся половина Из фужера конической формы, наполненного соком (рис. 137), отпили такую часть содержимого, что его высота уменьшилась вдвое. Какая часть была отпита?

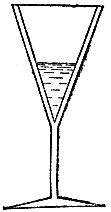
Рис. 137

19.36. Две кружки Одна кружка вдвое ниже другой, зато в полтора раза шире. Какая из двух кружек вместительнее?

19.37. Ровно полкружки Кружка цилиндрической формы наполнена доверху молоком. Можно ли отлить ровно половину содержащегося в ней молока, не пользуясь измерительными приборами?

19.38. Часть кюветы Вы хотите научиться заполнять водой для приготовления раствора какую-либо фиксированную часть кюветы (ванночки), имеющей форму прямоугольного параллелепипеда. Какие порции воды вы можете наливать, не пользуясь измерительными приборами и не делая отметок на стенках кюветы?

19.39. Объем бутылки Как, пользуясь одной лишь линейкой с делениями, определить полную вместимость круглой бутылки, частично заполненной жидкостью?

19.40. Объем любой фигуры Нужно вычислить объем небольшого предмета неправильной формы (камня, слитка и т. п.). Как это сделать?

19.41. Толщина слоя краски Вы покрасили пол в своей квартире. Можно ли приблизительно определить толщину получившегося при этом слоя краски?

19.42. Переливая воду Имеются пятилитровая банка и четырехлитровая каст-ля. Для приготовления супа надо налить в кастрюлю 3 л воды из-под крана. Как это сделать?

19.43. Разделить пополам В ведре содержится 10 литров молока. Требуется с помощью пустой трехлитровой банки и пустого семилитрового бидона распределить молоко так, чтобы в ведре и бидоне его оказалось по 5 литров. Как это сделать наименьшим числом переливаний?

19.44. Одной гирей Нужно отвесить на чашечных весах 13 кг сахарного песку при наличии всего лишь одной килограммовой гири. Конечно, 13 взвешиваний для этого вполне достаточно. Нельзя ли, однако, обойтись существенно меньшим их числом?

19.45. Оптимальный набор гирь Каким наименьшим числом и каких именно гирь нужно запастись, чтобы сих помощью можно было отвесить любое целое число килограммов от 1 до 13 при условии, что гири разрешается класть

а) только на одну чашку весов;

б) на обе чашки весов?

19.46. На грубых весах Положите копейку на обычные весы со стрелкой (которые имеются практически в любом магазине) и попробуйте таким образом определить вес монеты. Вряд ли вам удастся это сделать, поскольку стрелка весов отклонится слишком незначительно. Как же все-таки взвесить копейку на таких весах?

19.47. Расставить по порядку Вы хотите расположить несколько данных предметов в порядке возрастания их весов. Для этого вы можете выбирать любые два предмета и сравнивать их друг с другом, кладя их на разные чашки весов (без стрелок и без гирь). Конечно, можно было бы сравнить каждый предмет с каждым, но при этом, по всей видимости, была бы проделана лишняя работа.

Какое наименьшее число сравнений является заведомо достаточным, если количество предметов равно: а) 3; б) 4; в) 5?

19.48. Формула для максимума Предположим, что калькулятор имеет помимо четырех арифметических операций также и операцию взятия абсолютной величины числа. Придумайте формулу, по которой на этом калькуляторе можно найти наибольшее из двух произвольных чисел.

19.49. Перевозка ящиков Вес нескольких ящиков с грузом в общей сложности составляет 10 т, причем каждый ящик весит не более 1 т. За какое наименьшее количество поездок трехтонная машина заведомо сможет перевезти весь этот груз?

19.50. На неправильных весах Вы хотите отвесить 2 кг сахару на неравноплечих чашечных весах с помощью одной килограммовой гири. Подумайте над вопросом: больше или меньше 2 кг сахару вы получите, если отвесите 1 кг на одной чашке весов и еще 1 кг на другой? Можно ли на таких весах отвесить ровно 2 кг?

19.51. Простейшие весы Знаете ли вы, что весы можно изготовить из самой обыкновенной линейки с делениями для взвешивания, на которой нужна всего одна гиря? Если не знаете, то придумайте, как это сделать.

19.52. Сверка часов Вы хотите установить более точное время на стенных часах в вашем доме. Ближайшие часы находятся в нескольких минутах ходьбы и показывают правильное время, однако отнести туда стенные часы вы не можете.

Как поступить?

19.53. Распределение работы Одна машинистка печатает страницу текста в среднем за 6 минут, а другая - за 10 минут. В каком отношении нужно распределить между ними работу по печатанию рукописи, чтобы эта работа была завершена в кратчайшее время? i

19.54. Без замены шин Зная, через сколько километров пути стираются шины на передних и задних колесах легкового автомобиля, придумайте способ, как максимально удлинить его пробег, не заменяя шин ни на одном из четырех колес автомобиля.

19.55. Суммарный эффект Внедрение одного изобретения сокращает производственные затраты на 50%, второго - на 40%, а третьего - на 10%, На сколько процентов позволит сократить производственные затраты внедрение всех трех изобретений сразу?

19.56. Постоянное пастбище На лугу растет трава. На этот луг пустили 30 коров, которые за 4 дня съели всю траву. Когда на лугу снова выросла трава, на него пустили 25 коров, которые съели всю траву за 6 дней. Какое наибольшее количество коров может пастись на лугу все время (пока вообще растет трава)?

19.57. Обойдя вокруг Парашютист приземлился ночью около стены, окружающей некоторый участок земли в форме многоугольника. Пройдя вдоль всей стены и замерив какие-то углы, парашютист определил, где он находится: внутри участка или снаружи.

Как он это выяснил?

19.58. Как установить табуретку Пол в вашей комнате не очень ровный, зато табуретка совершенно ровная, т. е. нижние концы ее ножек лежат в одной плоскости и образуют квадрат. Как наиболее простым способом установить табуретку, чтобы она не качалась?

19.59. Диагональ кирпича Для того, чтобы найти длину главной диагонали кирпича, т. е. расстояние между наиболее удаленными его вершинами, можно измерить линейкой, например, длину, ширину и высоту кирпича, а затем воспользоваться теоремой Пифагора. Предложите способ измерения линейкой главной диагонали, не требующий никаких вычислений.

19.60. Диаметр проволоки Как измерить с помощью линейки диаметр очень тонкой проволоки?

19.61. Не разматывая рулон Бумажная лента свернута в рулон. Как с помощью линейки определить примерную длину ленты, не разматывая весь рулон целиком?

19.62. Радиус пластинки У вас в руках оказался осколок круглой пластинки. Можно ли по этому осколку определить радиус целой пластинки?

19.63. Объем шара Как с помощью измерительной ленты (сантиметра) определить объем данного шара?

19.64. С маяка Как далеко видно с маяка данной высоты над уровнем моря?

19.65. Радиус шара У вас есть циркуль, линейка, карандаш и бумага. Можете ли вы с их помощью построить отрезок, равный радиусу бильярдного шара, помня, конечно, что прямые линии на сфере рисовать невозможно.

19.66. Наибольший участок Вам нужно отгородить забором фиксированной длины прямоугольный участок. Каким должен быть этот участок, чтобы его площадь была наибольшей?

19.67. Наибольший палисадник У стены дома нужно разбить прямоугольный палисадник, отгородив три его стороны забором фиксированной длины. При каком отношении этих сторон площадь палисадника будет наибольшей?

19.68. Наибольшая коробка Из квадратного листа картона нужно сделать коробку, отрезав от каждого из углов по квадратику (на рис. 138 эти квадратики заштрихованы) и загнув боковые стенки. Каким должно быть отношение высоты коробки к стороне ее основания, чтобы объем коробки был наибольшим?

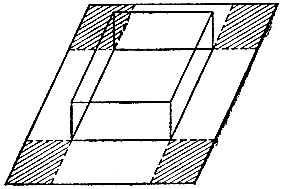
Рис. 138

19.69. Оптимальная форма Все вы видели, как устроен обычный спичечный коробок: он имеет в общей сложности 2 торцевые стенки, 1 крышку, 2 дна и 4 боковые стенки (рис. 139). Какой должна быть форма коробка с фиксированным объемом, чтобы на его изготовление затрачивалось наименьшее количество материала?

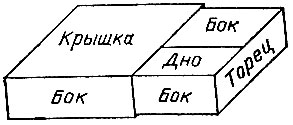
Рис. 139

19.70. Электропроводка Требуется соединить стенной проводкой выключатель и лампочку в зале длиной 30 м, а шириной и высотой по 12 м (рис. 140). Выключатель находится посреди торцевой стены на высоте 1 м от пола, а лампочка находится посреди противоположной стены на расстоянии 1 м от потолка.

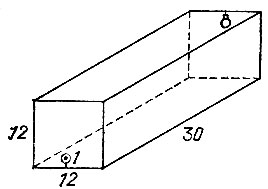
Рис. 140

По какому кратчайшему пути должна проходить проводка?

19.71. Не пробивая стенку На внутренней стенке открытого сверху цилиндрического бункера, сечение которого имеет длину окружности 6 м, а высота которого равна 4 м, находится лампочка на расстоянии 1 м от верха. Напротив лампочки снаружи бункера на высоте 1 м от пола находится выключатель (рис. 141).

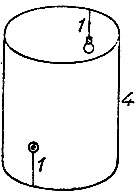
Рис. 141

Какой наименьшей длины провод нужен для проведения стенной проводки между выключателем и лампочкой, не пробивая стенку?

19.72. Не мала ли салфетка? Можно ли завернуть единичный кубик в квадратную салфетку размером 3*3?

19.73. Наибольшая площадь Из прямоугольного треугольника нужно вырезать прямоугольник так, чтобы одна из его вершин совпадала с вершиной прямого угла треугольника, две другие вершины лежали на катетах и одна вершина на гипотенузе, а площадь его была наибольшей.

19.74. Наименьшая площадь Через данную точку внутри угла нужно провести прямую, отсекающую от угла треугольник наименьшей площади. Как это сделать?

19.75. Треугольник из круга Из какого наименьшего бумажного круга можно вырезать треугольник, стороны которого равны 2, 3 и 4?

19.76. Лучший гвоздь В бревно вбито три гвоздя одинаковой длины и массы, но разного сечения: круглый, квадратный и треугольный. Какой из гвоздей держится крепче?

19.77. Не пересчитывая ответ Лист бумаги разорвали на 4 части, затем какие-то из этих частей разорвали на 4 части и т. д. Когда сосчитали общее число частей, то их оказалось то ли 66, то ли 67.

Можно ли, не пересчитывая, уточнить ответ?

19.78. На несколько квадратов Бумажный квадрат требуется разрезать на несколько более мелких квадратов, не обязательно одинаковых. Каким может быть их количество?

19.79. Плитка шоколада Вы хотите разломать плитку шоколада на мелкие квадратные дольки, из которых она состоит. Какое наименьшее число разломов вам для этого потребуется сделать при условии, что разные куски шоколада нужно ломать отдельно?

19.80. Раскраска карты Территория страны разбита на области прямыми линиями. Какое наименьшее число красок необходимо для такой раскраски карты страны, чтобы никакие две области, имеющие общую границу, не оказались одного цвета?

19.81. Огромная дыра Сумеете ли вы разрезать лист из школьной тетради так, чтобы в итоге образовалось кольцо, через которое мог бы свободно пролезть взрослый человек?

19.82. Треугольный паркет Из правильных треугольников можно сложить паркет, т. е. замостить ими всю плоскость без наложений и дыр. А можно ли сложить паркет из произвольных неправильных, но все же одинаковых треугольников?

19.83. Четырехугольный паркет Из каких одинаковых четырехугольников можно сложить паркет?

19.84. Пятью прямыми Проведите 5 прямых, каждая из которых делит заданный прямоугольник на 2 равные части.

19.85. Дырявый прямоугольник Внутри прямоугольного листа бумаги вырезана дырка, имеющая форму параллелограмма (рис. 142). Предложите какой-нибудь способ, как разрезать этот лист на две части одинаковой площади.

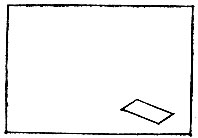
Рис. 142

19.86. Треугольник наизнанку Вы вырезали из цветной бумаги треугольник, да, как выяснилось, у него цветной оказалась не та сторона. Как разрезать этот треугольник на части, чтобы, перевернув их обратной стороной, можно было сложить его снова?

19.87. Площадь пополам Из бумаги вырезан выпуклый четырехугольник. По какой линии, проходящей через данную его вершину, нужно провести разрез, чтобы четырехугольник разделился на две части одинаковой площади?

19.88. Теорема Пифагора На сторонах прямоугольного треугольника построены квадраты (рис. 143). Согласно теореме Пифагора, площадь наибольшего из них равна сумме площадей двух меньших.

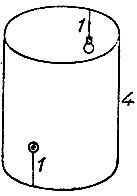
Рис. 143

Попробуйте продемонстрировать этот факт, вырезав два меньших квадрата и разрезав их на такие части, из которых можно составить большой квадрат.

19.89. Плотное заполнение Можно ли ящик размером 20*15*14 заполнить коробками размером 3*5*10 так, чтобы в ящике не осталось пустот и из него не выступали коробки?

19.90. Заготовки для пельменей Из квадратного листа теста размером 8*8 нужно вырезать круги диаметром 1 для изготовления пельменей. Можно ли разместить на этом листе более 64 кругов?

19.91. На почтительном расстоянии Можно ли на круглом поле диаметром 1 км пробурить 125 скважин так, чтобы расстояние между любыми двумя скважинами было больше 100 м?

19.92. Перпендикуляр к диаметру Дана окружность диаметром АВ. Из некоторой точки, не лежащей на прямой АВ, нужно опустить перпендикуляр к этой прямой. Можно ли это сделать, используя только линейку (без делений)?

19.93. Вместо транспортира - линейка С помощью линейки (без делений) с параллельными краями проведите биссектрису данного угла.

19.94. Угол с недоступной вершиной С помощью линейки с параллельными краями проведите биссектрису угла, вершина которого находится за пределами листа бумаги.

19.95. Разделить линейкой без делений При помощи линейки (без делений) с параллельными краями разделите отрезок пополам.

19.96. Центр окружности При помощи линейки с параллельными краями найдите центр данной окружности.

19.97. Двусторонней линейкой Можно ли с помощью двусторонней линейки построить перпендикуляр к данной прямой?

19.98. Линейкой с делениями При помощи обычной линейки с делениями проведите биссектрису данного угла.

19.99. Обыкновенным угольником Найдите центр данной окружности при помощи угольника.

19.100. Найти середину Как с помощью одного угольника разделить данный отрезок пополам?

19.101. Шоколадкой как линейкой Вы положили плитку шоколада на бумагу, обвели ее карандашом и хотите найти точку пересечения диагоналей нарисованного прямоугольника. Можно ли это сделать, используя в качестве линейки ту же плитку, несмотря на то, что ее длины не хватает для проведения диагоналей?

19.102. К недоступному центру На самом краю листа нарисована дуга окружности, центр которой не помещается на бумаге. Через данную точку проведите прямую, проходящую через этот центр.

19.103. Перпендикуляр на краю листа На листе бумаги, имеющем рваный край (рис. 144), с помощью циркуля и линейки восстановите перпендикуляр

к прямой стороне АВ через ее концевую точку А.

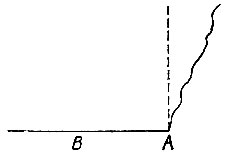
Рис. 144

19.104. Циркулем, но не окружность Можно ли с помощью циркуля нарисовать на бумаге не окружность, а овал?

19.105. Точки на прямой С помощью одного лишь циркуля постройте несколько точек, лежащих на одной прямой с двумя данными точками.

19.106. Одним циркулем Разделите данный отрезок пополам, используя один лишь циркуль.

19.107. Заданные расстояния С помощью одного циркуля по данным двум точкам, расстояние между которыми равно 1, постройте точки, на которых реализуются расстояния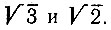

19.108. Найти центр Дана окружность, но не отмечен ее центр. Как найти этот центр с помощью одного лишь циркуля?

19.109. Через недоступную вершину Две данные прямые, пересекаясь, образуют угол, вершина которого находится за пределами листа бумаги. С помощью одной линейки через эту вершину и данную точку проведите прямую.

19.110. Короткой линейкой Вы хотите провести прямую через две данные точки, однако ваша линейка слишком коротка и не достает до двух этих точек одновременно. Нельзя ли обойтись только имеющейся линейкой и все же провести указанную прямую?

19.111. Через кляксу На бумаге нарисован отрезок прямой, которую вы хотите продолжить в определенную сторону с помощью линейки. Однако на вашем пути имеется клякса, не позволяющая непосредственно провести прямую, не испачкав при этом линейку (рис. 145). Предложите способ, как, пользуясь одной линейкой, можно "обогнуть" кляксу и все же построить нужный участок прямой.

Рис. 145