§ 17. Перегибая лист бумаги

Среди множества возможных действий с бумагой особое место занимает операция ее перегибания. Одним из достоинств этой операции является то, что ее можно производить, не имея под рукой никаких дополнительных инструментов - ни линейки, ни циркуля, ни даже карандаша. Этим вы, конечно, неоднократно пользовались, когда складывали из бумаги пилотку, самолет, кораблик и т. п.

Практические свойства бумаги порождают своеобразную геометрию, с элементами которой мы познакомим вас в настоящем параграфе. Роль линий в этой геометрии будут играть края листа и складки, образующиеся при его перегибаниях, а роль точек - вершины углов листа и точки пересечения складок друг с другом или с краями листа. Оказывается, возможности операции перегибаний листа очень велики. То, что они включают в себя всю геометрию одной линейки, не вызывает сомнений. Но они в определенной степени- таят в себе также и возможности циркуля, хотя и не позволяют проводить непосредственно дуги окружности.

Заметим, что при реальной работе с бумагой нужно учитывать следующие обстоятельства. Если складывать лист бумаги в несколько раз, то сами складки получаются все менее и менее четкими из-за того, что настоящая бумага имеет некоторую, пусть незначительную, но ненулевую толщину. Этот эффект иногда начинает проявляться уже при втором перегибании. Следовательно, решая задачи этого параграфа, вы должны беспокоиться о том, чтобы при реализации решений бумагу приходилось складывать по возможности в меньшее число раз. Кроме того, не будем закрывать глаза и на то, что внешний вид бумаги несколько портится от дополнительных складок. Поэтому поищите более экономные в этом смысле построения.

17.1. Почему именно прямая? Каждый, наверное, уже давно привык к тому, что бумага перегибается всегда по прямой линии, а не по окружности и не по какой-нибудь другой кривой. Попробуйте найти причину этого явления.

17.2. Середина отрезка На листе бумаги отмечены две точки А и В. Как с помощью перегибаний этого листа разделить отрезок АВ пополам?

17.3. Перпендикуляр к прямой Как с помощью перегибаний листа бумаги провести прямую, перпендикулярную данной прямой и проходящую через данную точку?

17.4. Параллельная прямая Как с помощью перегибаний листа бумаги провести прямую, параллельную данной прямой и проходящую через данную точку?

17.5. Центр круга Как с помощью перегибаний найти центр вырезанного из бумаги круга? Можно ли найти центр круга, нарисованного на непрозрачной бумаге?

17.6. Пересечение окружности с прямой На листе бумаги проведена прямая, а также даны центр окружности и некоторая точка на ней (сама окружность не нарисована). Как с помощью перегибаний бумаги найти точки пересечения воображаемой окружности с проведенной прямой?

17.7. Построения в треугольнике Из бумаги вырезан треугольник. Укажите, как с помощью перегибаний найти следующие линии и точки этого треугольника: биссектрису данного угла; высоту, опущенную из данной вершины (если углы при двух других вершинах острые); медиану, проведенную к данной стороне; центр вписанной окружности- центр описанной окружности (для остроугольного треугольника).

17.8. Выравнивание краев бумаги У вас в руках оказался лист бумаги неправильной формы, а вы хотите с помощью перегибаний получить из него бумажный прямоугольник. Один из простейших способов сделать это состоит в последовательном проведении сначала какой-либо прямой АВ, затем перпендикуляра ВС к ней, затем перпендикуляра CD к полученной прямой и, наконец, перпендикуляра DA к прямым CD и АВ (рис. 87). Однако если проводить перпендикуляры так, как это описано в решении задачи 17.3, то слишком много бумаги уйдет в отходы. Дело в том, что проведение перпендикуляров описанным способом предполагает наличие достаточно больших участков дайной прямой как с одной, так и с другой сторону отданной точки (иначе точность построения сильно падает: таким образом на рис. 87 перпендикуляр к прямой АВ через точку В точно провести практически не удается).

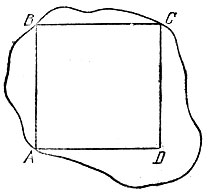
Рис. 87

Придумайте другой способ проведения перпендикуляров, пользуясь которым можно свести расход бумаги при выравнивании ее краев к минимуму (например, реализовать построение прямоугольника ABCD, изображенного на рис. 87).

17.9. Из прямоугольника квадрат Из бумаги вырезан прямоугольник. Получите из него квадрат со стороной, равной меньшей стороне прямоугольника.

17.10. Из прямоугольника треугольник Из бумаги вырезан прямоугольник. Укажите способ получения из него различных равнобедренных треугольников и, в частности, равностороннего треугольника.

17.11. Треугольник в квадрате Из бумаги вырезан квадрат ABCD. Как при помощи перегибаний вписать в него равносторонний треугольник AEF, имеющий с квадратом ровно одну общую вершину А (рис. 88).

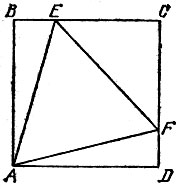
Рис. 88

17.12. Из треугольника шестиугольник Из листа бумаги, имеющего форму равностороннего треугольника, с помощью перегибаний нужно получить правильный шестиугольник. Как это сделать?

17.13. Из квадрата восьмиугольник Из листа бумаги, имеющего форму квадрата, с помощью перегибаний нужно получить правильный восьмиугольник. Как это сделать?

17.14. Сумма углов треугольника С помощью перегибаний произвольного бумажного треугольника продемонстрируйте тот факт, что сумма углов при его вершинах равна 180°.

17.15. "Живая закладка" Если вам понадобилось чем-нибудь заложить страницу в записной книжке так, чтоб закладка торчала, но под рукой нет никакого подходящего предмета, то подумайте над вопросом, нельзя ли перегнуть саму страницу, нигде не разрывая ее, чтобы в результате какой-то ее краешек торчал из закрытой записной книжки.

17.16. Можно ли увеличить периметр? Можно ли сложить многоугольник, вырезанный из бумаги, так, чтобы периметр полученной фигуры оказался больше, чем периметр исходного многоугольника?

17.17. Квадрат из полоски Из бумажной полоски шириной 1 с помощью нескольких перегибаний получите квадрат, у которого диагональ равна 2.

17.18. Шестиугольник из полоски Из бумажной полоски шириной 1 с помощью перегибаний получите правильный шестиугольник, у которого расстояние между параллельными сторонами равно 2.

17.19. Загадочный узел Попробуйте завязать бумажную полоску с параллельными краями узлом так, чтобы после ее стягивания и разглаживания в узле образовался пятиугольник ABCDE, изображенный на рис. 89. Докажите, что этот пятиугольник правильный.

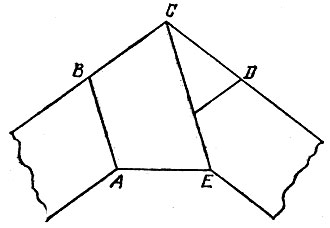
Рис. 89