Решения

18.1. При несовпадении двух проведенных отрезков АВ можно сделать вывод о непригодности линейки для проведения прямых линий: ведь если бы проведенные отрезки были действительно прямыми, то отрезки были действительно прямыми, то они должны были бы совпасть (через точки А и В проходит ровно одна прямая). Если же проведенные отрезки совпадут, то это еще не будет означать, что линейка и в самом деле имеет ровный край. На рис. 112 изображена линейка с неровным краем, которая успешно пройдет проверку, описанную в условии задачи.

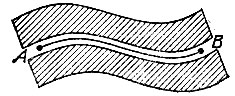
Рис. 112

18.2. Исправление описанной в условии задачи 18.1 проверки состоит в том, чтобы поворот линейки на 180° по плоскости бумаги заменить ее поворотом в пространстве вокруг прямой АВ. Если после такой исправленной проверки проведенные отрезки АВ совпадут, то линейка имеет ровный край. Действительно, предположив, что какая-то точка С первой из проведенных линий АВ не лежит на прямой АВ, мы получим, что точка С, симметричная точке С относительно прямой АВ, будет лежать на второй из проведенных линий АВ (рис. 113). При этом точки С и С не совпадут, что будет выявлено при исправленной проверке.

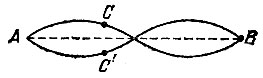
Рис. 113

18.3. Линейку можно повернуть по плоскости бумаги на 180°. В случае параллельности* краев линейки это приведет к совпадению двух проведенных отрезков CD (через точку С проходит ровно одна прямая, параллельная прямой АВ). Если же края линейки не параллельны, то прямые АВ и CD пересекаются в некоторой единственной точке О, лежащей где-то очень далеко от точек А, В, С, D. После описанного поворота линейки точка О перейдет в точку О', которая в случае совпадения двух проведенных отрезков CD будет являться еще одной точкой пересечения прямых АВ и CD, что невозможно. Таким образом, совпадение отрезков CD означает параллельность краев линейки.

18.4. Проведем прямую АВ и, приставив к ней угольник одним катетом, восставим перпендикуляр CD к прямой АВ в некоторой точке и рис. 114). Повернув угольник по плоскости бумаги на 90° вокруг точки С и приставив к прямой АВ угольник другим катетом, восставим еще раз перпендикуляр CD к этой прямой в точке С. Если два проведенных отрезка CD совпадут, то угольник имеет прямой угол, а если не совпадут, то используемый для построений угол не является прямым.

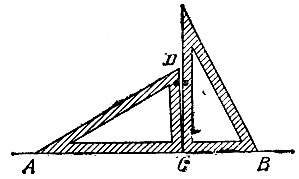
Рис. 114

18.5. Пусть мы проверяем треугольник ABC. Для установления равенства АВ = ВС достаточно перегнуть треугольник по биссектрисе угла ABC (это делается путем совмещения луча ВА с лучом ВС) и определить, совмещаются ли при этом точки А и С. Аналогично проверяются равенства ВС = АС и АВ = АС.

18.6. Данный кусок материи не обязательно имеет форму квадрата. Действительно, всем описанным в задаче условиям будет удовлетворять любой ромб, так как обе его диагонали являются его осями симметрии. Кстати, описанную в задаче процедуру можно рассматривать именно как проверку того, является ли четырехугольник ромбом.

18.7. Данный кусок материи не обязательно имеет форму квадрата. Действительно, всем описанным в задаче условиям будет удовлетворять любой прямоугольник, так как обе линии, соединяющие середины его противоположных сторон, являются его осями симметрии. Кстати, описанную в задаче процедуру можно рассматривать именно как проверку того, является ли четырехугольник прямоугольником.

18.8. Необходимо перегнуть четырехугольный кусок материи два раза. В самом деле, одного перегибания явно недостаточно для проверки того, является ли четырехугольник квадратом, так как наличие у него не только одной, а даже двух осей симметрии еще не позволяет утверждать, что четырехугольник есть квадрат (см. задачи 18.6 и 18.7). С другой стороны, если четырехугольник ABCD симметричен относительно диагонали АС и относительно прямой EF, проходящей через середины сторон АВ и CD (рис. 115), то он является квадратом. Действительно, применяя в определенном порядке указанные симметрии, получаем равенства AB = AD = BC = CD и ∠ ABC = ∠ BAD = 90°, из которых следует, что четырехугольник ABCD является ромбом и прямоугольником, т. е. квадратом.

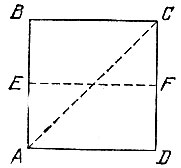
Рис. 115

18.9. Гарантии того, что кусок материи имеет форму круга, дать нельзя, если нам не известно, по каким именно линиям производились сгибания материи. Например, если n этих линий выбраны так, как указано на рис. 116, т. е. делят полный угол на 2n одинаковых углов, то кусок материи может оказаться как правильным 2n-угольником, так и криволинейной фигурой, образованной поворотами какой-нибудь кривой линии типа ABC на углы, кратные углу АОС.

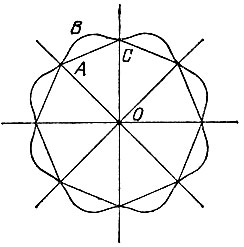
Рис. 116

Однако, как это ни удивительно, для проверки того, имеет ли данный кусок материи форму круга, достаточно убедиться, что он имеет всего лишь две оси симметрии, от которых требуется только, чтобы угол между ними измерялся иррациональным числом градусов.

18.10. Перегнув материю поперек тех двух ее краев, параллельность которых подлежит проверке, мы можем совместить один край ЕА с его продолжением ЕВ по общей их части (рис. 117), а затем проверить, совместился ли при этом другой край FC с его продолжением FD по общей их части (мы подразумеваем, что линия перегиба EF пересекает оба исследуемых края материи). Если на другом крае произошло совмещение, то прямые АВ и CD параллельны, так как перпендикуляр EF к прямой АВ (углы AEF и BEF равны в силу их симметрии) в этом случае является одновременно и перпендикуляром к прямой CD (углы CFE и DFE также равны в силу их симметрии). Если же на другом крае совмещения не произошло, то прямые АВ и CD не параллельны, так как отрезок EF в этом случае перпендикулярен прямой АВ, но не перпендикулярен прямой CD.

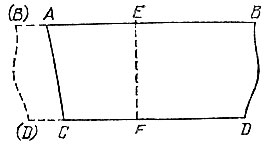
Рис. 117

Теперь найдем указанным способом все пары параллельных противоположных сторон данного четырехугольного куска материи. Если таких пар окажется две, то этот кусок имеет форму параллелограмма, если одна - то трапеции, а если ни одной - то ни то, ни другое. 18.11, Пусть угол А является наибольшим углом треугольника ABC (определить его можно, например, описанными ниже перегибаниями, позволяющими непосредственно сравнивать по величине любые два угла треугольника). Перегнем материю по линии EF (рис. 118) так, чтобы точка С совместилась с точкой А.

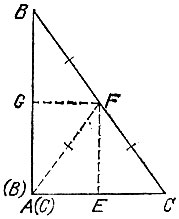
Рис. 118

Перегнем материю, не разворачивая после первого перегиба, по линии FG так, чтобы в результате луч FB совместился с лучом FC. Тогда если после этих двух перегибов точки В и С совместились, то угол А прямой, если отрезок FC оказался длиннее отрезка FB, то угол А острый (рис. 119), а если наоборот, то угол А тупой (рис. 120).

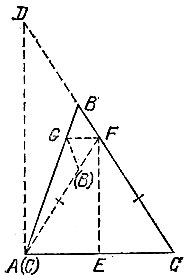
Рис. 119

Докажем последнее утверждение. Если точки В и С совместились, то AF = BF = CF и поэтому точки А, В и С лежат на окружности с центром F и диаметром ВС, откуда угол САБ прямой. Если AF = CF = BF, то возьмем на луче FB точку D, удовлетворяющую равенству DF = CF и, следовательно, по доказанному образующую прямой угол DAC. В случае BF<DF имеем ∠ ВAС<∠ DAС = 90°, а в случае BF&362;Df имеем ∠ BAC > ∠ DAC = 90°, что и требовалось доказать.

Рис. 120

18.12. Чтобы убедиться в вертикальности шеста (рис. 121), достаточно проверить, что шест находится в одной плоскости с некоторой вертикальной линией, а также в одной (другой) плоскости с некоторой другой вертикальной линией. Указанную проверку можно осуществить с помощью отвеса (бечевки с грузиком на конце): если расположить его перед собой так, чтобы верхние концы отвеса и шеста оказались на одной линии с глазом, то линии отвеса и шеста должны зрительно совпасть.

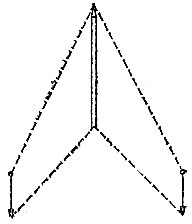
Рис. 121

Для обоснования этого способа проверки заметим, во-первых, что вертикальный шест должен лежать в одной плоскости с любой вертикальной прямой, а, во-вторых, если две параллельные прямые лежат в двух пересекающихся плоскостях соответственно, то эти прямые параллельны и линии пересечения плоскостей.

18.13. Проверка основана на свойстве плоскости содержать вместе с любыми двумя точками прямую, через них проходящую. Однако описанная проверка не позволяет отличить выпуклую поверхность от ровной, так как и у той, и у другой поверхности не будет никакого просвета с ниткой (просвет был бы возможен, если бы нитка могла пройти сквозь поверхность). Для исправления этой проверки можно предложить контролировать себя легким поднятием одного конца нитки: если при этом нитка прикасается к плоскости только другим своим концом, то выпуклости не наблюдается, если же она прикасается где-то в промежуточной точке между концами, то выпуклость есть (рис. 122).

Рис. 122

18.14. Будем предполагать, что стены в комнате вертикальны, а пол горизонтален (рис. 123). Отложим по нижнему краю стен от точки А, лежащей на линии их пересечения, отрезки АВ и АС длиной 3 и 4 произвольных единицы, например, дециметров. Тогда угол ВАС, представляющий собой линейный угол двугранного угла между стенами, будет прямым тогда и только тогда, когда длина отрезка ВС равна 5 единицам (если вас заинтересует вопрос о существовании других целочисленных прямоугольных треугольников, то читайте § 7).

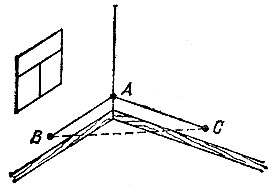
Рис. 123

18.15. Будем предполагать, что стены коридора вертикальны. Выберем у нижнего края каждой из двух стен по одной точке А и В и отложим от этих точек вдоль нижнего края стен (рис. 124) в одном направлении отрезки BD к АС одинаковой длины, например длины АВ. Тогда если отрезки АВ и CD равны, то стены параллельны, а если эти отрезки не равны, то и стены не параллельны.

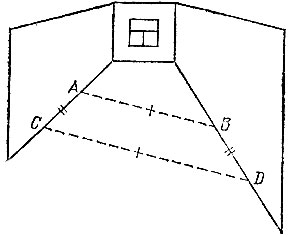
Рис. 124

В самом деле, из равенств AB = CD и AC = BD следует, что четырехугольник ABDC - параллелограмм, откуда стороны АС и BD параллельны. С другой стороны, если отрезки АС и BD параллельны, то из равенства AC = BD следует, что четырехугольник ABDC - параллелограмм и АВ = СD. Наконец, так как плоскости стен вертикальны, то их параллельность имеет место тогда и только тогда, когда они пересекаются с невертикальной плоскостью пола по параллельным прямым.

18.16. Действия, описанные в п. а), позволяют однозначно установить параллельность двух данных сторон AD и ВС четырехугольника ABCD. Действительно, если AD||BC, О - точка пересечения диагоналей, Е - середина отрезка AD, F - точка пересечения прямых ЕО и ВС (рис. 125), то ∠ OAD = ∠ OCB, ∠ ODA = ∠ OBC, ∠ AOE = ∠COF, ∠ DOE = ∠BOF, откуда получаем, что треугольники АОЕ и COF, а также треугольники DOE и BOF подобны. Поэтому имеем пропорции

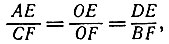
и так как AE = DE, то CF = BF, Это означает, что отрезок EF, соединяющий середины параллельных сторон AD и СВ, проходит через точку пересечения диагоналей четырехугольника ABCD.

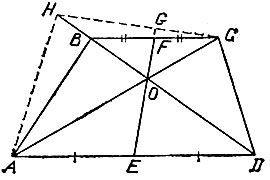
Рис. 125

Докажем теперь, что отрезок EG, соединяющий середины непараллельных сторон AD и СН, не проходит через точку О пересечения его диагоналей четырехугольника ADCH (рис. 125). Пусть, напротив, этот отрезок проходит через точку О. Тогда через точку С проведем прямую, параллельную прямой AD, до пересечения в точке В с прямой DH. По доказанному выше имеем CF = BF, а с другой стороны, CG = GH, поэтому FG - средняя линия треугольника СВН, которая не может пересекать соответствующую ей прямую ВН в точке О, что противоречит предположению.

Докажем, что действия п. б) условия задачи также однозначно отвечают на вопрос о параллельности сторон AD и СВ четырехугольника ABCD, В самом деле, пусть точка G - середина диагонали АС. Тогда отрезок EF, соединяющий середины сторон АВ и DC, равен полусумме сторон AD и СВ, т. е. сумме отрезков EG и FG - средних линий треугольников АСВ и ADC, в том и только в том случае, если точка G принадлежит отрезку EF (рис. 126). Поскольку EG||BC и FG||AD, то последнее условие равносильно параллельности отрезка EF сразу двум отрезкам ВС и AD, т. е. параллельности самих сторон AD и СВ, что и требовалось доказать.

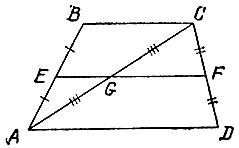
Рис. 126

Таким образом, для проверки того, что данный четырехугольник ABCD является трапецией, достаточно соединить отрезком середины двух его противоположных сторон и проверить ровно одно из двух условий: либо этот отрезок равен полусумме двух других сторон четырехугольника (которые тогда как раз и будут основаниями трапеции, а в противном случае ими будут другие стороны), либо этот отрезок проходит через точку пересечения диагоналей. Если оба условия одновременно окажутся выполненными, то четырехугольник ABCD есть не трапеция, а параллелограмм.

18.17. Заметим, что если четырехугольник ABCD является параллелограммом, то все свойства, перечисленные в пп. а), б), в) условия задачи, для него выполнены. Пусть теперь AB = CD и AD = BC (рис. 127), тогда треугольники ABC и ADC равны по трем сторонам, откуда

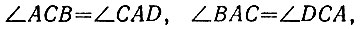
т. е. противоположные стороны четырехугольника ABCD попарно параллельны. Итак, свойство а) является и необходимым, и достаточным для параллелограмма.

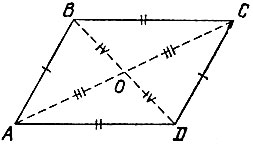
Рис. 127

О свойстве б) этого сказать нельзя, поскольку оно выполняется не только для параллелограмма, но и для любой равнобедренной трапеции (докажите, что ни для каких других выпуклых четырехугольников оно не выполняется).

Наконец, свойство в) является достаточным для того, чтобы объявить четырехугольник ABCD параллелограммом, поскольку равенство отрезков АО и СО, а также ВО и DO (рис. 127) влечет за собой равенство треугольников АОВ и COD, а также AOD и ВОС, откуда в свою очередь вытекает равенство противоположных сторон четырехугольника.

18.18. Для ответа на поставленный в задаче вопрос достаточно проверить, что замкнутая ломаная ABCDA ограничивает четырехугольник, который, согласно определению ромба, уже и будет ромбом. Действительно, так как равнобедренные треугольники ABC и ADC равны, то точки В и D находятся по разные стороны относительно прямой АС (иначе эти точки просто совпали бы друг с другом). Поэтому отрезок АВ не пересекается с отрезком CD, а отрезок AD не пересекается с отрезком ВС, т. е. ломаная ABCDA несамопересекающаяся, а, значит, ограничивает настоящий ромб ABCD.

18.19. Свойство, описанное в п. а), не является достаточным для того, чтобы объявить четырехугольник прямоугольником, поскольку это свойство выполняется также и для любой равнобедренной трапеции (докажите, что ни для каких других выпуклых четырехугольников оно не выполняется).

Свойства б) и в) достаточны, чтобы объявить четырехугольник прямоугольником. Действительно, из попарного равенства противоположных сторон четырехугольника вытекает, что он является параллелограммом (см. задачу 18.17), откуда получаем, что его диагонали делятся точкой их пересечения пополам, причем если сами диагонали равны, то равны и их половинки. Итак, из свойства б) вытекает свойство в). Наконец, если для четырехугольника выполнено свойство в), то точка О пересечения его диагоналей равноудалена от его вершин. Это означает, что точка О является центром описанной около четырехугольника окружности, а его диагонали являются диаметрами этой окружности, на которые опираются вписанные углы при вершинах четырехугольника. Следовательно, все эти углы прямые, что и требовалось доказать.

18.20. Заметим, что для квадрата выполняются все свойства а), б), в), перечисленные в условии задачи. Однако свойство а) выполняется не только для квадрата, но и вообще для любого ромба (и только для него, согласно задаче 18.18). Свойство в) выполняется также и для любой равнобедренной трапеции, у которой одно из оснований равно боковой стороне (докажите, что ни для каких других выпуклых четырехугольников оно не выполняется). Наконец, если для четырехугольника выполнено свойство б), то этот четырехугольник является ромбом (см. задачу 18.18) и прямоугольником (см. задачу 18.19) одновременно, а значит, и квадратом.

18.21. Вписанный равносторонний многоугольник обязательно является правильным (см. задачу 15.1), а вот описанный - не обязательно. Например, любой ромб, в который всегда вписывается окружность (так как его центр симметрии равноудален от всех четырех сторон), является равносторонним, но не правильным четырехугольником.

Полезно знать все же, что для правильности описанного нечетноугольника достаточно (и, разумеется, необходимо), чтобы он был равносторонним. Например, вершины А и С (расположенные через одну на рис. 128) равностороннего описанного пятиугольника равноудалены от центра О вписанной в него окружности. Действительно, так как АВ = ВС и DB = BE (отрезки касательных к окружности, проведенных из одной точки В, равны), откуда AD = EC, и раз OD = OE и ∠ ADO = ∠ CEO = 90°, то треугольники ADO и CEO равны. Двигаясь от вершины А через одну, мы перечислим все вершины пятиугольника, которые, таким образом, будут все равноудалены от точки О. Поэтому указанный пятиугольник одновременно является вписанным и, стало быть, правильным.

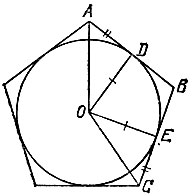
Рис. 128

18.22. Пятиугольник с равными диагоналями не обязательно правилен. Это утверждение подтверждается пятиугольником AEDCB, построенным следующим образом (рис. 129): пусть в равнобедренном треугольнике ADB угол при вершине D меньше 36°, тогда проведем перпендикуляры к прямой АВ, удаленные от точки D на расстояние, равное половине AD, и выберем на них точки С и Е, удаленные от точек А и В соответственно на расстояние AD, В построенном пятиугольнике все пять диагоналей равны между собой (по построению они равны диагонали AD), однако сам пятиугольник не является правильным, поскольку угол между диагоналями, выходящими из одной вершины правильного пятиугольника, равен 36°, а у нас получилось неравенство

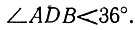
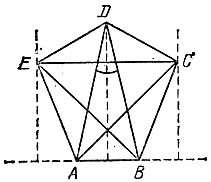
Рис. 129

Заметим, что более убедительным, хотя и менее строгим примером может служить вырожденный пятиугольник AEDCB со слившимися вершинами А и В, изображенный на рис. 130 и полученный из равностороннего треугольника АЕС добавлением еще одной вершины D, удаленной от вершины А на расстояние АС, и раздвоением вершины А на две вершины А и В.

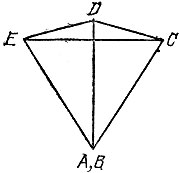
Рис. 130

Приемом построения вырожденных контрпримеров мы воспользуемся при решении следующих задач, а при желании вы сможете сами слегка подправить построения так, чтобы они были невырожденными.

18.23. Наименьшее число равных диагоналей, необходимых для проверки правильности равностороннего пятиугольника ABCDE, равно трем. Действительно, двух равных диагоналей для этого недостаточно: пример вырожденного пятиугольника, превратившегося в трапецию с равными диагоналями BD и СЕ, изображен на рис. 131.

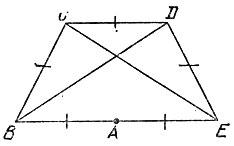
Рис. 131

Если же у равностороннего пятиугольника ABCDE равны три диагонали, скажем AC, BD и СЕ (а на самом деле любые три диагонали - попробуйте доказать это самостоятельно), из равенства треугольников ABC, BCD и CDE (по трем сторонам) вытекает равенство углов пятиугольника при вершинах В, С и D (рис. 132). Кроме того, из равенства треугольников ABD и ACD (по трем сторонам) имеем ∠ BAD = ∠ CDA, откуда с учетом равнобедренности треугольника AED получаем равенство углов пятиугольника при вершинах А и D. Аналогично доказывается равенство углов при вершинах В и Е, т. е. равенство всех углов и, значит, правильность пятиугольника ABCDE.

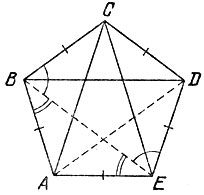
Рис. 132

18.24. Условие а) в дополнение к тому, что три главные диагонали равностороннего шестиугольника пересекаются в одной точке, не обеспечивает его правильности. Например, вырожденный шестиугольник ABCDEF, превратившийся в прямоугольник и изображенный на рис. 133, удовлетворяет всем перечисленным условиям, но не является правильным.

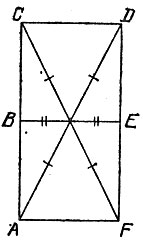
Рис. 133

Аналогично обстоит дело и с условием в), для которого контрпримером служит вырожденный шестиугольник ABCDEF, превратившийся в треугольник и изображенный на рис. 134 (в нем главные диагонали AD, CF и ЕВ равны и пересекаются в одной точке, неглавные диагонали образуют равносторонние треугольники АСЕ и BDF).

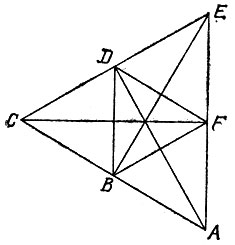
Рис. 134

Если же выполнено условие б), то около шестиугольника можно описать окружность с центром в точке пересечения его главных диагоналей, а коль скоро сам шестиугольник является еще и равносторонним, то он обязательно правильный (см. задачу 18.21).

18.25. Наименьшее число диагоналей, которое нужно проверить, равно четырем. В том, что трех диагоналей недостаточно, можно убедиться непосредственным перебором различных случаев. Если же в равностороннем шестиугольнике ABCDEF равны четыре неглавные диагонали АС, СЕ, ЕА и BD (рис. 135), то этот шестиугольник правильный. Действительно, углы шестиугольника при вершинах В, С, D и F равны в силу равенства треугольников ABC, BCD, CDE и EFA (по трем сторонам), а углы при вершинах С, Е и А также равны, поскольку они представляют собой одинаковые суммы углов (один из которых есть угол при вершинах С, Е или А равностороннего треугольника АСЕ, а два других являются углами при основаниях одинаковых равнобедренных треугольников АВСУ CDE или EFA). Таким образом, все углы равностороннего шестиугольника ABCDEF равны; следовательно, он правильный.

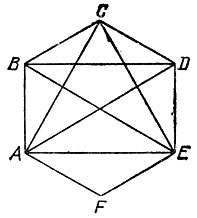
Рис. 135