Схолия Десятая,

Схолия Десятая,

замечательная как своей непревзойденной краткостью, так и весьма скромными размерами сообщаемых ею фактов, на один из коих потребовалось всего-навсего: одна странная вещица, которую Илюша второпях принимает за бильярд, три шахматные доски, одно маковое зернышко, восемьдесят квадриллионов нулей и очень миленькая девушка, некая Альфа Ц. (известная тем, что когда бы на нее ни поглядели, всегда кажется, что она на пять лет моложе того, что есть на самом деле), после чего читатель узнает кое-что о славе Архимедовой, которой не были страшны долгие века, и об одной отважной путешественнице.

Радикс опустил свой длинный нос пониже и довольно лукаво посмотрел на Илюшу. Тому после испанской задачки ничего другого не оставалось, как сделать вид, что он этого не замечает.

- Нет, - сказал мальчик, - ты мне все-таки лучше про Бриарея...

- 170 -

- Про Бриарея рассказ будет не очень длинный. Бриарей был, по древнему греческому мифу, одним из детей Урана - неба и Геи - земли, от которых родились титаны, гекатонхойры (что значит сторукие) и одноглазые циклопы. С одним из этих последних встретился Одиссей, как ты, вероятно, знаешь (а не знаешь, так возьми "Одиссею" в переводе Шуковского и узнаешь). Бриарей и был одним из гекатонхейров, которые в мифах олицетворяли грозные силы разбушевавшейся морской стихии. Титаны олицетворяли собой первобытные силы природы в их совокупности, а циклопы - явления небесной грозы: гром, молнию и заодно уж извержения вулканов и землетрясения. Все эти титаны были до того страшны, что собственный отец заточил их в Тартар. А потом, когда титаны восстали против Зевса, он победил их с помощью гекатонхейров и циклопов. Миф этот связан с осадой Сиракуз римлянами, потому что Марцелл, предводитель римского войска, однажды сказал, объясняя своим воинам причины неудачных штурмов Сиракуз, что победить Архимеда, "этого Бриарея геометрии", почти невозможно. Вот поэтому-то мы иногда здесь о нем и вспоминаем.

- Значит, - сказал Илюша, - Бриарей был великан?

- В этом роде, - отвечал Радикс. - Но мы здесь видали и не таких великанов.

- Это ты про Великую Теорему?

- Нет. Есть великаны и попроще, но такого удивительного роста, что невольно диву даешься. Мы с тобой сейчас говорили о мифах. Эти прекрасные, поистине высокопоэтические создания народного гения сохранили нам не только образы древнего искусства, но и замечательные мысли. Возможно, мы снова вспомним нашего сиракузского Бриарея. Люди с давних времен всегда интересовались большими числами. В трудах индийских математиков, поскольку они отразились в легендах и поэмах древней Индии, мы встречаем не просто упоминания о больших числах, но суждения о том, как их строит мысль человеческая, какие числовые громады можно построить, исходя из довольно простых принципов. Так, в одной из древнейших книг Индии рассказывается, каким образом могут быть уложены камни при постройке некоей стереометрической фигуры. Счет начинается с десяти тысяч, затем это число последовательно увеличивается путем умножения его на десять, и девятое число из этого ряда уже довольно велико: десять в двенадцатой степени. Мы теперь называем его триллионом- это миллион миллионов. Чтобы как-нибудь представить себе эту "крошку", вспомним вот о чем. Самая близкая к нам звезда, не принадлежащая к нашей Солнечной системе, называется Альфа Центавра. Ты, наверное, знаешь, что обычно отдельные звезды созвездия называются греческими буквами.

- 171 -

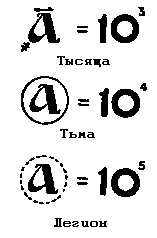
Так вот, Альфа Центавра находится от нас на расстоянии сорока триллионов километров. Свет в одну секунду пролетает триста тысяч километров. В году свыше тридцати миллионов секунд; следовательно, свет этой звезды должен идти к нам примерно четыре с половиной года. Довольно долго, не правда ли? Допустим, что у нас с тобой будет самолет, который летает со скоростью тысяча километров в час.

Для КРУГЛОГО счета будем считать, что в году девять тысяч часов. Тогда за год он пролетит девять миллионов километров, за сто лет – девятьсот миллионов километров, то есть еле приблизится к биллиону. Таким образом, чтобы пролететь триллион километров, нашему самолету придется лететь, не останавливаясь, сто тысяч лет с лишним. Ты видишь, что триллион- это довольно почтенное число.

- Да уж действительно! А скажи, пожалуйста, ведь биллион не редко называют еще миллиардом, так нельзя ли на этом основании назвать триллион биллиардом?

- Нет, такого названия не существует. Ну, слушай дальше. Мысль древнеиндийских математиков и поэтов на этом не остановилась. В поэме Рамаяна описывается воинственный бог Сугрива, который ведет страшное обезьянье войско. Число хвостов в этих ужасающих полчищах начинает исчисляться обезьяньими дивизиями, в каждой из которых ты находишь, ни много ни мало, сто миллионов непобедимых мартышек. Затем эти дивизии объединяются во все более и более крупные соединения, и в конце концов во всей этой бесподобной армии насчитывается 10³⁸ мохнатых богатырей. Что такое 10³⁸ по нашей системе? Если мы назовем с тобой 10³³ децильоном, то дальше счет пойдет так:

10³³ ....... децильоны

10³⁶ ....... тысячи децильонов

10³⁹ ....... миллионы децильонов

10⁴² ....... биллионы децильонов

Как видишь, хвостов в распоряжении этого индийского вояки было вполне удовлетворительное количество.

Кстати, скажу тебе вот еще что. В старинных русских рукописях тоже имеются рассуждения о весьма больших числах.

В одной рукописи приводится число, о котором говорится, что "больше сего числа несть человеческому разуму разумети".

- 172 -

Оно именуется "колодой" и равняется 10⁸, то есть сотне миллионов. Однако это еще не всё. В другой рукописи есть указание на то, что, кроме обычной системы, которая заканчивается колодой, существует еще и иная система, называемая "числом великим словенским", и там уже "последнее" число равняется 10⁴⁸. А теперь обрати внимание на то, что эти индийские поэмы, как и их отражения в старинных русских рукописях, никогда не называют большое число сразу, а показывают, как путем постепенного увеличения вполне обозримого числа мы получаем числа, которые уже превосходят наше воображение. Есть еще одна замечательная индийская легенда о том, как царевич Бодхисатва сватался к дочери царя Дандапани и какими вопросами испытывал царевича премудрый Арджуна. Речь идет о системах счисления и о том, каковы примерно размеры получаемых при этом чисел. Эта прекрасная сказка очень напоминает одно замечательное творение нашего с тобой любимца Архимеда. Оно построено по тому же принципу, как и сказка об индийском царевиче. Хочешь послушать?

- Да-да! - сказал Илюша. - Про Архимеда мне все очень интересно.

- Отлично. Дело было в третьем веке до нашей эры. Архимед в этом сочинении, которое написано в форме послания к сиракузскому царю Гелону, идет примерно тем же путем, каким шли индийские математики. Он показывает на очень хорошем примере, что человек в рассуждениях может составить числа, превышающие всякий, даже самый необъятный на первый взгляд пример. Архимедов "Счет песчинок" (так называется это его сочинение) начинается следующими словами: "Некоторые - о царь Гелон! - думают, что число песчинок бесконечно. Не только тех песчинок, что находятся вблизи Сиракуз и по всей Сицилии, но и всех тех, что рассеяны по всем обитаемым и необитаемым странам земли. Другие полагают, что число это не бесконечно, но невозможно определить словесно количество, которое превышало бы число всех этих песчинок". Архимед утверждает, что мнения эти неправильны, и опровергает их таким образом. Возьмем песчинку и предположим, что в одном маковом зернышке находится 10⁴, или десять тысяч таких песчинок. Не правда ли это будет довольно маленькая песчинка?

- Ясно, - отвечал Илюша, прямо пылинка.

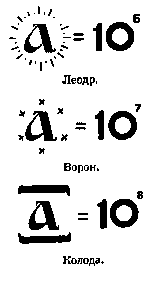
- 173 -

- Далее Архимед говорит, что один палец равен сорока диаметрам макового зернышка, а стадия (греческая мера длины, которая равна примерно ста шестидесяти метрам) меньше десяти тысяч пальцев. Затем он говорит, что если мы возьмем шар с диаметром в одну стадию, то объем его будет меньше, чем объем куба, ребро которого равно одной стадии, что очевидно, ибо такой шар можно вписать в такой куб. Из этого он заключает, что в шаре с диаметром в одну стадию не может заключаться песчинок более нежели 10²¹, то есть более секстильона. Ясно, что объем этого шара менее, чем 104 кубических пальцев, он меньше, чем 40³ • 10¹² зернышек мака, а следовательно, меньше, чем 10⁴ • 40³ • 10¹², или 64 • 10¹⁹, песчинок, а стало быть, он меньше, чем секстильон, равный 10²¹.

Далее он полагает, что если построить шар с диаметром, равным диаметру Солнечной системы, который, как он полагает, меньше 10¹⁰ стадий, то объем этого шара будет менее 10³⁰ кубических стадий, а следовательно, в нем будет заключаться менее, чем 10⁵¹ песчинок, или, по нашей с тобой системе, менее квинтильона децильонов. Наконец, Архимед строит шар с радиусом, равным расстоянию от Земли до неподвижных звезд, которое, по его мнению, менее десяти тысяч диаметров Солнечной системы, и утверждает, что в таком шаре будет заключаться менее 10⁶³ песчинок, или, по нашим с тобой обозначениям, менее нонильона децильонов. Может быть, тебе эта величина станет немного яснее, если я скажу, что в переводе на современные меры объем этой сферы Архимеда менее нежели 5 • 10⁵⁴ кубических сантиметров.

Но Архимед не употреблял позиционной системы, как не пользовался он и показателями степени. Он строит для этого рассуждения свою систему чисел, начиная с греческого числа "мириада", которое равно десяти тысячам, то есть 10⁴. Тогда числа до мириады он называет первыми числами, затем идет мириада мириад, или 10⁸, которая будет единицей вторых чисел. Мириада мириад вторых чисел, или 10¹⁶, будет единицей третьих чисел, и так далее. И вот теперь оказывается, что для того, чтобы определить, сколько песчинок будет в сфере, радиус которой равен расстоянию от Земли до неподвижных звезд, достаточно взять число, которое будет менее тысячи мириад восьмых чисел Архимеда.

Таким образом, Архимед на очень несложном и очень ярком примере показал, что человеческая способность последовательно строить числа легко справляется с величинами, для которых трудно подобрать пример, который что-нибудь говорил бы нашим чувствам. Заметь, что Архимед нигде не определяет точно своих чисел. Он ограничивается тем, что указывает только на то, что искомое число не может превышать некоторой определенной величины. Таким образом, он нам указывает на то, что называется порядком величины. Мне кажется, да ты и сам можешь легко догадаться (уже не маленький!), что большего в таком рассуждении и не надо.

- 174 -

- Да, уж действительно! - промолвил Илюша. - Я раньше думал, что это ужасно большое число, знаешь, вот в этой задаче, где надо сосчитать, сколько зерен будет лежать на шахматной доске в шестьдесят четыре квадрата, если на первый квадрат положить одно зернышко пшеницы и на каждую следующую клетку класть в два раза больше. Но там совсем не так много получается.

- Да. Для обыкновенной шахматной доски получается число порядка десятков квинтильонов. Если взять стоклеточную доску, на которой играют в так называемые "польские шашки", то тогда число зерен доберется до нонильонов. А если взять доску еще побольше, у которой не десять полей с каждой стороны, а четырнадцать, и всего будет сто девяносто шесть полей, то вот тогда мы как-нибудь уж доползем до сотен септильонов децильонов.

- Как скоро все-таки растет! - воскликнул Илюша.

- Да, - отвечал Радикс, - растет недурно. Что же касается Архимеда, то он останавливается на числе, которое можно записать так:

10^8•1016

и которое представляет собой единицу с восьмьюдесятью квадриллионами нулей. Если это число написать на бумажной ленте, умещая по пятисот нулей на одном метре, то есть писать очень мелко и убористо, то на одном километре ленты мы напишем пятьсот тысяч нулей и на двух километрах один миллион. А так как нулей восемьдесят квадриллионов, или восемьдесят биллионов миллионов, то ленточка наша будет длиной в сто шестьдесят биллионов километров! Ленточка не маленькая: она в четыре с лишним раза длиннее орбиты, по которой несется планета Плутон. Свет, как ты знаешь, двигается довольно быстро. Однако все-таки, если бы на одном конце нашей ленточки мелькнула яркая звезда, на другом конце ее увидали бы не сразу, а только через шесть суток.

Но ведь это еще только изображение архимедова числа, а не само число!

- Удивительно! - сказал Илюша.

- Работы Архимеда были удивительны не только для тебя, но и для людей недюжинных способностей и великих знаний.

- 175 -

----------------

Первые архимедовы числа.

Единицы ...... 10°

Тысячи ...... 10³

Миллионы ..... 10⁶

----------------

10⁸ - вторые архимедовы числа (мириады мириад).

----------------

Биллионы ..... 10⁹

Триллионы ..... 10¹²

Квадриллионы .... 10¹⁵

----------------

10¹⁶ - третьи архимедовы числа.

----------------

Квинтильоны .... 10¹⁸ *

Секстильоны .... 10²¹

Септильоны .... 10²⁴

----------------

10²⁴ - четвертые архимедовы числа.

----------------

Октильоны .... 10²⁷

Нонильоны .... 10³⁰ **

Децильоны .... 10³³

----------------

10³² - пятые архимедовы числа.

----------------

Тысячи децильонов ..... 10³⁶

Миллионы децильонов .... 10³⁹

Биллионы децильонов .... 10⁴²

----------------

10⁴⁰ - шестые архимедовы числа.

----------------

Триллионы децильонов . . . 10⁴³

Квадрильоны децильонов . . 10⁴⁸

Квинтильоны децильонов , . 10⁵¹

----------------

10⁴⁸ - седьмые архимедовы числа.

----------------

Секстильоны децильонов . . 10⁵⁴

Септильоны децильонов . . . 10⁵⁷

Октильоны децильонов . . . 10⁶⁰ ***

----------------

10⁵⁶ - восьмые архимедовы числа.

----------------

Нонильоны децильонов . . . 10⁶³

Децильоны децильонов . , . 10⁶⁶

----------------

10⁶⁴ - девятые архимедовы числа.

----------------

* Здесь стоит число, равное сумме зерен пшеницы на шахматной доске в шестьдесят четыре клетки. Примерно оно равно 10¹⁹ • 1,8447.

** Здесь стоит число, равное сумме зерен на шахматной доске в сто клеток. Примерно оно равно 10³⁰ -1,2677.

*** Здесь стоит число, равное сумме зерен на шахматной доске в сто девяносто шесть клеток. Примерно оно равно 10⁵⁹ • 1,0039.

Древний историк Плутарх так говорил об Архимеде: "Во всей геометрии нет теорем более трудных и более глубоких, нежели теоремы Архимеда. Мне самому всегда казалось, когда я впервые знакомился с его математическими предложениями, что они до того трудны, что ум человеческий не в состоянии найти им доказательства. Однако когда узнаешь, как сам Архимед их доказывает, то тебе кажется, будто ты сам нашел это доказательство - до того оно просто и легко".

- 176 -

- Ты знаешь, я иногда сам что-то в этом роде чувствовал! .. Только не но отношению к Архимеду, а вообще по отношению к математике. Я очень хорошо понимаю, что хочет сказать этот древний историк!

- Так оно и должно быть, - с улыбкой ответил Радикс. - Ты испытываешь это светлое чувство радостного удивления перед могуществом человеческого разума, когда встречаешься с элементарными положениями, а люди, более тебя начитанные, испытывают то же, когда видят более сложные построения. Это вполне естественно. Один из самых крупных математиков семнадцатого века, Лейбниц, который очень много сделал для развития высшей математики, так сказал об Архимеде: "Когда внимательно разбираешься в творениях Архимеда, то постепенно перестаешь удивляться новейшим открытиям современных геометров". Два других великих математика - французы Лагранж и Даламбер - в восемнадцатом веке тоже немало потрудились над созданием высших разделов математики. Они писали об Архимеде: "Ни один из геометров древности не сделал таких многочисленных и важных открытий. Поэтому какими бы важными преимуществами ни обладали новые методы и как бы это ни было общеизвестно, тем не менее каждый математик должен поинтересоваться, какими тонкими и глубокими размышлениями Архимед сумел достигнуть таких сложных результатов". А замечательный английский математик Валлис, современник Ньютона, даже называл его "человеком сверхъестественной проницательности". Да и в гораздо более раннее время, когда ни Лейбница, ни Валлиса, ни Даламбера с Лагранжем не было еще на свете, крупнейшие ученые, которые впервые начали снова двигать вперед математику после долголетнего застоя, такие люди, как, например, Иоганн Кеплер (шестнадцатый-семнадцатый века), прямо говорили, что они пытаются продолжать дело Архимеда, а Бонавентура Кавальери (современник Кеплера и ученик Галилея) с гордостью утверждал, что ему удалось проникнуть в тайны того аналитического метода, которым Архимед пробивался через самые неприступные проблемы. Вот какой это был замечательный человек! Кавальери гордился тем, что сумел восстановить его методы. Мы еще поговорим с тобой об этом замечательном ученом. Ньютон однажды сказал, что он совершил свои открытия, так как "стоял на плечах гигантов". Кто же эти гиганты?

Это раньше всех Кеплер и Галилей.

- Да! - отвечал в почтительной задумчивости мальчик. - Только ведь это сочинение Архимеда о счете песка никаких особенных задач не решает. Правда?

- Ошибаешься! - отвечал Радикс. - Это сочинение имеет необыкновенно важное значение, и даже гораздо более важное, нежели решение какой-либо частной проблемы. Оно ставит такие серьезные вопросы, которых никто еще до Архимеда на практике не решался касаться; если же и касался, то, так сказать, несознательно, не представляя себе всей важности этой задачи. Она, в частности, заключается в доказательстве положения, утверждающего, что ум человеческий способен легко строить числа, превышающие любую заранее заданную величину.

- 177 -

Сам Архимед определял задачу этого сочинения так: оно должно доказать, что данное число песчинок не бесконечно и что возможно построить число, превышающее его. Но ведь песчинки - только частный пример, поэтому я настаиваю на моем первом определении задачи "Псаммита" (так называется по-гречески это сочинение Архимеда).

- Это очень интересно, - ответил Илюша поразмыслив. - Но ведь это только для того, чтобы посмотреть, к чему приведет такая странная задача? Не правда ли?

- Напрасно ты так думаешь, - ответил, нахмурясь, Радикс, - совершенно напрасно!.. "Псаммит" был сочинен Архимедом не для праздной забавы, отнюдь. Чем более серьезные задачи ставил перед собой человек в те древние времена (задачи из области физики, механики, астрономии и так далее), тем более сложный математический аппарат ему был нужен. И вот, чтобы начать строить этот аппарат, ему, человеку, и понадобились очень большие числа. Громадные! Необъятные! И "Псаммит" Архимеда был первым серьезным шагом в этой области. После того как содержание этого сочинения Архимеда было усвоено, можно было ставить себе и иные задачи. Например: что мы будем получать, если начнем последовательно делить единицу на ряд чисел Архимеда и дойдем до самых больших из названных им чисел?

- По-моему, - сказал Илюша, - это будет история путешествия синьориты Одной Энной по натуральному ряду.

- Недурно сказано! - воскликнул Радикс. - Недурно!

- По-видимому, эта особа будет все уменьшаться в объеме.

- А не найдешь ли ты такого числа, на которое она все более и более будет походить?

- Не знаю, - произнес мальчик осторожно, - какое же это может быть число. Ну, разве что нуль? То есть я хочу сказать, что чем дальше будет продолжаться прогулка синьориты Одной Энной по натуральному ряду, тем труднее ее будет отличить от нуля.

- Это разумный вывод, - отвечал одобрительно Радикс. - Так, конечно, и будет. Ну, а что случится, по-твоему, если я возьму все значения твоей приятельницы, госпожи Одной Энной, и начну теперь делить единицу на каждое из ее значений? Ну-ка!

- Ясно, - отвечал Илюша, - что ты снова получишь все те целые числа, с которых я начал, когда мы заговорили и синьорите Одной Энной.

- 178 -

- Прелестно! Рад от души!.. Но скажи на милость, а нет ли такой величины или даже такого математического образа, на который все более и более будут походить эти все растущие и растущие обратные величины значений синьориты Одной Энной?

Илюша не знал, что ответить на это, и только высказал предположение, что числа эти будут невообразимо громадны, так что вскоре даже и слава пресловутого "последнего" архимедова числа сильно потускнеет.

- Послушай, Илюша, - промолвил" Радикс, - ты только что сказал: что ни далее, тем значения синьориты Одной Энной все менее и менее будут отличаться от...

- От нуля.

- Правильно. Следовательно, перед нами будет ряд частных, делители которых все приближаются и приближаются к нулю. Прекрасно! А к чему же будут приближаться частные?

Илюша призадумался. Затем он сказал так:

- Видишь ли, я слышал, что есть такое слово "бесконечность". Только я не знаю: правильно ли будет, если мы сейчас о нем вспомним? Как ты скажешь?

- Это дело серьезное. И даже весьма. Тут есть над чем голову поломать. А в общем, чтобы подвести итог нашему разговору о "Псаммите", попробуй скажи мне в одной фразе, что там говорится.

Илюша подумал и ответил так:

- Какую бы мой собеседник величину ни назначил, я немедленно сооружу число во много раз больше.

И Радикс улыбнулся, на этот раз вполне удовлетворенный ответом Илюши.

- 179 -