Схолия Четырнадцатая,

Схолия Четырнадцатая,

посвященная самым возвышенным чудесам и до крайности загадочная, ибо хотя в ней снова толкуется о сырах, но сыры эти до такой степени замысловаты, что тех, кто их придумал, неоднократно и совершенно всерьез обзывали безумцами, а так как это делалось печатно, то отчасти напоминало ругань.

Речь идет всего лишь о том, как купить себе полчасика сыру, да кстати еще и о том, как поступил бы король Альфонс Кастильский, если бы он присутствовал при сотворении мира.

Затем вслед за таинственным появлением дивных древних теней мы видим одну забавную веревочку двухтысячелетней давности, одну особу весьма несложного устройства и аппарат, который понимает положительное и отрицательное совершенно по-своему и в особом смысле, хотя речь идет всего лишь о фисташковой скорлупе и самых обыкновенных кавалерийских седлах, а также о том, каким именно гигиенически-геометрическим телом надлежит пользоваться по утрам благонравным малюткам, и о некоем мире, где нет надобности в мерах длины.

Справедливость, однако, заставляет старательного автора этой правдивой книжки сообщить читателю еще следующее: дело в том, что - внимание! внимание! внимание! говорит ВОЛШЕБНЫЙ ДВУРОГ! - необыкновенные, неслыханные чудеса этой ослепительной схолии суть чудеса не простые, а особые.

- 254 -

А особенность их заключается в том, что их сразу трудно разглядеть, они сперва кажутся совершенно неуловимыми! По этой причине всякий из наших прилежных и усидчивых читателей, кто столкнется с этим странным явлением, должен поступить очень просто: прочесть эту трогательную схолию еще раз и еще раз, дабы наконец разобраться, как идут дела в том самом удивительном мире, где никогда ничего подобного не бывает!

Илюшины приятели и наставники так громко спорили друг с другом, с таким жаром доказывали, что врать не должно, но ставить в тупик в высшей степени похвально, что Илюше стало скучно, и он потихоньку выбрался из домика Асимптотоса. Пахучий воздух, красивые купы вечнозеленых растений и тишина словно обступили его со всех сторон. Неподалеку снова раздались знакомые звуки флейты, и козлоногий Фавн выскочил из-за кустов. Наконец он опустил свои флейточки и оглянулся на домик Асимптотоса, откуда в то время донесся крик доктора У. У. Уникурсальяна: "А я, напротив того, буду утверждать, что то, что не невозможно, тем самым и является основным и даже единственным прототипом общеобязательного!.." Фавн поманил Илюшу немного подальше и, нагнувшись к самому его уху, торопливо начал шептать:

- У них еще есть! Что есть - боюсь сказать. Но то же... вроде... Тесс! Молчок! Дело в том, что у них, видишь ли, есть еще... особые сорта голландского. Один называется альмагестическим сыром. Это давнишний сыр, традиционный, легендарный, многозвездный, покровитель мореходов, любимый сыр звездочетов, пока, разумеется, они еще не знали того, шотландского сыра. А сверх того еще один сыр, необыкновенный, якобы круглый... Называется - казанский.

- Казанский? - переспросил Илюша с удивлением.

- В этом городе сварили такой сыр, что самые серьезные люди называли этого дивного сыровара Коперником геометрии!

Это был второй Евклид. И представь себе, что эти сыры измеряют не на килограммы, потому что это и устарелый и неостроумный способ. На километры тоже неудобно - очень длинно! Долго они думали над этим вопросом. Пробовали мерить мегомами, атмосферами, люксами, кулонами, лошадиными силами, грамм-молекулами, большими калориями - и все как-то не получалось.

Но когда Коникос умножил одну секунду на шестьдесят в квадрате, то вышло в самый раз.

- Шестьдесят в квадрате секунд? - сказал Илюша. - Да это ведь час? Как же это так? Приходишь в магазин и говоришь: "Будьте так добры, дайте-ка мне полчасика сырку!"

- 255 -

- Ну почему час? - возразил козлоногий его собеседник. - Не час, а градус! Даже и градус-то не особенно удобная мера для сыров. Они меряют сыр, умножая градус еще на девяносто, то есть, попросту сказать, меряют его прямыми углами.

Когда ты попросишь: "Отпустите мне альмагестического сыру три прямых", тут уже все ясно и никаких недоразумений быть не может.

Илюша никак не мог сообразить, как это можно измерять сыр прямыми углами, однако он заинтересовался этим, потому что только что убедился, что все, что в прошлой схолии ему рассказывали о различных сырах Фавн, Дриада и громкоговоритель, хотя на первый взгляд это и была чушь непролазная, в дальнейшем получило вполне понятное объяснение.

Поэтому он и сейчас подумал, что, наверно, Фавн, рассказывая ему об альмагестическом и казанском сырах и отвешивании оных при помощи прямых углов, имеет в виду что-то необыкновенно интересное. В это время занавесь домика Асимптотоса широко распахнулась, оттуда выскочил покрасневший, как свекла, Коникос и крикнул:

- Молодой человек! Куда ты девался?

Илюша, недовольный тем, что его оторвали от такого интересного разговора, вышел потихоньку из-за кустов. А из домика показался очень взволнованный Асимптотос.

- Справедливые боги! - воскликнул он, воздевая руки ввысь. - Вот благодарность за мои красноречивые рассказы!

Убежать от меня в лес и там начать болтовню с какой-то бессловесной скотиной! Клянусь плавающим параболоидом Архимеда, ведь ты же неведомо чего от него можешь набраться!

Идем скорей!

- Я не знал, - сказал смущенный Илюша. - Но у вас там такой крик стоял...

- Не крик, а чисто принципиальное недоумение! - строго ответил ему Магистр Деревьев, высунувшись из-за занавеси.

Илюша не осмелился вступать с ними в пререкания и снова вошел в домик.

Стоявший в уголке Радикс досадливо погрозил ему пальцем. Илюша поспешно подошел к нему.

- Послушай, Радикс, - сказал он еле слышным шепотом, - я просто вышел на минутку. А этот Фавн, тот самый - помнишь?..

Но не успел Илюша докончить этой фразы, как около него словно из-под земли вырос всепроницающий Командор О. С. М.

- Это что такое? - строго вопросил он. - Кто это тебе позволил, гадкий мальчик?

- 256 -

А не хочешь ли, я прикоснусь к тебе при помощи касательной так, что ты у меня улетишь на такую бесконечно удаленную точку, что тебе оттуда архимедово число с квадриллионами нулей с единичку покажется?

И не успел еще Илюша рта раскрыть, как Доктор Четных и Нечетных воскликнул гневно, мрачно и торжественно:

- Молчание!

И вдруг лопнул, рассыпавшись разноцветными искрами.

Радикс, Асимптотос и Коникос стояли озадаченные, оторопевшие.

- Н-н-ну-с... - произнес слегка вздрагивающим голосом Коникос, - кажется, обошлось... Но, пожалуйста, не шали больше! Приступим к дальнейшему.

И в тот же миг перед нашими друзьями вырос громадный шар, метров трех в диаметре. Коникос снова взял в руки свой широченный нож, подошел к громадному шару и начал:

- Если взять поверхность обыкновенного шара, то есть сферу, то из нее возможно получить некоторый своеобразный треугольник.

Тут Коникос разрезал сферу своим широченным ножом ровно пополам, по экватору, и толкнул нижнюю половинку; она сдвинулась, откатилась и исчезла, а верхняя половина медленно опустилась на пол. Коникос снова разрезал ее пополам. А затем получившуюся четвертинку сферы он рассек еще раз надвое.

- Ну, вот-с! - сказал он, поглядывая на эту восьмую часть сферы. - Я утверждаю, что я получил треугольник. И я попрошу тебя, Илюша, выяснить, чему равняется сумма его углов.

- Мне кажется, - отвечал Илюша, - что вот этот угол, который поближе, очень похож на прямой... Но только я не уверен, что его можно называть прямым, просто потому, что не знаю, как измеряется угол между двумя кривыми.

- Измеряется он довольно просто, - отвечал Коникос. - Мы в таком случае меряем угол не между самыми кривыми, а между двумя их касательными, касающимися наших кривых как раз в той точке, которая есть вершина нашего угла. Ясно?

- Да, как будто ясно, - отвечал мальчик.

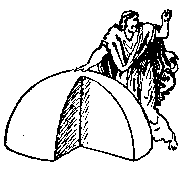
Илюша внимательно осмотрел получившийся у Коникоса кусок сферы, но сперва не обнаружил во всем этом ничего интересного. Разрезали шар на восемь частей - что же тут особенного? Иной раз так и арбузы режут...

- 257 -

- Я думаю, - заявил Илюша приглядевшись, - что этот кусок сферы образует с плоскостью, на которой он лежит, только прямые углы. Угол А прямой (смотри на картинку!), угол В прямой, и угол С тоже прямой! Следовательно, поверхность шара- сфера, - разрезанная таким образом, дает треугольник, сумма углов которого равняется трем прямым углам. Но как же это может быть? Ведь в настоящем треугольнике сумма углов равна двум прямым углам!.. Впрочем, это треугольник кривой, а если его растянуть на плоскости...

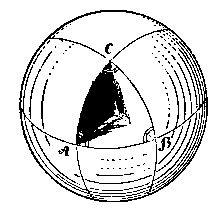
- А ну попробуй растяни! - сказал Асимптотос, приподняв свой треугольник и подавая его Илюше. - Только не рвать!

Илюша начал растягивать, но оказалось, что этот странный треугольник не хочет растягиваться. Когда Илюша нажал на него покрепче, он выгнулся в другую сторону, как зонтик под сильным ветром, но растягиваться не соглашался.

- Вот как, Илюша! - сказал Радикс. - Учил ты, учил планиметрию, а как до трех прямых дошло, так и запутался!

Ты прими во внимание: все, что ты учил о треугольниках, правильно, пока они на плоскости. И там все евклидовы теоремы правильны. Так и говорится: "евклидова геометрия".

А на шаре мы получаем не-евклидову геометрию. Если взять огромный шар и рассматривать маленькие треугольники, то чем шар больше, тем ближе их геометрия приближалась бы к евклидовой. Если бы радиус шара был безгранично велик, тогда бы и на его поверхности Евклид оказался прав. А на данной сфере в таком треугольнике сумма углов зависит от его площади, тогда как на плоскости это величина постоянная и равна 2d. А это сферический треугольник, но не плоский.

- И существует, - добавил Коникос, - особая сферическая тригонометрия, которая весьма необходима мореплавателям и астрономам. Она даже появилась на свет ранее обычной в одном астрономическом сочинении Клавдия Птолемея, так называемом "Альмагесте", написанном около сто тридцатого года вашей эры в Александрии.

"Так, так, так! - подумал Илюша. - Вот почему Фавн говорил об альмагестическом сыре и прямых углах!"

- До Коперника, - продолжал Коникос, - это было самое серьезное и самое авторитетное сочинение по астрономии.

- 258 -

Европейцы узнали его в арабском переводе, и под этим арабским названием "Альмагест" оно и стало известно. Именно там и изложена геоцентрическая теория Птолемея. Настоящее заглавие этого сочинения - "Великое построение математическое". Оно несомненно заслуживает такого названия, ибо долгое время служило на пользу людям.

- Но ведь это же было неверно, - сказал Илюша, - раз он считал, что в центре нашей системы находится Земля, а не Солнце? Мне вспоминается, что у Ломоносова есть даже стихи по этому поводу...

- Какие такие стихи? - спросил Гадикс.

- Постой-ка, сейчас вспомню, - отвечал мальчик. - Ага... вот как:

Случились вместе два астронома в пиру

И спорили весьма между собой в жару.

Один твердил: Земля, вертясь, круг Солнца ходит;

Другой - что Солнце все с собой планеты водит.

Один Коперник был, другой слыл Птолемей.

Тут повар спор решил усмешкою своей.

Хозяин спрашивал: "Ты звезд теченье знаешь?

Скажи, как ты о сем сомненье рассуждаешь?"

Он дал такой ответ: "Что в том Коперник прав,

Я правду докажу, на Солнце не бывав.

Кто видел простака из поваров такого,

Который бы вертел очаг кругом жаркого!"

- Возможно, это и так, - отвечал Асимптотос, - в том смысле, что с физической точки зрения естественней считать центром системы Солнце, а все-таки службу "Альмагест" сослужил немалую. И без него было бы не так-то просто построить современную систему. Но система "Альмагеста" уже тем нехороша, что она чересчур сложна. Планета двигалась у Птолемея вокруг Земли не просто по кругу, а по некоторому небольшому кругу, а центр этого круга, в свою очередь, катился по другому, большому кругу, в центре которого находилась Земля. Круги вертелись в разные стороны, да еще с переменной скоростью. Если составить карту звездного неба и нарисовать на ней путь движения какой-нибудь планеты на фоне неподвижных звезд ("планета" ведь и значит "блуждающая звезда"), то окажется, что он представляет собой кривую, которая образует петли. Планета двигается в определенном направлении, затем начинает опускаться, потом как бы идет назад, в "обратном направлении", снова поворачивает и, описав таким образом петлю, вновь начинает двигаться в том же примерно направлении, с которого мы начали.

- 259 -

- Можно сказать еще, - добавил Коникос, - что греческим ученым казалось, что все планетные движения можно объяснить равномерными движениями по кругам. Но это не удавалось. Поэтому и была создана система Птолемея, то есть сложная система кругов (так называемых эпициклов и деферентов), которая имела в виду воссоздать теоретически эти петли планетных движений, что ей и удалось. Это придумал Аполлоний Пергейский, наш великий покровитель. Однако даже и эта сложная система не всегда давала правильные решения при отыскании места планеты на небе в тот или иной момент, и приходилось иногда вводить еще и третий круг. Рассказывают, что король Кастилии Альфонс Мудрый (XIII век нашей эры), твердо веривший, что еврейский бог некогда из ничего "сотворил" мир в шесть дней, ознакомившись с системой Птолемея, воскликнул: "Если бы я присутствовал при сотворении мира, я бы посоветовал господу богу устроить его как-нибудь попроще!" Александрийские астрономы, впрочем, не задавались целью определить, как двигаются планеты в трехмерном пространстве. Эта мысль пришла людям в голову много позже. Александрийцы были довольны и тем, что с календарем у них на небесном своде выходит все правильно. Коперник, однако, подошел ко всей задаче с точки зрения пространственной. И тогда ему не так уж было трудно объяснить, что на самом деле планета никаких Птолемеевых петель не описывает, а мы их видим потому, что смотрим на планету из различных точек в мировом пространстве. Если же смотреть на планету не с Земли, а с Солнца, то никаких петель мы не заметим.

- Понял? - спросил Радикс.

- Не-не... очень... - признался Илюша.

- 260 -

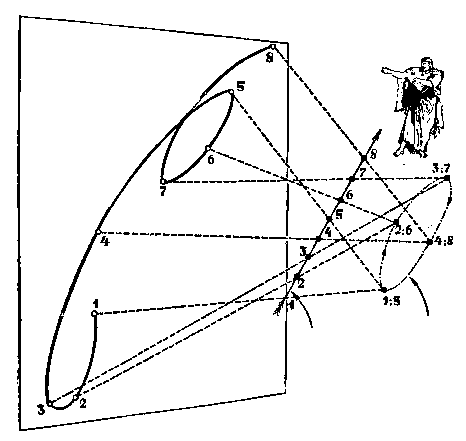
- А мы сейчас тебе расскажем. Ты смотришь с Земли на Солнце и на планету. Солнце за год обойдет окружность вокруг тебя, - тут все просто. Но ведь планета ходит не вокруг тебя, а вокруг Солнца. Следовательно, когда ты смотришь с Земли, ты видишь, как планета, двигаясь вокруг Солнца, вместе с ним двигается вокруг тебя. И выходит, что она совершает вокруг тебя нечто вроде винтовой линии. Ты смотришь на нее сбоку - вот и получаются петли. Ну как? Дошло?

- Как будто дошло, - отвечал Илюша. - Но ведь мы считаем, что не Солнце ходит вокруг Земли, а Земля вокруг Солнца...

- Чтобы понять, что ты будешь "видеть", нет нужды становиться на эту "точку зрения".

- Ведь дело-то не так уж хитро, - добавил Коникос, - если исходить из движения Земли по орбите. И все это легко выяснить на опыте.

- 261 -

Он махнул рукой, и в домике стало темно. Перед стеноп повис в воздухе небольшой еле светящийся шарик, а в руке у Коникоса оказался другой, испускавший довольно яркий свет, так что слабо светящийся шарик отбрасывал тень на стену.

- Допусти, - сказал Коникос, - что я наблюдаю с Земли за этим светящимся шариком, который есть не что иное, как планета. А стена у нас будет тем самым фоном неподвижных звезд, который виден с Земли и по которому мы и судим о движении планеты.

Коникос поднял свой ярко светящийся шарик и пошел справа от Илюши, затем назад к нему, а потом снова от него и снова к нему, изображая движение Земли по орбите. Тень слабо светящегося шарика, висевшего в воздухе, ровно ходила по стене туда и сюда как раз в противоположную сторону тому, куда двигался Коникос.

- Я, - сказал Коникос, - двигаюсь в пространстве, а планета моя не двигается. Ты видишь, что делается с тенью ее?

- Вижу, - отвечал Илюша.

- Теперь пусть наш слабо светящийся шарик идет вперед, параллельно стене.

Слабо светящийся шарик двинулся медленно вперед, а Коникос по-прежнему продолжал ходить из стороны в сторону.

Теперь тень светящейся точки сперва пошла назад, потом повернула и бросилась вперед, но спустя некоторое время снова повернула назад, а потом опять бросилась вперед.

- Ну, теперь я понял, - сказал Илюша.

- Надо еще не забывать о том, - добавил Радикс, - что наука о звездном небе с самых древних времен была необходима человеку в его путешествиях. Мореход в открытом море определяет свое положение по звездам. Так же поступает и кочевник в пустыне, где тоже нет ориентиров. Знания о звездах накапливаются и постепенно превращаются в науку. Наш русский путешественник-естествоиспытатель В. К. Арсеньев рассказывает[18], как зимой в тундре, среди необозримых снегов он кочевал с одним племенем тунгусов. Однажды ему сказали, что дня через два они сойдутся с другим кочующим народом. Наконец кочевники выбрали себе какое-то место, которое, по мнению Арсеньева, ничем не отличалось от других.

К вечеру старики стали наблюдать небо, но жаловались, что густая облачность не дает рассмотреть то, что им надо, и из-за этого они не совсем уверены, так ли выбрали место стоянки, ибо их родичи придут на определенное место. Прошло два дня, и утром, проснувшись, Арсеньев с изумлением обнаружил, что другие кочевники пришли на то же место. A в дальнейшем ему неохотно и не очень толково объяснили, что старики определили место по звездам, причем очевидно, что старики в обеих группах кочевников руководствовались одними и теми же признаками. Значит, астрономии человека учила сама жизненная необходимость!

- 262 -

- Ну теперь, - сказал Асимптотос, - вернемся еще к нашему сферическому треугольнику. Лучше сказать - к геометрии на сфере. Выясним, какие линии играют на сферической поверхности роль прямых. Архимед в сочинении "О шаре и цилиндре" вводит допущение, что прямая есть кратчайшее расстояние между двумя точками, откуда мы приходим к заключению, что "прямой" на сфере будет дуга большого круга, то есть такого круга, который получится при сечении сферы плоскостью, проходящей через центр сферы. Если это так, то очевидно, что на сфере не может быть параллельных "прямых", ибо две "прямые" обязательно пересекаются в. двух точках (как меридианы на полюсах). Площадь треугольника на сфере тем больше, чем более превышает сумма его углов плоскостную меру, то есть два прямых угла. Что касается до "прямых" на сфере, то это очень просто можно проверить на глобусе при помощи резиновой нитки. Попробуй-ка на глобусе поехать по тридцать девятой параллели из Лиссабона в Нью-Йорк или из Иокогамы в Сан-Франциско.

- Обязательно попробую! - сказал Илюша.

- И хорошо сделаешь, - отвечал Радикс. - Знай, что это обстоятельство крайне затрудняет черчение географических карт на плоскости и что над разрешением вопроса о том, как начертить карту, чтобы искажение масштабов было наименьшим, работал крупнейший русский математик Пафнутий Львович Чебышев, живший в девятнадцатом веке, а также и ученики его. Я тебя вот еще о чем спрошу: если мы начертим какую-нибудь геометрическую фигуру на плоском листе бумаги, а потом изогнем этот кусок бумаги как-нибудь, то что сделается с теми линиями, которые у нас на плоскости были прямыми?

- Они уже не будут прямыми, - отвечал Илюша.

- Правильно, - согласился Коникос. - Но кратчайшими расстояниями среди линий, соединяющих две точки на поверхности и целиком лежащих на поверхности, они останутся. Такие линии называются геодезическими. Геодезическими на сфере, очевидно, являются большие круги.

- Самое интересное, - добавил Радикс, - это то, что на сфере совсем не может быть параллельных линий.

- 263 -

- Н-да, разумеется... - задумчиво и неопределенно протянул Асимптотос. - Однако ведь у нас есть еще один необычайнейший треугольник. Сумма его углов не больше 2d и не равна 2d, а меньше двух прямых углов.

- Это уж что-то совсем непонятное! - сокрушенно заявил Илюша.

- Разумеется, - промолвил Радикс, - геометрия, в которой можно построить такой треугольник, есть тоже не-евклидова геометрия. Ее открыл и разработал великий русский геометр Николай Иванович Лобачевский, профессор Казанского университета. Он жил с тысяча семьсот девяносто третьего года по тысяча восемьсот пятьдесят шестой год. Его труды, опубликованные в тридцатых годах девятнадцатого столетия, были настолько поразительны и вели к таким необычным и неожиданным последствиям, что лишь немногие его современники могли понять и оценить эти труды.

- Надо тебе сказать, - продолжал вслед за другом Коникос, - что теорему Евклида, которая гласит, что сумма углов плоского треугольника равна двум прямым, можно вывести на основании одного из двух положений:

1) из одной точки можно провести только одну параллельную линию к данной линии или 2) всегда можно построить фигуру, подобную данной, но больше ее.

Таким образом, все эти положения тесно связаны друг с другом, так что если справедливо одно из них, то оправдываются и два других.

- Как это? - спросил Илюша.

- Слушай дальше: положение, или постулат, о параллельных принимается у Евклида за аксиому, однако, так как оно не кажется столь же очевидным и столь же простым, как другие аксиомы Евклида, то на протяжении долгих веков не прекращались попытки доказать этот постулат так, как доказывают теорему. Между прочим, одна из этих попыток - разумеется, не более удачная, чем все остальные - принадлежит автору "Альмагеста", Птолемею, который был незаурядным математиком. Однако теперь мы знаем, что большинство этих попыток свелось к тому, что допущение Евклида о параллельных бессознательно заменялось либо допущением о возможности построить подобную фигуру, либо допущением о том, что сумма углов треугольника есть величина постоянная и равна двум прямым. Существует, правда, кроме этих, еще несколько равнозначных положений, но их уж я касаться не буду. Наконец, все эти работы повели к тому, что геометры заметили (после работ Лобачевского) связь этих положений друг с другом и убедились, что "доказать" этот постулат Евклида невозможно. Однако этот постулат - или одно из перечисленных мной допущений - является необходимым, без него нельзя построить евклидову геометрию.

- 264 -

До Лобачевского очень многие полагали, что никакой другой геометрии, кроме евклидовой, не только нет, но и не может существовать. Мнение это было общепринятым. Иные утверждали, что евклидова геометрия есть наша "естественная" геометрия, которую человек всасывает чуть ли не с молоком матери. Но крупнейший немецкий математик Карл Гаусс на это возразил: "Мы не имеем права путать то, что нам кажется странным, с тем, что и на самом деле невозможно". Лобачевского на его труды натолкнули такие соображения: чтобы убедиться в том, что нет возможности доказать постулат Евклида о параллельных, следует попробовать построить геометрию, где бы этот важный постулат был вообще отброшен. Ход размышлений Лобачевского ты легко можешь усвоить, вспомнив, как доказываются геометрические теоремы "от противного". Мы, вместо того чтобы искать прямое доказательство, делаем противное допущение, и тогда, если в конце наших рассуждений мы сталкиваемся с противоречием, это опровергает наше противное допущение, тем самым подтверждая и доказывая то прямое положение, доказать которое нам и было нужно. Если постулат о параллельных необходим, то (так рассуждал наш великий геометр), мы, отбросив его, не сможем получить строгой системы геометрии и неминуемо придем к логическим противоречиям.

И таким образом мы проверим и необходимость и справедливость пятого (таков его порядковый номер в "Началах" Евклида) постулата. И вот Лобачевский строит новую геометрию,"воображаемую" геометрию, как он сам ее называл, где вместо постулата Евклида вводится иной, утверждающий, что из одной точки можно провести не одну, а две параллельные линии к данной.

Наконец он получает результаты своего изумительного прилежания и труда, и решение этой задачи пятого постулата. Но решение это оказалось таким, которого не ожидал и к которому не был готов почти никто из современных математиков, не говоря уже о философах, а еще менее о людях, не имевших специальных математических или философских знаний. Первое, к чему пришел Лобачевский, было утверждение, что пятый постулат никоим образом из всех иных положений геометрии выведен быть не может, а следовательно, его невозможно доказать как теорему, опираясь на иные, ранее доказанные положения или допущения.

Однако гораздо более важным оказалось то, что Лобачевский, развив свою новую геометрию до тех же пределов, до которых развил свою геометрию Евклид, нигде ни с какими противоречиями не встретился. Дальнейшие работы очень крупных математиков в конце прошлого века раскрыли этот вопрос до конца и полностью подтвердили выводы Лобачевского. А важнейший вывод "воображаемой" геометрии гласит следующее: потому-то и невозможно доказать пятый постулат Евклида, что наряду с евклидовой геометрией может существовать иная, где этот постулат не имеет силы!

- 265 -

- Ну, а как же люди примирились с этой странной геометрией, которая сначала всем не нравилась?

- Сперва, - отвечал Радикс, - работы Лобачевского не только не нашли признания, но даже были встречены насмешками. Гаусс писал об одном из таких отзывов своему другу Герлингу (в 1844 году), что он видел "весьма отрицательный" отзыв о работе Лобачевского, но по словам Гаусса, для каждого сколько-нибудь осведомленного читателя ясно, что писал это "совершенно невежественный человек". Гаусс сам работал над этой темой, но не решился опубликовать свои результаты именно из-за страха перед неосведомленной критикой... Однако нашлись математики, которые дали себе труд подумать и разобраться в "воображаемой" геометрии. Одним из таких людей был итальянский математик Бельтрами, который в конце шестидесятых годов прошлого века выпустил в свет сочинение, где дал такое наглядное истолкование не-евклидовой геометрии Лобачевского, что всем стало ясно, что эти построения действительно представляют собой геометрическую систему, в известном смысле равноправную с обычной, а не только "воображаемую" геометрию. Бельтрами показал, что в обычном трехмерном евклидовом пространстве можно построить такое тело, на частях поверхности которого будет осуществляться планиметрия Лобачевского, откуда ясно, что геометрия его не может заключать в себе внутренних противоречий.

- Как же так? - с удивлением спросил Илюша. - или это вроде этих сферических треугольников, не похожих на наши обыкновенные, плоскостные?

- Да, это в некотором смысле то же самое. На сфере тоже осуществляется не-евклидова геометрия, но это будет геометрия Римана, для которой, в отличие от геометрии Лобачевского, сумма углов треугольника больше двух прямых, а кроме того, там прямая линия безгранична, но не бесконечна...

- Что это значит? - спросил Илюша.

- Припомни, что такое экватор на глобусе. Ведь он границы не имеет, но он и не бесконечен. Не правда ли?

- Ах да, совершенно верно! - спохватился Илюша.

- Итак, - продолжал Радикс, - Бельтрами нашел такую поверхность, на которой "воображаемая" геометрия Лобачевского, по крайней мере в части планиметрической, осуществлялась, хотя и не совсем полностью. Эта поверхность напоминает стеклянную воронку и называется псевдосферой, или, если сказать более по-русски, это будет якобы сфера.

- 266 -

Ее можно легко построить, и мы ее сейчас тебе покажем при помощи нашей Центрифуги. Таким образом Бельтрами, а за ним и многие другие ученые доказали, что "воображаемая" геометрия занимается вещами вполне реальными. Изучение и развитие неевклидовых геометрий оказало нашей науке громадные услуги, о которых ты, если будешь учиться дальше, узнаешь очень много. А если коснуться просто повседневной жизни, то и тут стоит сказать: то, что люди называли "естественной" геометрией, - это просто геометрия на плоскости. А когда землемер меряет поверхность горы или оврага, когда портниха шьет платье, то им нередко приходится иметь дело с "неестественными" геометриями, ибо оба они встречаются с седлообразными поверхностями, напоминающими ту же псевдосферу. Недаром замечательный русский математик Пафнутий Львович Чебышев занимался портняжьей проблемой кройки платьев и сделал в тысяча восемьсот семьдесят восьмом году доклад на эту тему в одном французском ученом обществе и даже представил при этом собравшимся его слушать ученым мяч, обтянутый двумя кусками материи в некотором, совершенно точном, смысле слова "наилучшим" образом.

- Вот странно! - воскликнул Илья, - вот уж я никогда бы не подумал, что землемер или портниха занимаются не-евклидовой геометрией! Впрочем... я и о фонтанах китов тоже не догадался бы.

- Вот то-то и оно! - сердито возразил Радикс. - Имей в виду, кстати, что сам Бельтрами был геодезист, то есть именно землемер. Есть основания думать даже, что и великий Гаусс, который много занимался задачами практического землемерия, натолкнулся на неевклидову геометрию Лобачевского, именно размышляя о своеобразии геодезических задач. Кстати тебе сказать, все споры О "воображаемой" геометрии только тогда и закончились, когда была опубликована наконец переписка Гаусса, где он откровенно говорит своим друзьям о своих открытиях в области геометрии Лобачевского. Это случилось уже в шестидесятых годах прошлого века, а работы Лобачевского начались с двадцатых годов.

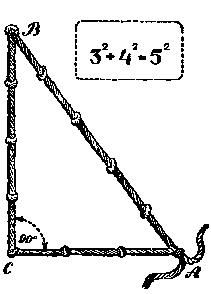
Египетский мерный шнур для построения прямого угла. В точках В и С вбиваются колышки. Получается прямой угол в точке с при одновременном натяжении ВА и СА.

- 267 -

Илюша посмотрел на Радикса и подумал: "Псевдосфера!

Вот почему Фавн говорил о псевдокруглом сыре. Понятно".

- Ну, а теперь, - сказал, усмехаясь, Асимптотос, - надо нам вспомнить еще Илюшиного друга - Пифагора.

- Кстати, - подхватил Коникос, - слышал ли ты легенду о "египетском мерном шнуре" с двенадцатью узлами? Греки даже называли египетских землемеров "арпедонапты", то есть "вервиетягатели".

- Нет, - отвечал мальчик.

- Двенадцать, - продолжал Асимптотос, - легко разбить на три слагаемых: три, четыре и пять...

- Пифагоровы числа! - воскликнул Илюша.

- Они самые! Вот поэтому-то при помощи шнура с двенадцатью узлами очень легко построить прямой угол, который нужен и землемеру и строителю. Египтяне знали это правило чуть не за три тысячи лет до вашей эры. У нас здесь есть тоже треугольник - некий волшебно-математический аппарат, который показывает, куда мы попали - в знакомую страну или в незнакомую, где евклидовы и пифагоровы правила не годятся.

- Я как будто догадываюсь. Этот аппарат проверяет, плоская эта поверхность или нет?

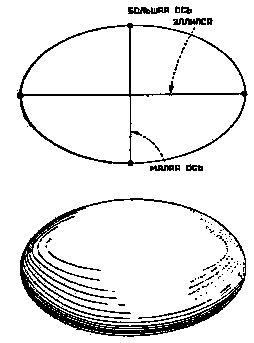
Эллипсоид вращения

- Он не только это проверяет, он еще указывает, далеко ли отклоняется от плоскости данная поверхность и как именно она это делает. А стоит тебе это узнать, и ты сейчас же сообразишь, какая там геометрия годится. Вот и все.

- 268 -

Илюша осмотрел аппарат, который представлял собой прямоугольный треугольник, сделанный из оловянного листа, а сбоку был циферблат со стрелкой. В середине стояла большая буква "Е", и на нее указывала стрелка. С одной стороны было написано "Положительная кривизна", а с другой - "Отрицательная кривизна".

Однополостный гиперболоид вращения

Когда Илюша приложил аппаратик к сфере, тот немедленно ответил: "Положительная кривизна". Когда же он приложил аппаратик к стене, то стрелка осталась стоять против буквы "Е", а буква "Е", конечно, напомнила об Евклиде.

- А это что значит? - спросил Илюша. - Ты, Радикс, ведь говорил, что если взять очень большой шар, то там геометрия будет почти такая же, как евклидова.

Значит, чем меньше я буду брать шар, тем будет "более кривая" поверхность с точки зрения этого аппаратика?

- Правильно! - отвечал Радикс. - Если, например, ты на поверхности земного шара будешь брать треугольник со сторонами менее ста километров, ты можешь смело считать его совершенно плоским.

- Ну, а что может значить "отрицательная" кривизна?

Асимптотос с сомнением покачал головой и принес две кривые: одна была эллипсом, другая гиперболой.

- Наша Центрифуга есть поистине дивный аппарат для получения поверхностей вращения.

Затем он взял эллипс и прикрепил его вдоль и посредине (то есть по его большой оси - смотри на картинке!) к стержню, пустил в ход Центрифугу, а потом сиял получившееся тело со стержня.

- Это эллипсоид вращения, - объяснил он.

Однополостный гиперболоид вращения.

- 269 -

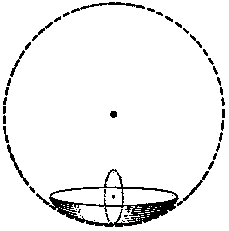
Центры кругов кривизны находятся по одну сторону поверхности - положительная кривизна.

Тут он взял две ветви гиперболы и повесил их симметрично в воздухе на равных расстояниях от стержня.

- Простите, пожалуйста! - взмолился Илюша. - Вот когда вы снимаете с Центрифуги конус или эллипсоид, которые, собственно, состоят из ничего, и ставите на пол, ведь это волшебство?

- Мы все друзья и слуги ВОЛШЕБНОГО ДВУРОГА! - отвечал Асимптотос, торжественно подняв ввысь палец.

- А когда вы вешаете эти кривые в воздухе, это тоже волшебство?

- Не совсем! Я прикрепляю гиперболу к стержню при помощи со мнимой оси. Ну, а так как она мнимая, то ее, разумеется, довольно плохо видно. Вот и все! Если мы рассекаем два конуса с общей вершиной, мы получаем две ветви гиперболы.

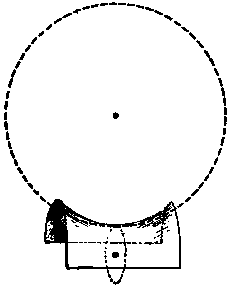
Центры кругов кривизны находятся с разных сторон поверхности - отрицательная кривизна.

Они симметричны в двух направлениях. Во-первых, они симметричны относительно действительной, или вещественной, оси гиперболы, параллельной оси нашего конуса. А во-вторых, они симметричны относительно воображаемой линии, перпендикулярной к оси конуса. Эта линия называется мнимой осью гиперболы. Вот я ее и надел на стержень.

- 270 -

Затем Асимптотос пустил в ход быстролетную Центрифугу. Вскоре из двух ветвей гиперболы образовалась поверхность вращения, средняя часть которой представляла собой кольцо с загибающимися краями.

- Это однополостный гиперболоид вращения.

Трехосный эллипсоид.

Если бы мы вращали гиперболу по вещественной оси, мы получили бы двуполостный гиперболоид, то есть две отдельные чаши. Ну, теперь все.

Он поставил гиперболоид на пол рядом с эллипсоидом.

- Начнем с эллипсоида. Замечаешь ли ты, что в длину он согнут не так, как в ширину? Ясно, что и в ширину он в сечении даст круг, но дело в том, что в длину, то есть по своей большой оси, если мы будем рассматривать точку над самой ее серединой, он гнется не так сильно, как гнется в том же месте по направлению малой оси.

- Конечно! - отвечал Илюша.

- Следовательно, в одном направлении у него одна кривизна, в другом - другая. Теперь я разрежу эллипсоид пополам и возьму два круга - один побольше, другой поменьше.

Асимптотос разрезал эллипсоид вдоль. Оказалось, что он внутри совершенно пустой. Получилось такое эллиптическое корытце, вроде половинки скорлупы фисташкового ореха, если бы, конечно, орех был в точности симметричен.

- Смотри! - сказал Коникос. - Маленький круг я могу в него вставить и по направлению малой оси и по направлению большой. Маленький круг совпадает с сечением эллипсоида по малой оси и измеряет его кривизну в этом направлении.

А большой круг по малой оси в это эллиптическое корытце не влезает, но зато он очень хорошо входит в корытце по большой оси. Конечно, круг не совпадает с сечением по большой оси, ибо это сечение есть эллипс, а не круг, но он соприкасается с этим сечением как только возможно тесно. Этот круг измеряет кривизну эллипсоида по большой оси, однако только в данной точке. Ясно, что круги становятся друг к другу перпендикулярно, потому что ведь и сами оси перпендикулярны.

Самое важное в этом случае то, что центры обоих кругов находятся с одной и той же вогнутой стороны эллипсоида. Понял? Вот когда центры кругов, измеряющих кривизну, оказываются с одной стороны поверхности, то такая кривизна называется положительной.

- 271 -

Откуда идут эти названия, сразу не расскажешь, и на этих тонкостях я останавливаться не буду. А теперь перейдем к гиперболоиду.

Асимптотос разрезал и гиперболоид вдоль.

Получились две седлообразные поверхности, похожие на горный перевал.

- Смотри внимательно! - сказал Асимптотос. - Я беру снова среднюю точку и буду измерять кривизну опять теми же кругами и по таким же Двум взаимно перпендикулярным осям.

Когда Асимптотос начал приставлять круги к этой седлообразной поверхности, то оказалось, что эта поверхность в продольном направлении вогнутая, а в поперечном - выпуклая.

Поэтому центр большого круга оказался вне гиперболоида, а центр маленького - по другую сторону поверхности гиперболоида. Центры кругов оказались с разных сторон поверхности.

- Ну вот! - сказал Асимптотос. - Когда центры кругов кривизны оказываются с разных сторон поверхности, то это и называется отрицательной кривизной. Геометрия Лобачевского осуществима только на поверхности с отрицательной кривизной. Однако слушай далее внимательно, ибо это еще не все.

Сфера имеет во всех своих точках одну и ту же кривизну. Мы говорим, что эта поверхность постоянной положительной кривизны. Ясно, что хотя эллипсоид имеет тоже положительную кривизну, но она отнюдь не постоянна. Однополостный гиперболоид, наоборот, имеет отрицательную, но тоже непостоянную кривизну. Спрашивается: имеются ли поверхности постоянной отрицательной кривизны? Такие поверхности были открыты еще до Бельтрами. Отличительной особенностью поверхностей постоянной кривизны является то, что кусок такой поверхности может скользить по ней самой без разрывов и сжатий, как футляр шара по поверхности шара или кусочек бумаги по гладкой поверхности стола либо цилиндрической колонны. Важнейшее открытие Бельтрами состояло вот в чем: он обнаружил, что треугольники, сторонами которых являются кратчайшие линии на поверхности постоянной отрицательной кривизны, подчиняются "воображаемой" геометрии Лобачевского. Таким образом, выяснилось, что плоская геометрия Лобачевского осуществляется на одной из простейших поверхностей с постоянной отрицательной кривизной (именно такой поверхностью и является псевдосфера), и тогда уже не оставалось больше никаких сомнений в том, что в этой геометрии, как и в геометрии Евклида, нам нечего бояться противоречий.

- 272 -

- Ну, как Илюша? - сочувственно спросил Радикс. - Способен ли ты после этого соображать дальше или нет?

- Сейчас! - ответил Илюша. - Я только еще попробую.

Мальчик взял волшебно-математический аппаратик, измеряющий кривизну, и как только он приложил оловянный листик к поверхности гиперболоида, немедленно стрелка аппаратика пошла от буквы "Е" в другую сторону - это была самая настоящая отрицательная кривизна.

- Ясно? - спросил Коникос.

Илюша кивнул и сказал:

- Трудновато. Но мне кажется, я все-таки кое-что понял.

А теперь я хочу наконец про Архимеда послушать!

- Ну что ж! - раздумчиво промолвил Коникос. - Теперь-то, пожалуй, уж можно... Да, постой-ка! Я вот еще что хотел тебе сказать, чтобы ты не забыл. Дело в том, что наш эллипсоид вращения можно еще сжать сверху вниз так, чтобы его круглое сечение тоже обратилось из круга в эллипс. И тогда из эллипсоида вращения получится трехосный эллипсоид, у которого все три оси но всем трем измерениям, то есть и в длину, и в ширину, и в вышину, разные или по крайней мере могут быть разные. Ясно, что как ни рассекай его по всем этим трем перпендикулярным направлениям, в сечении получишь эллипс. Например, кусочек туалетного мыла, который в просторечии нередко называют обмылочком, обычно как раз и имеет форму трехосного эллипсоида! Или морские камушки, обкатанные морскими волнами...

- Как хорошо, - сказал Илюша, - что все эти ваши математические чудеса так легко встретить! Подумаешь, какое чудо обмылочек, а оказывается, он родственник самим коническим сечениям! (А про себя подумал: "Вот, значит, почему этот козлоногий человечек с флейтами говорил о морских камушках!") Постойте-ка, - продолжал он, - вы мне обещали показать, как делается псевдосфера.

- Совсем из головы вон! - сокрушенно сказал Асимптотос. - А ведь и вправду обещали! Поди-ка, Коникос, поищи-ка, где у нас там трактриса завалилась.

Не прошло и минуты, как Коникос вернулся весьма смущенный и раздосадованный.

- Пропала, скажи на милость! Истинное наказание!

- Ничего, - успокоил Асимптотос. - Подумаешь, какое горе! Возьмем да и новую сделаем.

Коникос принес довольно большую цепь с тяжелыми звеньями, вроде корабельной, и повесил ее за два конца на стену.

Цепь угрюмо повисла, образуя почти дугу, открытую сверху.

- 273 -

- Похоже на параболу, - шепнул Илюша Радиксу.

- Неверно. Впрочем, подобную ошибку в свое время сделал даже сам Галилей, так что тебе и подавно простительно.

Однако все же ты должен запомнить, что это вовсе не парабола, а так называемая цепная линия. Она только на маленьком участке у вершины очень похожа на параболу.

- К этой цепи у нас, - сказал Асимптотос, - прилажена особая ниточка, гибкая, нерастяжимая. Сейчас я ее отделю от цепи. Это особый способ чертить кривые - при помощи такой ниточки. Ты умеешь чертить по линейке, умеешь чертить циркулем, а это еще один способ чертить. Смотри внимательно!

Я отщипну эту ниточку в самой точке вершины цепи, то есть цепной линии, и буду, крепко все время натягивать нить, следить за тем, какую кривую опишет конец нити в той плоскости, в которой находится кривая. Так вот эту кривую, которую опишет конец нити, мы называем эвольвентой данной исходной, начальной кривой. А кривая, с которой надо сматывать нить, чтобы получить некую требуемую кривую, называется эволютой этой последней.

При этих словах Асимптотос отщипнул что-то от цепи в самой нижней ее точке. В руках его оказалась тонкая блестящая нить, которую наш ученый старичок начал как бы сматывать с цепи, все время крепко натягивая нить вниз и направо.

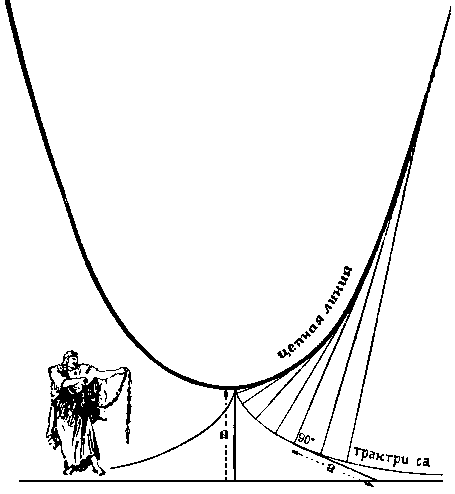
- 274 -

И конец нити послушно начертил новую своеобразную кривую, совершенно непохожую на ценную линию.

- Ну вот тебе и трактриса! - радостно воскликнул Коникос. - Сам Лейбниц дал ей это имя.

- Так что трактриса есть эвольвента цепной линии? - спросил Илюша.

- Точно! - отвечал Коникос. - Оказывается, ты кое-что соображаешь!

- Но если, - снова начал Илюша, - это особый способ чертить кривые, то должен ведь быть какой-нибудь общий прием, чтобы начертить так любую кривую?

- Это не так уж сложно, - вмешался Асимптотос. - Ты вот посмотри на перпендикуляры к касательным, которые именуются нормалями данной кривой.

- Радиус окружности и есть ее нормаль? - спросил Илюша.

- Справедливо! - отвечал Асимптотос. - Посмотри и заметишь, что касательные эволюты суть не что иное, как нормали эвольвенты. Поэтому, если тебе задана эвольвента, то построй к ней побольше нормалей: все они будут касательными к эволюте, которую эти касательные очень ясно обозначат на чертеже. Это будет кривая, плавно огибающая все эти прямые, касаясь их.

- Эволют у нас девать некуда, - заметил Коникос, - целая кладовая. Но можно еще и по-другому все это проделать.

Возьми отрезок прямой, приложи его в одной точке к шаблону эволюты и кати его по кривой, только чтобы он не скользил.

Вот ты и получишь эвольвенту безо всякой нити, потому что какая-нибудь заранее отмеченная точка на катящемся отрезке вычертит эвольвенту.

Радикс сейчас же объяснил Илюше, что он на досуге и сам все это может проделать. Надо взять топкую и нежесткую нитку примерно в сорок сантиметров длиной, намочить ее и мокрую повесить на стену на два гвоздика, которые вбиваются на расстоянии около пятнадцати сантиметров друг от друга.

А на то место, куда мы повесим нить, надо заранее прикрепить кнопками лист белой бумаги. Затем следует аккуратно начертить кривую, которую образует мокрая нитка, - это и будет приблизительно цепная линия. По этому чертежу надо изготовить картонный или фанерный шаблончик. В верхнем его углу следует закрепить нитку, обвести се по краю шаблона, а у вершины сделать петельку. Если теперь взять карандаш (сделав предварительно маленькую зарубку на графите) и вставить в эту петельку, то карандаш - если осторожно сматывать нитку - вычертит трактрису.

Коникос взял кривую и приладил ее, кряхтя и ворча, к диаграмме с картезианскими осями, повернув ее на девяносто градусов.

- 275 -

- Трактриса, - сказал он, передохнув после своей нелегкой работы, - это кривая весьма древнего происхождения.

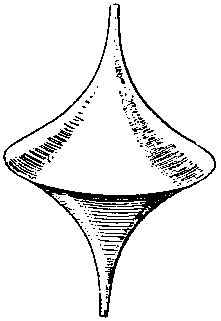
Псевдосфера

Одно из замечательных свойств ее заключается в том, что если к ней провести касательную в любой точке, то расстояние по касательной от точки касания до некоторой прямой будет постоянным (удаляясь от своей вершины, трактриса неограниченно приближается к этой прямой, и на нашем чертеже эта прямая будет перпендикулярна к оси цепной линии). Если поместить конец нити на расстоянии а от горизонтальной прямой, а потом другой ее конец тянуть вдоль этой прямой, то первый конец и опишет трактрису. Отсюда и название ее (от латинского слова "тянуть"). Если же теперь мы прикрепим трактрису по ее горизонтальной оси к Центрифуге, то мы и получим искомую поверхность вращения, то есть именно псевдосферу.

И действительно, как только прикрепили трактрису к Центрифуге и пустили последнюю в ход, получилась псевдосфера, каковую Асимптотос спокойно снял со станка и разрезал пополам, затем добыл откуда-то резиновую нитку и влез внутрь того вогнутого конуса, похожего на опрокинутый бокал, который представляла собой полупсевдосфера.

- 276 -

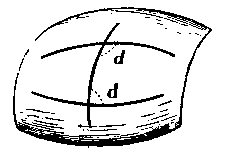
На выпуклой поверхности два перпендикуляра сходятся

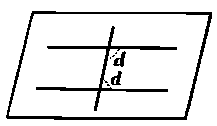
На плоскости два перпендикуляра не сходятся и не расходятся

Поверхность была довольно прозрачная, и Асимптотоса было отлично видно. Намазав резиновую нитку сажей, он натянул ее на поверхность полупсевдосферы и, щелкнув ниткой, получил одно ребро треугольника снизу вверх, направо от основания к вершине - ровную темную черту. Затем он так же обозначил другое ребро треугольника сверху, от вершины вниз направо, подмигнул Илюше и сказал:

- Так как я имею дело с поверхностью отрицательной кривизны, то, для того чтобы провести основание треугольника, я должен, очевидно, выбраться из-под псевдосферы снова наружу.