Схолия Девятнадцатая
Схолия Девятнадцатая
особенно примечательна тем, что в ней наш доблестный путешественник знакомится с историей мнимых человечков, узнает, что произошло в городе Болонья в XVI веке, как павиан умеет бросать камни, и что об этом думали математики. Илюша в этой схолии не раз попадает в затруднительное положение, и только - его закадычные друзья спасают его от снежной бури, а затем Илюша снова встречает своего старого знакомого Дразнилку, который и помогает нашему герою решить трудную задачу.
Голубоватое поблескивание откуда-то сбоку неожиданно оказалось снова симпатичной фигуркой Мнимия Радиксовича.
Он очень любезно улыбнулся и заметил:
- Чудесные звезды, не правда ли?
- Мне очень хотелось бы, - сказал Илюша, - чтобы вы еще как-нибудь показали мне подробно, как вы, мнимые человечки, возникаете из квадратного уравнения?
- Вы ведь знаете, - начал свой рассказ Мнимий, - что, когда квадратное уравнение "не решается", мы получаем два комплексных корня, причем они таковы, что действительные части их равны, а мнимые отличаются по знаку:
а + bi; а - bi.
Такие комплексные числа называются сопряженными.
- 414 -
Сопряженные комплексные числа обладают одним замечательным свойством: их сумма так же, как и их произведение, является действительными числами. Это нетрудно проверить!
- Знаю! - откликнулся Илья. - Я уж пробовал. Мне кажется, как будто, что при перемножении мнимых чисел разные знаки дают плюс, а одинаковые минус...
- Ученые, - продолжал Мнимий, - сперва, в семнадцатом веке, догадались, а через два века и доказали, что если принимать в расчет все корни уравнения, и действительные и комплексные, то вместе их будет всегда столько же, сколько единиц в показателе степени старшего члена уравнения. Это положение, чрезвычайно важное для алгебры, обычно называется основной теоремой алгебры[34]. Попутно выяснилось, что комплексных корней всегда бывает четное число, и у каждого такого корня имеется сопряженный комплексный корень.
А то, что вы хотите узнать, можно показать на геометрическом примере. Сначала мы возьмем обычную декартову плоскость, затем еще одну, которая будет комплексной, и она же будет полупрозрачной... А вы, юноша, дайте мне квадратное уравнение поудобней!
- Пожалуйста! - не задумываясь, ответил наш герой, -
х2 - 8х+ 15 = 0.
Три и пять. Лучше не придумаешь.
- Сойдет, - ответил Мнимий. - Дальше так: пусть перед нами встанет первая плоскость, на ней оси деления и парабола. А комплексная плоскость пусть станет перед первой вплотную. Она полупрозрачная, и через нее мы отлично увидим первую.
Так все и случилось. Сперва возникла обычная плоскость, причем ось абсцисс была голубая, а ось ординат розовая, потом возникла и темно-синяя парабола. А на делениях ( + 3) и (+5), там, где были корни квадратного уравнения, где парабола пересекла ось абсцисс, ярко горели две блестящие оранжевые точки.
- Вот и корни! - сказал Илюша.
- А теперь мы сотворим и комплексную.
И действительно, тут же, поправей, возникла еще одна плоскость, не очень заметная, матовая. На ней были тоже две взаимно перпендикулярные оса, действительная и мнимая, только они были совсем тоненькие. В начале координат сияла зеленая точка.
- 415 -
- Подвиньтесь! - вежливо попросил Мнимий.
И тут комплексная плоскость подвинулась налево и стала так аккуратно, что оси на том и на другом чертеже почти слились (они ведь были в одном масштабе!), но все было очень хорошо видно через вторую полупрозрачную плоскость.
- А зеленая точка на нуле, - сообразил мальчик, - означает, что ничего мнимого пока еще нет?
- По-видимому, так... - раздался торжественный шепот прямо из самого экрана: волшебные чертежи, оказывается, отлично умеют говорить!
- Итак, - продолжал Мнимий, - следите за мной хорошенько, и вскоре все станет ясно. Вот перед вами парабола!
Она, как вы знаете, прекрасная гречанка, и от роду ей очень много лет. Для того чтобы все было не так хитро, мы будем рассматривать ее в таком виде, что коэффициент при иксе во второй степени будет равен единице.
- То есть, - подхватил Илья, - мы берем выражение
ах2 + bх + с
и делим все члены на а.
Теперь перед Илюшей сиял график квадратного трехчлена, то есть чертеж параболы, обращенной вершиной вниз, ее ось стояла вертикально, и вершина параболы была ниже оси абсцисс (которая, как мы знаем, горизонтальная). Парабола пересекала ось абсцисс дважды. Недалеко засветилось и само уравнение:
х2 - 8х+ 15 = 0.
- А какие у нас корни? - спросил Мнимий.
- Два действительных корня, потому что парабола пересекает ось абсцисс два раза, - отвечал мальчик.
- Справедливо. Теперь я попрошу параболу подняться немножко повыше.
Парабола охотно послушалась, и две оранжевые точки на горизонталях стали сближаться; и вот уже вершина параболы только касалась оси абсцисс в одной точке. Две оранжевые точки сошлись в одну.
- А теперь? - спросил Мнимий.
Рядом уже светилось и уравнение:
х2 - 8х + 16 = 0.
- А теперь, - отвечал Илья, - два одинаковых действительных корня, оба равны (+4).
- 416 -
- Так. Согласен. Попрошу еще вверх немного.
Послушная парабола согласилась и на это. И теперь вся она поднялась выше оси абсцисс, не касаясь ее. Вершина параболы по-прежнему висела над делением оси абсцисс, равным четырем. Однако как только вершина параболы вздумала оторваться от горизонтали, немедленно оси на полупрозрачной комплексной плоскости стали еще ярче, а зеленая точка в начале координат вспыхнула посветлее. Едва лишь горизонталь и вершина параболы расстались друг с другом, эта точка немедленно раздвоилась. И теперь уже две зеленые точки медленно поползли: одна вверх по мнимой оси, а другая по той же оси вниз. Затем обе эти точки остановились против деления три, только одна стояла против (+3), а другая против (-3).
- Ну-с, - произнес Мнимий, - я вас слушаю.
- Тут, - сказал Илюша, - оба корня комплексные. И они, конечно, сопряженные. Один будет равен (4 + 3i), а другой (4-3i). Если теперь открыть скобки в выражении
[x - (4 + 3i)] [х - (4 - 3i) ] = 0,
то получится вот что:
х2 - 8х + 25 = 0.
Этому уравнению соответствует парабола вот такая, как сейчас на нашем чертеже. А почему это так, сообразить нетрудно.
Ведь если написать:
[x - (a + bi)] [х - (a - bi) ] = 0,
то открой скобки и получишь:
х2 - 2ах+ (а2 + b2) = 0.
Вот и все! Проверить - одна минута.
- Точно! -подтвердил Мнимий. - А больше вы ничего не замечаете?
И вот только тут наш герой усмотрел, что парабола отразилась ниже действительной оси и висит там вершиной вверх.
Так что теперь уже перед ним были как бы две параболы...
А из самого начала координат (там, где пересекались обе оси) ползет яркий лиловый пунктир со стрелочкой на конце. Он добрался до точки с координатами D, 3), и стрелочка его остановилась, как только коснулась этой точки.
- 417 -
Илюша обернулся к Мнимию, но, к своему удивлению, обнаружил, что его приятель... исчез бесследно! Но когда он невольно слова перевел глаза на чертеж, он с удовольствием заметил, что лиловая стрелочка уже превратилась в самого Мнимия, который очень весело ему кивает из глубины чертежа!
- Вот я каков! - крикнул Мнимий из чертежа. - Могу вырасти, если парабола поднимется вверх...
Парабола стремительно рванулась ввысь, Мнимий, ринувшись за ней, вытянулся, стал длинный-длинный и страшно важный, ибо вершина параболы ушла куда-то очень высоко, а Мнимий остановился на 92-м делении по мнимой оси. Пока Мнимий удлинялся, в записи сверкающего уравнения значение свободного члена начало быстро увеличиваться (а коэффициент при неизвестном в первой степени оставался тем же).
И в конце концов вот что получилось:
х2 - 8х + 8480 = 0.
- А если вам так уж хочется, я могу стать и поскромнее!
Парабола стала, не торопясь, опускаться и остановилась против деления 19 на вертикальной оси.
Тут же засветилось и уравнение:
х2 - 8х + 377 = 0.
- Могу и вовсе исчезнуть!
Парабола опустилась до самой оси абсцисс, коснулась ее, и Мнимий исчез.
Илюша обернулся, и оказалось, что Мнимий уже снова стоит рядом с ними.
- Теперь вам ясно, как мы возникаем? Но вы, надо полагать, уже заметили, что, как только парабола оторвется от оси абсцисс, сейчас же снизу, как говорят, на нижней полуплоскости (потому что ось абсцисс делит плоскость пополам!), возникает ее отображение, а вместе с ним и мой сопряженный братец-близнец. Вот и все. Очень просто!
Парабола на чертеже снова поплыла вверх, а внизу опять засияло ее отображение, и тут же появилась еще одна лиловая стрелочка, направленная из начала координат вниз.
- Понятно, - сказал Илюша, - если сложить эти два вектора, то мнимые их части с разными знаками уничтожат друг друга и получится удвоенная величина действительной части.
Раздели пополам, и получишь точку, над которой находится вершина параболы. Все в порядке!
- Рад стараться! - отвечал Мнимий. - Конечно, парабола может выше оси абсцисс стоять и вершиной вверх, а не вниз, но, в общем, это безразлично.
- 418 -
- А почему вы говорите "отображение", а не "отражение"?
- Да так уж повелось от тех времен, когда вместо "отразилось" говорили "отобразилось". Это не так уж давно было, примерно во времена Лобачевского. Это слово встречается и у Гоголя. Имейте также в виду, что только под пером великого Эйлера мы получили все права гражданства в математике.
С вашего разрешения мы вернемся сейчас еще на некоторое время к решению уравнений. Тут вы и узнаете, как мы появились на белый свет, что мы помогли узнать математикам и как они с нашей помощью стали открывать одну тайну за другой.
- Ну, Илюша, как дела? - спросил с усмешкой Радикс-
Тебе все ясно?
- Не очень! - признался Илья со вздохом. - Нет, не очень.
А нельзя ли как-нибудь так придумать, чтобы не было двух разных плоскостей, а то меня путает, что их две? Ведь на самом-то деле это одно уравнение, а вовсе не два?
- Справедливо! - согласился Мнимий. - Действительно, одно.
- Может быть, попробовать еще? - предложил Радикс. - Возьмем еще одну параболу. Уравнение ее напишем так:
z = х2 - 8х + q.
Значит, свободный ее член у нас обозначается теперь буквой q.
Если попробовать решить квадратное уравнение:
х2 - 8х + q = 0,
мы получим...
- ...вот что! - сказал Илюша и написал:
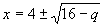
Значит, пока наше q меньше шестнадцати, корни будут действительные, а если q больше шестнадцати, то комплексные.
- Разумеется! - согласился Мнимий.
- А когда q равно в точности шестнадцати, парабола только касается оси абсцисс в точке, равной четырем. Если же q равно нулю, то оба корня будут действительные - один равен нулю, а другой - восьми. Но только... как же нам теперь увидать еще и комплексные корни?
- Не спеши, - отвечал Радикс, - сейчас мы все это соорудим. А уж ты следи внимательнее за этим новым тонким и умным волшебством. Нам ведь нужно определить, существуют ли такие комплексные числа, чтобы при подстановке их в левую часть уравнения мы получили бы действительное число? Существуют ли, а если да, то каковы они?
- 419 -
- Тогда, - отвечал Илья, поразмыслив, - нам придется подставить в левую часть комплексное число (z+iy), а затем посмотреть, что из этого выйдет. Получится, значит, так:
r = (х + iy)2 - 8(х + iy) +q= (x2-y2-8x + q) + i{2xy-8y).
Мне кажется, что это выражение может оказаться действительным единственно только в том случае, если вся скобка, на которую умножается i, будет равна нулю.
- Так! - согласился Мнимий. - Верно. Это дело! А в каком случае так оно будет?
- Если, - отвечал мальчик, - я перепишу эту скобку немного иначе:
2ху - 8у = 2у(х - 4),
то ясно, что это может произойти только в двух случаях, либо игрек равен нулю (ну, тут все и так ясно, говорить нечего!), либо икс равен четырем.
- Хорошо! - сказал Мнимий, улыбаясь. - Теперь уж у нас все готово, и мы можем приступить к нашему волшебству, которое нам все и покажет в полной наглядности, как оно и полагается в нашем волшебном царстве, построенном на поучение самым любознательным и дерзновенным юношам...
- Дерзновенным! - с усмешкой повторил Радикс. - Но я слышал, как друг Пушкина, замечательный русский поэт и мыслитель Евгений Баратынский однажды написал:
Надейтесь, юноши кипящие!
Летите, крылья вам даны...
А ведь так оно и полагается, дружище, в нашем светлом волшебном и вполне серьезном царстве для любознательных ребят!
- Ура! - закричал Илья. - Давайте ваше новое волшебство. Вы уж такие волшебники...
- Потише ты! - возразил Радикс. - Не спеши. Поспеешь!
Это будет штучка довольно затейливая. Начнем с того, что это новое волшебство будет не на плоскости, а в пространстве.
- В трехмерном? - робко пропищал Илья.
- Неужто тебе трехмерного мало? - свирепо огрызнулся Радикс. - Можно и четырехмерное, да ты испугаешься! Ну!
Смотри во все глаза.
Радикс медленно и важно махнул рукой. И тотчас же перед Илюшей возникла плоскость, где были начерчены обыкновенные декартовы координаты (икс, игрек, как оно и полагается!).,
- 420 -
Направо от начала координат была проведена еще одна прямая, параллельная оси игрек, как раз в том самом месте, где икс равнялся четырем.
- Смекаешь? - спросил Радикс, указав Илье на эту четверку.
- Смекаю... - несмело откликнулся Илья, - то есть это та самая четверка, при которой моя скобка становится равной нулю? Так или нет?
- Именно! - отвечал ему его друг.
Смотри далее... Да смотри в оба! Полагаем твое q равным нулю... А теперь...
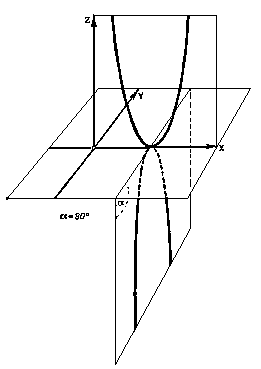
Тут Илюшина плоскость потихонечку повернулась и легла горизонтально, повиснув в воздухе примерно в сантиметрах шестидесяти от пола. Да так и застыла. Как только это произошло, из каждой точки креста, образованного осью иксов и новой прямой, которая пересекла ось иксов в точке, равной четырем, начали постепенно расти перпендикуляры к этой самой плоскости, которая и была плоскостью (х + iy), то есть плоскостью комплексных векторов (следи внимательней!).
И тут, опираясь на эти перпендикуляры и пересекая ось иксов (там, где игрек равен нулю), из концов этих перпендикуляров выросла парабола. Самая настоящая парабола с уравнением:
z = х2 - 8х.
А уравнение сейчас же засветилось справа сбоку красным огнем, чтобы Илья не путался! Затем (смотри хорошенько!) и-* прямой в новой вертикальной плоскости (опять же перпендикулярной к висящей в воздухе плоскости комплексных векторов) возникла еще одна парабола с уравнением:
z = 42 - у2 - 8•4 = - у2 - 16.
- 421 -
Теперь перед Илюшей было уже две параболы. Мнимий подошел совсем близко к этой высоковолшебной модели и мягким прикосновением своих волшебных пальчиков жестко скрепил эти две параболы так, что они оказались соединенными и своих вершинах, а плоскости их оказались перпендикулярными одна к другой.
- Видишь?- спросил Радикс. - Теперь смотри, что у нас будет получаться далее, когда мы начнем увеличивать постоянный член, то есть это твое q. Следи внимательно за этой фигурой из двух соединенных парабол, не отрывая глаз.
Вся эта сложная параболическая механика начала двигаться и прошла вверх на шестнадцать делений. Как только она остановилась, тотчас же сбоку справа засветилось ее уравнение красным огнем:
z2 = x2 - 8x+ 16= {х - 4)2.
А слева появилось еще одно уравнение (для другой параболы) - зеленое:
z = -у2.
- Внимание! - громко провозгласил Мнимий. - Если теперь далее мы еще будем увеличивать ваше q, то первая наша парабола уже не будет больше пересекать плоскость (x + iy), но зато нижняя парабола пересечет ее как раз дважды, в двух точках, которые, по мере увеличения вашего q, будут разбегаться в разные стороны по прямой (х = 4). Вот вам, мой юный друг, настоящая, подлинная картина того, как могут возникать комплексные корни квадратного уравнения. Поняли?
- Ох! - произнес Илюша, утирая пот со лба. - Что-то такое я сообразил. Но вы бы хоть еще разок повторили!..
И снова перед Илюшей возникла вся эта волшебно-наглядная математическая интермедия с самого начала до самого конца. Теперь Илюша как будто стал разбираться.
- Но как странно они скреплены, эти параболы, - сказал он, - они ведь зацепились одна за другую, точно они надеты одна на другую, как вот... если взять две дуги... ну, самые обыкновенные, которые на лошадей надевают... да и поддеть их так, чтобы одна висела на другой. Верно я говорю или нет?
- Точно так! - отвечал равнодушно Радикс[35].
- 422 -
- А все-таки, - снова начал Илюша, - я ерошу еще мне кое-что разъяснить. Про корни я теперь понял, но кое-что более общее мне неясно. Вы, Мнимий, помогла открыть тайны. .. Но ведь вы сами - тоже изобретение математиков?
- Не совсем изобретение. Мы - открытие! Природа царит во всем мире, а у нее свои законы. Труд человеческий в значительной мере определяется этими же законами. Ведь не одни человек трудится - птица вьет гнездо, пчела строит очень точные шестигранные соты, паук плетет многоугольники паутины, крот строит тоннели и так далее. Человек с помощью Математики изучает эти законы, и когда он открывает нечто новое в строении этих внутренних связей, неправильно говорить, что он что-то "изобрел". Он открыл то, что всегда лежало в основе некоторых явлений природы.
- Трудно понять, - произнес со вздохом Илюша, - как это такое: уравнение и природа? При чем тут природа?
- А когда вы бросаете камень, ведь он летит по параболе, не так ли? А парабола алгебраически - это квадратное уравнение. А те, кто путешествовал по Африке, рассказывают, что большие обезьяны, павианы, очень хорошо умеют бросать камни. Однако камень не рассуждает, кто его бросил - ученик седьмого класса или павиан, все равно он летит по параболе!
Илюша уставился на Мнимия и не знал, что отвечать.
- Ну как, Илюша? - спросил Радикс. - Долетел до тобя этот камушек?
- Не знаю! - ответил в недоумении Илюша. - С павианом действительно как-то странно получается...
- Крепись! - посоветовал Радикс. И добавил: - Был в древности такой философ, Платон. Он любил пересказывать речи другого философа, своего современника, Сократа. И вот в одном из сочинений Платона Сократ говорит, что человек разумный "будет заниматься астрономией, как и геометрией, для того чтобы ставить задачи разуму", но не будет терять время на прихотливо-изящные разглагольствования о красоте звездного неба. Нет, он будет "искать истину" в явлениях подобного рода. А истина эта, как легко догадаться, заключается именно в математических законах движения небесных светил. Задача оказалась необычайно трудной и, не взирая на все грандиозное развитие древнегреческой математики, грекам полностью одолеть ее не удалось. Решение было получено только в семнадцатом веке нашей эры. Как ты знаешь, эти решения были связаны в первую голову с именем Иоганна Кеплера, одного из великих основателей математического естествознания, на основе которого построена вся современная цивилизация.
- Итак?.. - переспросил Мнимий.
- Не знаю... - с усилием выговорил Илюша. - Как-то все это в голове не укладывается
- 423 -
- Постой-ка, - сказал Радикс, - пожалуй, я приводу еще один пример, с которым ты уж спорить не станешь. Конечно, и юноша из седьмого класса и павиан - существа, не лишенные некоторого смысла, и, пожалуй, ты будешь колебаться, можно ли назвать их действия просто действиями Матушки Природы. Так вот тебе еще один пример, где одушевленные существа уж совсем не принимают никакого участия: по горе бежит маленький ручеек, наконец добегает до крутого обрыва и низвергается, скажем, метров на двадцать с лишним (высота шестиэтажного дома!) тоненьким водопадом в одну струйку. Ясно ли тебе, что и эта водопадная струя будет иметь строение той же самой параболы? Это ты можешь проверить самым простым опытом с резервуаром, водой и резиновой трубкой. Отсюда ясно, что парабола имеет в мире, независимо от человека и его мыслительных способностей, совершенно объективное существование, независимое от нас.
Следовательно, когда человек нашел эту кривую, он сделал открытие- он нашел формулировку важного закона Природы.
А обстоятельство, что сама кривая (у Аполлония Пергейского в древности) была найдена путем геометрического рассуждения, умозрительно, и только потом (у Галилея) приняла характер закона Природы, значения не имеет. Одно только можно вывести из этого поучительного сопоставления, что логическое развитие (и расширение) математических образов и истин потому и ведет к открытию орудий математического естествознания, что даже самые первые положения математики непосредственно возникли из человеческого опыта и размышлений над результатами этого многообразного опыта.
- Вот и опять получается, - заявил Илюша, - что математика - это опытная наука...
- ... опирающаяся в своих построениях на здравый человеческий рассудок, на логику, - добавил Радикс, - и постоянно проверяющая своп построения на решениях практических задач. Когда-то Аристотель учил, что человеку нужна свобода, но не просто свобода, а обдуманная свобода, разумная, такая, которая ведет к полезным результатам. И вот, обдумывая свои удачные и полезные действия, человек и находит математические орудия, которыми он покоряет Природу.
- 424 -
Вот примерно как! Конечно, что ни дальше, тем оно становится сложнее, но, как говорится, чем дальше в лес, тем больше дров! Ну, следует еще отметить, что летит тело по параболе только в пустоте, то есть при отсутствии сопротивления воздуха, в полном безветрии, а иначе получается хотя и близкая к параболе кривая, но все-таки не парабола. Хотя все математические образы, которые мы в рассуждениях считаем абсолютно точными, на практике не могут иметь такую неограниченную точность, однако самое важное и самое основное в явлении они выявляют с большой силой.
Внезапно откуда-то донесся знакомый мелодичный свист древних флейточек, раздался легкий топот маленьких копытец, и голос небезызвестного Илюше Фавна лукаво произнес:
- А камушки? Морские камушки?
- Что такое? - вопросил Радикс. - Какие это камушки?
- Ах да! - воскликнул мальчик. - Морские камушки, обкатанные волнами, как трехосный эллипсоид!
- Верно! - подтвердил Радикс. - Вот тебе и еще пример довольно сложного геометрического тела, который сооружает сама природа.
- В общем, ясно! - примирительно заявил Мнимий. - И я предлагаю, приняв в общем выводы моего почтенного папаши к сведению и руководству, перейти к нашим очередным делам. Мне хотелось бы обратить ваше внимание на ряд особо значительных фактов из истории нашей науки. Хотите ли вы меня выслушать?
- Очень даже! - отвечал Илюша. - Когда вы мне все здесь рассказываете о развитии нашей науки от древности и чуть ли не до наших дней, то выходит более понятно...
- Хорошо, - заметил Мнимий, - насчет "чуть ли не до наших дней" - это немножко, пожалуй, слишком, ибо "наши дни" в математике - это уж очень трудно! Но кое-что наметить можно[36]. Только вы слушайте внимательно и сейчас же переспрашивайте без стеснения, как только почувствуете, что теряете нить моего рассказа. Согласны?
- Вполне!
- Итак, надо отметить, что в науке время от времени бывают некоторые нежданно разительные перемены. То есть если рассуждать впоследствии, то поймешь, что они не такие уж "нежданные", а, наоборот, подготовлялись издалека, хотя самое решение вопроса сперва кажется совершенно неожиданным. Понимаете вы меня?
Тут уж Илюше пришлось признаться, что он не очень понимает, о чем идет речь.
- Ну вот, - сказал, задумываясь чуть не на каждом слове, Мнимий, - возьмем алгебру. Самую обыкновенную, которую вы в школе учите. Это просто буквенное исчисление, не так ли? А ведь всякий ученик прекрасно знает, какое это облегчение для решения задач.
- 425 -
- Конечно, - согласился Илюша, - алгебраически решать задачи гораздо проще, чем с арифметикой возиться!
- Согласен! Но давайте разберем, как это случилось.
Ведь всякий замечал, что много есть на свете задач очень друг на друга похожих, то есть, как говорится, задач одного типа. Вот на этом-то наблюдении и родилась алгебра. Надо было еще получить некоторый толчок - догадаться, что вместо чисел можно употреблять буквы. Новое в науке родится путем наблюдения над своей собственной работой - то есть над решением разных задач, - а затем путем выводов из этих наблюдений. И, наконец, путем построения такого общего способа (или метода), который помог бы нам воспользоваться тем, что мы нашли наблюдением, а метод этот и был буквенным исчислением.
- А он откуда взялся?
- Он был в зачатках еще у египтян и у греков. Затем индусы, а за ними арабы заметили, что способы решать арифметические задачи могут быть сведены к нескольким типам - ну, хотя бы к уравнениям с одним неизвестным, - и описали это словесно. Возникла так называемая риторическая алгебра, не очень, конечно, удобная, но все-таки более совершенная по сравнению с простой арифметикой[37]. А уж потом пришли и буквы, но путь им был расчищен при помощи риторической алгебры.
- Значит, так, - решил Илюша, - сперва мы наблюдаем, замечаем важные особенности при пользовании старыми способами, а затем на основании этих наблюдений и рассуждений уже строится новая наука, то есть новый ее раздел.
- Правильно, - согласился Мнимий, - такие весьма важные перемены и бывают, как я выразился, "нежданно разительными". Такие нововведения, обобщающие большой опыт, дают огромные результаты и сразу двигают науку вперед.
Проходит несколько десятилетий - и науку уже узнать нельзя, так быстро она развивается на новом рубеже. Арабы построили алгебру, ее узнали в Европе, а затем сразу раздаются мощные голоса Виеты и Декарта. И вот уже та алгебра, которую вы учите в школе, построена. И все становится иным, появляются возможности строить еще нечто совершенно новое.
- А когда это случилось?
- Арабская алгебра родилась примерно в восьмом или девятом веках, а распространять ее в Европе стали примерно с двенадцатого века. Я имею в виду славного Ал-Хорезми.
- 426 -
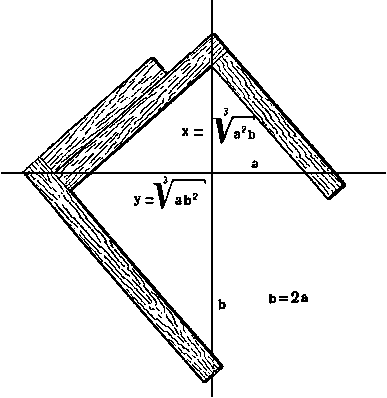
Прибор Платона.
В это же время появляются сочинения европейцев, уже освоивших алгебру. В начале шестнадцатого века все это было в Европе освоено, развито и вот тут-то Европа встает на новый путь развития. Сочинения Архимеда и Аполлония переведены и напечатаны. Начинаются новые труды. Они как бы вмещают все, что Европа унаследовала от арабов (а стало быть, и от индийцев) и от Древней Греции. И теперь начинаются плодотворнейшие труды по объединению того и другого. Если труды европейцев, которые привели к интегральному и дифференциальному исчислению, были завершением ТРУДОВ древних, шедших в том же направлении, то с шестнадцатого века началось еще одно движение: новые достижения риторической алгебры были впервые успешно применены к решению алгебраических уравнений высших степеней, например кубических.
- А раньше их совсем не умели решать? - спросил Илюша,
- 427 -
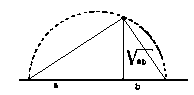
Одна средняя пропорциональная и один прямой угол.
- Опыты и частные решения были. Мы вам рассказывали о способе Двух средних пропорциональных и о способе Менехма (в Схолии Пятнадцатой - способ двух парабол). Но все это были геометрические способы, которые не обладали общностью, то есть не могли быть применены для решения любой задачи, которая приводит к кубическому уравнению.
- Мы рассматривали, кажется, тогда, - заметил Илюша, - пропорцию Гиппократа:
а : х = х : у = у : b
и ее алгебраическое решение, а как греки решали, мы как будто не говорили.
- Ну что ж, - сказал Радикс, - можно и это припомнить.
Для решения этой задачи - для удвоения куба - можно пользоваться так называемым "прибором Платона", который легко представить тебе в виде двух плотничьих наугольников, то есть деревянных прямых углов, как бы прямоугольных треугольников без гипотенузы. Начинаем с чертежа, где изображены две прямые, пересекающиеся под прямым углом. Затем берутся два угольника и прикладываются друг к другу так, чтобы они образовывали два прямых угла. Нетрудно рассудить, что если даны длины отрезков а и b, то из двойной пропорции Гиппократа, которую я только что привел, можно получить:
х3 = a2b; у3 = ab2;
и, положивши b = 2а, получаем:
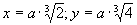
Все это так сложно формулируется потому, что у Евклида в его Началах (книга IX) степени - квадраты, кубы и так далее - так и вводятся, через пропорции, и опираются на известные свойства геометрической прогрессии:
1, x, x2, x3, 4 ... xn
- 428 -
где ясно, что каждый член является средней геометрической между двумя своими соседями справа и слева, как например:
х2 = ?(х • x3 )
а четыре последовательных члена связаны двойной непрерывной пропорцией:
1 : х = х : х2 = х2 : х3,
которой и пользуется Гиппократ. Теперь возвращаюсь к построению: циркуль дает одну среднюю пропорциональную, которую мы разбирали в Схолии Пятнадцатой, тогда как два прямых угла действуют словно два объединившихся циркуля, они дают нам разом две средних, как это ясно из другого чертежа. Прямой угол мы всегда можем себе представить опирающимся на диаметр некоторой окружности, не так ли?.. А если у нас имеются два прямых угла, причем их всегда можно сдвигать и раздвигать так, что эти диаметры воображаемых окружностей могут изменяться (и при этом независимо друг от друга), то мы получаем особый прибор вроде двоякого циркуля, который может дать нам сразу две средние пропорциональные, те самые, которые требуются для пропорции Гиппократа.
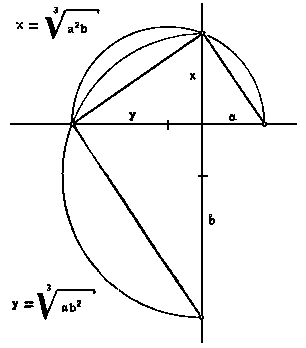
Принцип прибора Платона.
- 429 -
- По-моему, - сказал Илья, внимательно осмотрев чертежи Радикса, - как будто все правильно. Какой интересный этот способ двух прямых углов! И если а = 1, то икс и будет корнем кубическим из двух. Все верно.
- Прекрасно! - похвалил Мнимий. - Итак, после этого поучительного примера я могу продолжать свой рассказ. Алгебра дала ученым формулу (а формула - это ведь и есть самое значительное завоевание алгебры!) для решения любого квадратного уравнения. В шестнадцатом веке ученые заинтересовались алгебраическим решением кубического уравнения, о котором еще в начале того же века Лука Пачиоли, итальянец, говорил, что эта задача столь же непосильна для науки, как и квадратура круга. Конечно, надо все-таки принимать во внимание, что наука, развиваясь, ставит себе все более и более сложные задачи, а для их разрешения, понятно, требуются все более сложные способы. Вот с одной такой необычайной сложностью ученые и столкнулись в шестнадцатом веке. Понадобилось без малого триста лет, чтобы разгрызть этот орешек! О нем-то и будет идти речь. Задачка была особенная. Древние почти ничего здесь не сделали, европейцам все пришлось изучать и рассматривать заново. Арабы тоже брались за этот вопрос, старательно изучали частные случаи, многое изучили и придумали, но по части именно алгебраической у них не получилось. Пачиоли прямо говорил, что решение таких уравнений невозможно, ибо они "диспропорциональны", то есть невыразимы с помощью пропорций, что, разумеется, неосновательно, как это ясно из Гиппократова решения задачи о двоекубии. Как неосновательны были и сетования Пачиоли насчет квадратуры круга, но Архимед тогда еще очень был мало известен... И, наконец, в городе Болонье в шестнадцатом веке напали на алгебраическое решение. Оно...
- А какое это было решение?
- А вот сейчас его продемонстрируем. Сперва надо сказать еще несколько слов об одном особом способе решать квадратные уравнения, вам хорошо известные. Вы знаете способ, который построен на выделении точного квадрата. Но можно действовать еще и по-иному. Выходит не хуже. Если уравнение представлено в двучленной форме, то есть вот так:
xn = a
то решить его нетрудно (разумеется, мы полагаем, что а больше нуля, то есть положительное число), какова бы ни была его степень. Надо только извлечь корень данной степени, а это вопрос разрешимый...
- 430 -
- С логарифмами... - подсказал Илюша.
- Точно, - отвечал Мнимий, - именно с логарифмами.
Следовательно, если мы сумеем данное уравнение привести к такому виду, ыы уже никаких особых препятствий не встретим. Уравнение первой степени приводится к двучленному виду проще простого: сделай приведение, перенеси известные в одну сторону, неизвестные в другую - и готово. Посмотрим теперь, как этого достигнуть с квадратным уравнением, которое нам тоже хорошо знакомо. Любое квадратное уравнение можно представить в таком виде:
х2 + рх + q = 0,
ибо, если коэффициент при х2 не равен единице, делим вес уравнение на этот коэффициент - и дело в шляпе! Как быть далее? А что, если уничтожить второй член уравнения с иксом в первой степени? Тогда останется икс в квадрате и свободный член, а нам как "раз и надо получить двучленное уравнение.
Введем новую неизвестную, допустив, что наш икс таков:
x = y + h.
- А что такое h? - с удивлением спросил Илюша.
- Пока что h совершенно произвольное число, но мы сейчас выясним точно, в каком виде оно может нам помочь. Подставим в уравнение новое значение икса и сделаем приведение. Это нетрудно! Получаем:
(y + h)2 + p(y + h) + q = 0;
y2 + y(2h + p) + h2 + hp + q = 0.
Теперь становится ясно: чтобы уничтожить второй член уравнения, надо положить, что коэффициент при иксе в первой степени равен нулю, то есть:
2h + р = 0;
h = -p/2
Подставим в полученное уравнение. Получаем:
y2 + y(-2p/2 + p) +p2/4 - p2/2 + q;
после приведения:
y2 = p2/4 - q
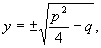
- 431 -
по так как х + у = h, то находим и решение:
x = -p/2 ± ?(p2/4 - q)
Следовательно, наш этот способ - уничтожить один из членов уравнения - вполне целесообразен. Теперь попробуем разобрать, как было решено впервые алгебраически, или, как говорится, "в радикалах", то есть с помощью извлечения корней необходимой степени, кубическое уравнение. Сделано было это в шестнадцатом веке в Италии учеными города Болоньи Ферро, Тарталья и Кардано. Между двумя последними шел долгий спор о том, кто первый сделал это открытие, но мы в эти ненужные споры забираться не будем, тем более что с современной точки зрения все решение не так уж сложно.
- А все-таки, наверно, трудно... - грустно заметил Илюша.
- Не очень! Конечно, поскольку само кубическое уравнение сложнее квадратного, то весь ход решения похитрей. Но тут дело в том, что выясняются некоторые особые подробности. .. Итак, у нас имеется кубическое уравнение, где коэффициент при старшем члене уже превращен в единицу:
х3 + ах2 + bх + с = 0.
Цель снова будет та же самая: придумать такие преобразования, чтобы превратить данное уравнение в уравнение с меньшим числом членов, ибо, как мы видели на примере квадратного, этот прием упрощает задачу. Сперва мы будем поступать так же, как с квадратным уравнением. Положим снова:
х = у + h
и подставим это в наше уравнение. Получим после небольших переделок
у3 + (3h + а) у2 + (3h2 + 2ah + b) у + h3 + ah2 + bh + с = 0.
Теперь снова постараемся обратить коэффициент второго члена (при игреке в квадрате) в нуль, то есть положим, что
(3h + a) = 0; h = - a/3,
откуда
у3 + (-3a/3 + а) у2 + (3a2/9 - 2a2/3 + b) у + h3 + ah2 + bh + с = 0.
- 432 -
или, сделав приведение:
у3 + (-a2/3 + b) у + (2a3/27 - ab/3 + с) = 0.
Теперь для сокращения письма положим:
(-a2/3 + b) = p; (2a3/27 - ab/3 + с) ] = q
аb и запишем окончательно результат в таком виде:
y3 + py + q = 0.
(Если q = 0, то все просто: y1 = 0, у2,3 = ±?-p)
При q ф 0 результат, как ты видишь, разумеется, несколько менее утешителен, чем в случае квадратного уравнения, ибо у нас не два, а три члена. Но как-никак определенное упрощение достигнуто. Как же теперь быть далее? Ясно, что нужно придумать способ, который дал бы возможность обратить выражение ру в нуль, после чего мы и получим двучленное уравнение, то есть то же самое, что было получено для квадратного.
И вот как раз на этом месте болонцам пришла в голову счастливая мысль сделать еще одну подстановку: положить, что у в последнем уравнении можно представить в виде суммы:
у = u + v.
И опять-таки эти величины ими пока что совершенно произвольные. Мы только одно можем сказать, что сумма их есть корень нашего уравнения, который не равен нулю.
- А почему он не равен нулю?
- Сейчас рассмотрим! Попробуем подставить. Получаем:
(u + v)3 + р (u + v) + q = 0.
Смотрите-ка! Теперь видно, что сумма (u+v) не может быть равна нулю, потому что тогда и число q будет равно нулю, а число q, свободный член уравнения, не равно нулю. Теперь откроем скобки и кое-что сгруппируем:
(u3 + v3) + (u + v) (3uv + p) + q = 0.
Такая форма уравнения уже подает нам некоторые надежды!
- 433 -
Может быть, нам удастся уничтожить второй член? Положить, что u + v = 0, мы, как сказано, не можем, но зато спокойно можем допустить, что
3uv + р = 0;
uv = -p/3
но в таком случае наше уравнение превращается в такое:
u3 + v3 = - q.
Следовательно, мы получили два уравнения. Одно из них дает произведение новых чисел u и v, а другое их сумму. Правда, они в разных степенях, но никто не помешает возвести это произведение тоже в куб. Далее это создаст нам некоторые затруднения, но мы как-нибудь их одолеем. И вот перед нами два уравнения:
u3v3 = - p3/27; u3 + v3 = - q.
А теперь скажите, юноша, как бы вы дальше поступили с этими уравнениями? Отвечайте, куда они просятся?
- В квадратное уравнение! - вдруг выпалил почти в отчаянии Илюша. - Сумма и произведение даны, значит, это квадратное уравнение... по теореме Виеты.
- Очень хорошо! - отозвался Мнимий. - Так вот: теперь должно быть ясно, что болонцы действительно напали на очень счастливую мысль. Разумеется, им не удалось свести кубическое уравнение к линейному (то есть первой степени), как сводили квадратное, но ведь этого и ожидать было бы странно, ибо куб все-таки постарше квадрата и, конечно, поупрямей его! Но вы должны еще иметь в виду, что открытие этого решения кубического уравнения в Италии шестнадцатого века было поистине важным историческим событием! Оно означало, что новая Европа вышла на новый рубеж, она уже освоила наследие древних ученых и теперь сама делает недоступные для древности открытия. Общественные условия настолько изменились, что возникла возможность для новой науки. Разумеется, ученый работает прежде всего в интересах науки. Но он может работать для ее развития только тогда, когда общество, в котором он живет, поддерживает его, другими словами, когда люди верят в необходимость его трудов.
Мы уже говорили с вами, как бились древние греки с двоекубием, то есть задачей удвоить куб. И как мы увидим далее, задача трисекции угла тоже сводится к кубическому уравнению. Но так или иначе болонцы все-таки степень кубического уравнения на единицу понизили, а это облегчило задачу - квадратные уравнения мы решать умеем!
- Вавилоняне догадались, - заметил Радикс, - да и нас научили.
- 434 -
- И теперь уже мы можем составить окончательное уравнение, которое будет:
t2 + qt - p3/27 = 0
Одно значение корня этого уравнения даст u3, а другое v3.
Решим это уравнение!
Илюша схватил мел и сразу написал:
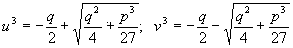
- Вот-вот, - поддакнул Мнимий, - совершенно правильно.
На пятерку! Но теперь, поскольку мы знаем, что у - и + v, пишите уж и самое решение.
И наш герой написал следующее:
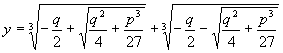
- Ну вот, - произнес Мнимий, - и появилась эта знаменитая формула Кардана для решения кубического уравнения.
- Так, - сказал Илюша, любуясь своим произведением, -< это я теперь как будто сообразил. Но при чем же тут мнимые человечки?
- А-а-а, - важно протянул Мнимий, - вот вас что интересует! Ну что же? Мы постараемся приподнять завесу этой трудной научной тайны.
- Жаль, что в науке есть еще тайны!
- Н-да... - протяпул Мнимий. - В общем, конечно, досадно. Но ведь эти тайны исходят не от науки, они, скорее, принадлежат природе. Человек начинает с самого простого, а затем идет все дальше, все время углубляет свои знания, раскрывает тайну за тайной, похищая их у Природы! И вот вы сами видите в наши дни, как увеличивается могущество человека. А те тайны науки, о которых вы сокрушаетесь, - это уж не совсем тайны, это ее трудности, но опыт показывает, что их можно одолеть. Вы могли видеть сами на примере решения кубического уравнения, как осторожное расширение способа двучленного уравнения позволяет добиться новых результатов. Трудность основная в том, что при всяком таком расширении области, где применяется данный способ, дело усложняется новыми обстоятельствами и обычно такими, которые ранее невозможно было не только предвидеть, но даже и представить себе.
- 435 -
С развитием науки приходится решать более сложные и запутанные задачи. К примеру: обычное уравнение имеет одно решение; квадратное уже дает два, причем бывает, что оба имеют смысл самый простой, а случается и другое!
А кубическое уравнение, вообще говоря, должно давать три решения, но, даже и получив все элементы, из которых легко составить эти решения, надо еще сперва сообразить, как их составлять. Мы недавно любовались на график квадратного уравнения, но ведь график кубического уравнения, то есть кубической параболы, гораздо сложнее и все случаи решения кубического уравнения много хитрее. Кубическое уравнение может иметь три действительных корня, либо один действительный и два комплексных корня. Переходя к графику, мы видим, что кубическая парабола может иметь различные формы: 1) парабола пересекает ось абсцисс однажды (все три действительных корня равны друг ДРУГУ); 2) парабола пересекает ось абсцисс однажды и однажды ее касается (три действительных корня, причем два из них равны друг другу); 3) парабола пересекает ось абсцисс трижды (три разных действительных корня); 4) парабола пересекает ось абсцисс однажды, а кроме того, у нее имеются еще два сопряженных комплексных корня.
- По-моему, я такую параболу видел, - вспомнил Илюша, - в Схолии Шестнадцатой, там еще была и такая, которая у вас здесь под номером третьим.
- Это верно, - подтвердил Радикс, - так и было.
- В этом последнем случае, значит, - продолжал Илюша, - эти комплексные корни будут: один а + bi, а другой, ему сопряженный, а - bi.
- Конечно, - подтвердил Мнимий. - Но ведь это еще отнюдь не все. Самое удивительное качество решения кубического уравнения, которое крайне поразило алгебраистов шестнадцатого века, заключается в том, что иногда попадается такое кубическое уравнение, что если мы станем решать его по Кардановой формуле, то, невзирая на то что все три корня его вещественны, формула Кардана выражает эти корни мнимыми радикалам и, и можно доказать, что ничего иного из формулы Кардана вообще получить невозможно.
То есть истинное решение словно прячется за мнимостями! Это тот случай, который Кардаи называл "неприводимым" (Кардан уже знал, что у кубического уравнения три корня). Тут болонские алгебраисты впервые убедились, что наши мнимые человечки действительно существуют, активно участвуют в алгебраических построениях и при решении самой вещественной задачи невозможно обойтись без того, чтобы с ними не встретиться. Тут надо вот что еще иметь в виду: обычные числа человек придумал для счета.
- 436 -
Всякого рода задачи, которые пришлось решать, привели неизбежно к понятию различных математических образов, которые получаются по крайней мерс; из пары чисел, как, например, сумма, разность, произведение, частное или дробь. А затем уже пошли еще более сложные построения, как и мы, мнимые человечки, которые выросли из задач, связанных с квадратным уравнением. Счет - одно, а расчет - другое! Но именно для того, чтобы наши расчеты не противоречили простому счету, чтобы правильность счета нигде и никогда не нарушалась, и приходится вводить такие сложные и хитрые построения, где из пары чисел получается одно особенное число. Но ведь зато и результаты получаются обширные и замечательные! Однако самая суть дела в том, что кубическое уравнение с его необычайными сложностями заставило математиков понять, что мы, мнимые хитроумные человечки (от которых до той поры, встречаясь с нами в квадратных уравнениях, просто отмахивались!), вовсе не случайные призраки, а самые настоящие граждане и деятели математического мира!
- Все-таки трудно... - признался Илюша.
- Разумеется, не очень просто, - согласился Мнимий. - Но вы подумайте еще о том, что в те времена все это было еще трудней, потому что нашей удобной алгебры с буквенными знаками еще не существовало. Тарталья, кстати сказать, изложил формулу Кардана в стихах, а потребовалось ему для этого двадцать пять строк!
- Ого, - отозвался Илюша, - целая поэма!
- Вот именно. И что было делать с этой формулой, как рассудить о ее странностях, долгое время не знали. Пока кубическое уравнение таково, что у него только один действительный корень, выражение под квадратным корнем
(q/2)2 + (p/3)3
больше нуля, и тогда вычисления не так трудны. Но в другом случае - и как будто в самом простом, ибо тогда все три корня действительны! - это выражение становится меньше нуля, и как быть с формулой, неясно. Только через четверть века Рафаэль Бомбелли, последователь Кардана, нашел выход из положения. Начал он, как нередко в таких случаях бывает, с частного случая, с численного примера. Он взял такое кубическое уравнение:
x3 - 15x = 4
Решить его ничего не стоит без всякой формулы... Как вы скажете?
- 437 -
Илюша в ужасе уставился на уравнение. Наконец еле выдавил из себя:
- Четыре в квадрате - шестнадцать, а здесь пятнадцать, а четыре в кубе - шестьдесят четыре... Мне кажется, что решение равно четырем, потому что:
64 - 15•4 = 64 - 60 = 4.
- Вы совершенно правы! - весело воскликнул Мнимий. - Как видите, решить совсем нетрудно. А теперь попробуйте с формулой Кардана. И тотчас получается:
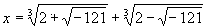
Как тут быть, неизвестно. Из ( + 121), конечно, квадратный корень извлечь небольшая хитрость, но ведь здесь минус.
Однако попробуем переписать теперь это по-нашему:
Из этого выражения Бомбелли получил (как мы теперь пишем!) такие равенства:
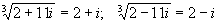
Если вы возведете каждое из этих равенств в куб, пользуясь формулой сокращенного умножения, вам хорошо известной, вы убедитесь, что равенства эти справедливы. Поскольку искомый икс равняется сумме этих двух выражений, то мы получаем...
Илюша немедленно написал ответ:
х = (2 + i) + (2 - i) = 2 + 2 = 4.