Ньютон и анализ бесконечно малых
Ньютон и анализ бесконечно малых
Исаак Ньютон — один из самых известных и уважаемых ученых всех времен. Хотя это часто не принимается во внимание, но он в наибольшей степени обязан этой славе своим способностям к математике. Именно благодаря им он заметно выделялся среди других ученых того времени, и без них было бы невозможно написание его главного труда — «Математические начала натуральной философии». Иными словами, Ньютон открыл «систему мира», благодаря чему, как удачно заметил Лагранж, стал самым удачливым из всех ученых, поскольку существует лишь одна система мира, которую можно открыть. Именно благодаря глубоким знаниям математики, которыми не обладали его современники, Ньютон смог подкрепить и обосновать свои открытия. По словам Вестфолла, «математика была первой и главной страстью Ньютона. Именно из математики он заимствовал критерии логической строгости, которых неизменно придерживался на протяжении всего своего пути в науке. Ньютон собирался совершить плавание по неизвестным океанам мысли, из которых не вернулись многие искатели приключений XVII века. Ньютон не просто вернулся из этого путешествия — он привез с собой трофеи. Возможно, именно математическая дисциплина помогла ему добиться успеха».
Многие считают, что Ньютон был исключительно физиком, точнее натурфилософом, или занимался прикладной математикой. Стоит напомнить, что писал по этому поводу Дерек Том Уайтсайд, составитель прекрасного восьмитомника рукописей Ньютона по математике: «Никогда не следует забывать, что математика была для Ньютона не просто набором инструментов для поиска истины. Она обладала внутренней красотой и силой, не зависящей от внешних причин и способов практического применения. Тем, кто не чувствует элегантность и мощь математики как самостоятельной дисциплины, я представляю Ньютона — «чистого» математика, который, как в библейской метафоре, удалился от мира в башню из слоновой кости в Кембридже, где занимался поисками новых теорем, свойств, алгоритмов и доказательств, элегантных самих по себе. И сколь удивительно он использовал свой талант и способности! В то время в мире не было более одаренного и разностороннего математика, никого, кто больше него разбирался бы в алгебре, геометрии и в тонкостях анализа бесконечно малых».
Из всех математических открытий Ньютона, вне всяких сомнений, открытие анализа бесконечно малых было наиболее важно и имело наиболее значимые последствия.
Первые идеи о математическом анализе появились у Ньютона в наиболее знаменательный период его жизни — в 1665—1666 годы. В рукописи, написанной им за несколько лет до смерти в 1727 году, мы читаем: «В начале 1665 года я открыл метод приближенного вычисления с помощью рядов, а также правило, по которому можно свести бином любой степени к такому ряду. В мае того же года я открыл метод построения касательных Грегори и де Слюза, а в ноябре получил метод флюксий. В январе следующего года я развил теорию цветов, в мае начал работать над обратным методом флюксий. В том же году я начал размышлять о тяготении применительно к орбите Луны и на основе законов Кеплера определил силы, которые удерживают планеты на орбитах».
Его первая работа по математическому анализу «Анализ с помощью уравнений с бесконечным числом членов» (De analysi per aequationes numero terminorum infinitas) была завершена в 1669 году, но опубликована только в 1711-м.
Эту книгу Ньютон написал в конце июня 1669 года (точные даты неизвестны) всего за несколько дней, взяв за основу результаты собственных исследований, проведенных в 1664 году. Ньютон использовал разложение логарифмической функции в степенной ряд, описанное Николасом Меркатором в книге Logarithmotechnia. Он также руководствовался слухами и предположениями о том, какими исследованиями в то время занимались другие ученые.

Первая страница английского издания «Анализа».
«Анализ с помощью уравнений с бесконечным числом членов» имел огромную ценность. После публикации этой работы, несмотря на ее небольшой объем, Ньютон был признан создателем анализа бесконечно малых, а его труд — основополагающим в этом новом разделе математики. В первой части книги Ньютон показывает, как с помощью степенного ряда можно произвести расчет квадратуры для множества функций, используя в качестве основы базовую квадратуру
axm/n
Рассуждения Ньютона стоит изложить подробнее. Для простоты мы приведем частный случай, описанный самим Ньютоном, для площади, ограниченной кривой, которая задается следующей формулой:
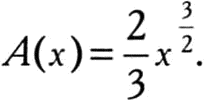
Ньютон действовал так.
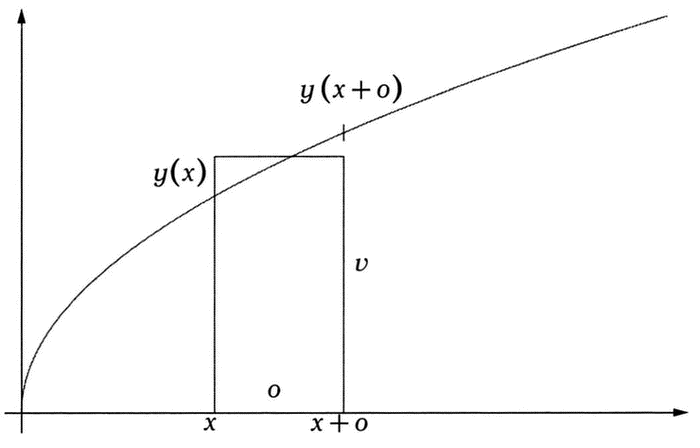
Увеличим на бесконечно малую величину, которую обозначим за о (это обозначение использовал сам Ньютон) абсциссу х. Площадь увеличится на площадь прямоугольника с вершинами x, y(x), y(x + o) и x + o, как показано на иллюстрации. Возьмем прямоугольник со сторонами o и v такой, что его площадь будет равна упомянутому приращению площади. Получим:
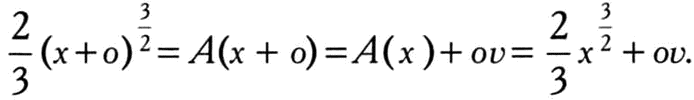
Возведя обе части в квадрат и упростив равенство, получим:
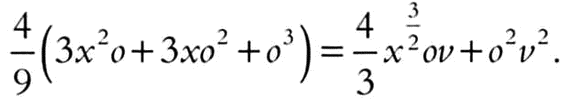
Разделив обе части на о, получим:
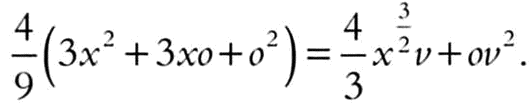
Если теперь мы примем прирост х бесконечно малым, то есть приравняем o к нулю, то v = y, и предыдущая формула примет вид
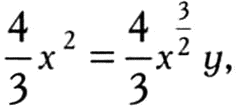
Отсюда следует, что площадь, ограниченная кривой у = х2, равна 2/3 ? 3/2 x. Может показаться, что Ньютон пытался вычислить площадь, ограниченную кривыми определенного типа, но в действительности полученный им результат намного важнее. В первой части «Анализа» Ньютон хотел изложить общий алгоритм и подчеркнуть, что он применим не только в задачах расчета площади, «Все задачи о длине кривых, о величинах и о поверхностях тел и о центрах тяжести могут быть сведены в конце концов к определению плоской поверхности, ограниченной кривой», — делает он крайне важное замечание, за которым следует раздел под названием «Приложение вышеизложенного к другим примерам того же рода». Это замечание отделяет первую часть работы, в которой изложен общий метод, от второй, в которой излагаются различные способы его применения. Можно сказать, что результат его работы несколько неопределен: Ньютон видел огромную ценность найденного им абстрактного метода, однако, возможно, на начальном этапе, когда идея еще не оформилась окончательно, ему было сложно выразить ее доступно. Скорее всего, на этом этапе ему попросту не хватало терминов и обозначений. Он сосредоточил основное внимание на абстрактной задаче определения функции по известной производной. Кроме того, он рассматривает и обратную задачу о вычислении изменения функции (об этом рассказывается в конце книги). Наконец, он приводит краткий алгоритм расчета этого изменения (производной). Четкие правила вычисления производной позднее опубликовал Лейбниц, но не будем забывать, что в «Анализе» Ньютон изложил не все результаты, полученные им в области математического анализа к 1669 году.
Всё вышеизложенное позволяет заявить, что выход «Анализа» ознаменовал появление анализа бесконечно малых. «Анализ с помощью уравнений с бесконечным числом членов» — великолепный пример, позволяющий оценить акт творения в математике во всем его великолепии: при прочтении книги Ньютона мы становимся свидетелями процесса возникновения анализа бесконечно малых. Так, если мы углубимся в чтение «Анализа» и попытаемся увидеть уже известные нам термины и понятия современного математического анализа, это можно будет сравнить с просмотром детских фотографий человека, с которым мы познакомились уже в зрелом возрасте: сквозь еще не оформившиеся, детские черты уже проступает облик знакомого нам взрослого человека.
Закончив рукопись «Анализа», который принес автору известность среди британских математиков, Ньютон показал свой труд Барроу. Тот предложил незамедлительно отправить работу Джону Коллинзу, члену Лондонского королевского общества, который занимался обработкой почты, распространением результатов и новостей подобно Марену Мерсенну. Ньютона охватил нездоровый страх, который будет сопровождать его перед публикацией всех его трудов: обнародовать труд означало подставить его под удары критиков. Здесь следует отметить, чтобы отчасти прояснить причины полемики Ньютона и Лейбница, что в те годы понятие «публикация» имело несколько иной смысл, нежели в наши дни. Сегодня это означает публикацию в научных журналах или в виде книги, доступной всем желающим. В то время, когда книги и особенно журналы еще не набрали такую популярность, как всего несколько десятилетий спустя, публикация означала представление рукописи группе близких друзей, а также тем, кто занимался распространением научных трудов, как, например, Джон Коллинз или в особенности Марен Мерсенн.
Чтобы продемонстрировать опасения Ньютона, далее мы подробно расскажем о письмах, которые Барроу отправил Коллинзу. Сначала, 20 июля 1669 года Ньютон разрешил Барроу всего лишь уведомить Коллинза, что у него находится рукопись «Анализа», запретив упоминать имя автора и название работы: «Один мой друг, обладающий блестящими способностями, отправил мне позавчера несколько писем, в которых описывает метод вычисления размерностей величин, подобный методу Меркатора, но намного более общий применительно к решению уравнений. Я отправлю вам рукопись с одним из ближайших писем и верю, что она доставит вам удовольствие».
Одиннадцать дней спустя Ньютон разрешил Барроу отправить Коллинзу копию «Анализа» при условии, что имя автора будет сохранено в тайне, а рукопись будет возвращена. Обратите внимание, как деликатно Барроу указывает, что Коллинз может ознакомиться с рукописью, но делать копию не следует, иными словами, рукопись предназначена только для Коллинза: «Отправляю вам обещанные письма моего друга, которые, как я надеюсь, доставят вам немалое удовольствие. Я прошу, чтобы вы вернули мне письма, когда сочтете нужным, после того как прочитаете их. Мой друг согласился передать мне письма только на этих условиях, когда я впервые спросил его разрешения отправить их вам. Поэтому прошу вас как можно скорее дать мне знать, что вы получили их, чтобы избавить меня от беспокойства. Чтобы вы могли как можно раньше ознакомиться с ними, я ни минуты не думал о том, чтобы послать их вам обычной почтой».
Когда Коллинз ознакомился с «Анализом» и передал восторженный отзыв Барроу, Ньютон позволил сообщить Коллинзу свое имя, а также разрешил передать рукопись другим: «Я рад, что письма моего друга доставили вам удовольствие. Имя этого юноши — Ньютон, он член нашего колледжа, обладает великолепными способностями и добился в этом вопросе потрясающих успехов. Передайте письма, если пожелаете, достопочтенному господину Броункеру». (Лорд Броункер в то время был главой Лондонского королевского общества.) Вестфолл комментирует: «Это наглядно показывает, что Ньютон, ведущий математик Европы, боялся публиковать свою работу».
ВЕРСИЯ НЬЮТОНА
Следует привести и другую версию этой истории, автором которой является сам Ньютон. Она изложена в Epistolae posterior- втором письме, которое Ньютон отправил Лейбницу. Письмо содержит немало автобиографических фрагментов. Вот цитата из него: «Когда появилась блестящая книга Logarithmotechnia Николаса Меркатора, я стал уделять этим вопросам [степенным рядам и анализу флюксий] меньше внимания, подозревая, что Меркатору был хорошо известен способ разложения в степенной ряд путем извлечения корней, равно как и разложение в ряд с помощью дробей, либо же другие обнаружат, как это делается, до того как я вступлю в возраст, достойный написания подобного труда. В тот самый момент, когда появилась эта книга, краткое изложение этого метода рядов было сообщено господином Барроу господину Коллинзу. В этом изложении указывались площади и длины кривых, поверхности и объемы тел, составленных из линий, а также способы нахождения этих линий по известным свойствам фигур. Этот метод я ранее проиллюстрировал на примере различных рядов».
Коллинз вскоре вернул рукопись «Анализа» Ньютону через Барроу, однако прежде переписал ее от руки. Эту копию вместе с письмами Барроу обнаружил Уильям Джонс среди документов Коллинза, приобретенных в 1708 году. Увидев эту копию, Джонс предложил Ньютону опубликовать «Анализ». Книга увидела свет в 1711 году. Когда же разгорелся спор о том, кто является истинным первооткрывателем анализа, эти бумаги послужили доказательством первенства Ньютона.
Как указывает Вестфолл, «Анализ» оказал большое влияние на карьеру Ньютона. Возможно, именно благодаря публикации этого труда он получил пост лукасовского профессора. Эта должность была создана в Кембридже Генри Лукасом. Стипендия, учрежденная Лукасом для тех, кто занимал эту должность, сделала ее одной из самых престижных в научном мире. В то время эта должность была единственной из восьми существовавших профессорских должностей по направлению математики и натурфилософии, если говорить современным языком. Профессор, занимавший этот пост, должен был вести курсы по геометрии, астрономии, географии, оптике, статике и другим математическим дисциплинам, а также ежегодно передавать в университетскую библиотеку тексты минимум десяти своих докладов. При невыполнении этих условий полагался штраф. Однако Ньютон, который нарушал их достаточно часто, по-видимому, никогда не был оштрафован.
Летом 1669 года Барроу, занимавший этот пост уже пять лет с момента его учреждения, начал подумывать об отставке. Скорее всего, он не был очарован гениальностью Ньютона (хотя иногда утверждают обратное), его решение было продиктовано другими причинами. Барроу был не только математиком, но и богословом и хотел последовать своему призванию. Кроме этого, он также хотел получить более влиятельный пост. Спустя год после отставки он получил место капеллана, а два года спустя возглавил Тринити-колледж. Совмещать должность главы колледжа и лукасовского профессора запрещалось, хотя Барроу вполне мог получить разрешение милостью короля. Как бы то ни было, Барроу ушел в отставку, и 29 октября 1669 года по его предложению Ньютон был провозглашен лукасовским профессором.
Остаток 1669 года Коллинз и Барроу занимались тем, что уговаривали Ньютона опубликовать «Анализ». Однако они не преуспели в этом, и, как пишет Вестфолл, имея в виду спор с Лейбницем, «нерешительность Ньютона посеяла зерна ожесточенной вражды».
Вторая работа Ньютона, его главный труд о бесконечно малых «Метод флюксий» (De methodis serierum et fluxionum), была написана два года спустя, но опубликована лишь в 1736 году. В этой книге Ньютон представляет понятие флюенты — величины, изменяющейся в зависимости от времени, и флюксии флюента — производной этой величины по времени. Вот что он пишет об этих понятиях: «Величины, которые я рассматриваю как постепенно и неопределенно возрастающие; обозначать я их буду последними буквами алфавита: v, х, у, z, чтобы их было возможно отличать от других величин, которые рассматриваются в уравнениях как известные и определенные и которые поэтому обозначаются первыми буквами алфавита a, b, c и так далее. Скорости, с которыми возрастают вследствие порождающего их движения отдельные флюэнты (и которые я называю флюксиями, или просто скоростями, или быстротами), я буду обозначать теми же буквами, но пунктированными:
Важно отметить, что Ньютон представил понятия флюенты и флюксии по отдельности как часть теории и привел алгоритмические правила, с помощью которых можно было легко вычислить флюксию флюента. Затем он применил свою теорию для решения задач о касательных, квадратурах, максимумах и минимумах. Как мы уже упоминали, именно благодаря этому Ньютон стал считаться одним из создателей математического анализа. Так, для решения задач о максимумах и минимумах он предложил следующий способ: «Когда величина есть возможно наибольшая или возможно наименьшая, то в этот момент времени она не течет ни вперед, ни назад. Действительно, если бы она могла еще течь вперед, то есть возрастать, то это значит, что до того она наверняка была меньше, чем стала, а после того станет больше, чем она есть. Дело обстояло бы обратным образом, если бы она текла назад или убывала. Поэтому найди ее флюксию согласно проблеме I и положи ее равной нулю». Это знакомый нам способ вычисления производной функции и приравнивания ее к нулю.
О задачах расчета квадратуры он писал: «Проблема IX: определить площадь какой-либо заданной кривой. Решение этой проблемы зависит от определения отношения флюент по заданному отношению флюксий». Иными словами, речь идет о процессе, обратном вычислению флюксии; если говорить современным языком — о процессе, обратном вычислению производной, то есть о нахождении первообразной. Здесь Ньютон, по сути, излагает основную теорему анализа и указывает, что ее можно применять для решения задач о площадях.
Чтобы доказать мощь своего анализа бесконечно малых, в «Методе» Ньютон использует его для решения практически всех задач о площадях, касательных и многих других, на решение которых его предшественники потратили без малого столетие. Однако «Метод» был опубликован лишь спустя несколько лет после смерти Ньютона.
Почему он так долго не давал разрешение на публикацию своих первых книг об анализе бесконечно малых? Мы уже упоминали, что Ньютон не желал публиковать свои результаты из-за особенностей своего характера. В итоге это спровоцировало ожесточенные споры, которых можно было бы избежать, если бы его первые труды были опубликованы без промедления. Нежелание Ньютона публиковать свои работы о математическом анализе было сильно еще и потому, что он осознавал его недостаточную логическую строгость. Понятие флюксии и правила ее вычисления, равно как и дифференциал Лейбница или многочисленные методы работы с бесконечно малыми, предложенные его предшественниками, основывались на так называемых бесконечно малых величинах. Эти «бесконечно малые» представляли собой бесконечно малые числа, практически равные нулю, за счет чего их можно было сокращать при необходимости. В то же время эти величины можно было использовать в знаменателях дробей, так как они не были строго равны нулю. Ньютон безуспешно пытался избежать их и в одной из работ по анализу, «Рассуждении о квадратуре кривых» (De quadratura curvarum), опубликованной в 1704 году как приложение к его же «Оптике», он вплотную подошел к открытию предела, использовав «исчезающие приращения». Это понятие было введено лишь в XIX веке, и Бернард Больцано и Огюстен Луи Коши использовали его как основу анализа бесконечно малых.
Литографический портрет Огюстена Луи Коши, одного из самых плодовитых математиков всех времен.
Ньютон осознавал, что его вычисление флюксий стоит на непрочном логическом фундаменте, поэтому особенно противился публикации любых трудов по этой теме, хотя копии этих рукописей всегда были доступны кругу его друзей. Этот страх, несомненно, оказал влияние и на подготовку его важнейшей работы — «Начал». Ньютон сделал выбор в пользу геометрического языка в древнегреческом стиле, который был менее понятным, но более строгим с логической точки зрения. Он исключил почти все упоминания об анализе бесконечно малых, который, возможно, использовал для получения части результатов, изложенных в «Началах».
Тем не менее в «Началах» содержатся отрывочные упоминания о математическом анализе. Таким образом, в этой книге впервые, пусть и косвенно, упоминается анализ бесконечно малых, созданный Ньютоном. Это произошло в 1687 году — спустя три года после того, как Лейбниц опубликовал в журнале Acta eruditorum свою первую статью о дифференциальном исчислении. В лемме II раздела II 2-й книги несколько туманно упоминаются правила, аналогичные современным правилам вычисления производной произведений и степеней. Ньютон применил математический трюк, чтобы избежать сокращения приращений. Этот трюк в середине XVIII века разоблачил Джордж Беркли, который возглавил «крестовый поход» против бесконечно малых. «Начала» вошли в историю математического анализа не только благодаря этой лемме. К математическому анализу можно отнести и другие утверждения, о которых мы расскажем чуть позже, когда будем говорить об ожесточенном споре между Ньютоном и Лейбницем за право называться создателем исчисления.
ПРОИЗВОДНАЯ ПО НЬЮТОНУ
В «Началах» Ньютон приводит следующее доказательство правила нахождения производной произведения функций: «Любой прямоугольник, например АВ, увеличенный на непрерывную флюенту, если вычесть из сторон А и В половины их моментов а и b [под моментами понимаются приращения], будет равен:
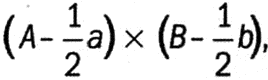
или
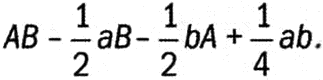
Поскольку стороны А и В увеличиваются на другую половину моментов, прямоугольник превратится в:
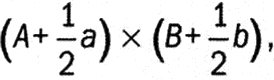
или
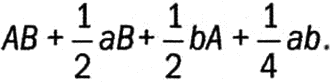
Вычтем из этого прямоугольника предыдущий прямоугольник и получим излишек aВ + bА. Следовательно, приращение aВ + bА прямоугольника генерируется общими приращениями сторон а и b. Что и требовалось доказать». Если мы запишем приращение А как dА, а приращение В — как dB (Ньютон решительно воспротивился бы использованию подобных обозначений, так как их использовал его противник Лейбниц), то получим знакомое нам правило вычисления производной произведения: d(АВ) = AdB + BdA.
Мы уже упоминали, что Ньютон ссылался на открытую им в самый знаменательный период его жизни теорему о биноме, то есть о разложении (1 + x)m/n в степенной ряд. Однако она стала достоянием общественности лишь десять лет спустя, в 1676 году, причем в сокращенном виде. Ньютон упомянул о ней в первом из двух писем, отправленных Лейбницу через секретаря Лондонского королевского общества Генри Ольденбурга. В этом письме, озаглавленном Epistolae prior, Ньютон, отвечая на вопросы Лейбница, изложил свою теорему о биноме и другие результаты, касающиеся рядов.
Теорема о биноме легла в основу созданного им анализа бесконечно малых. По сути, именно с помощью бинома Ньютон разложил в ряд большинство элементарных функций: обратных тригонометрических (их производные можно найти с помощью бинома), а на их основе и тригонометрических функций. Аналогично он вычислил производные логарифмических и показательных функций.
Некоторые из полученных результатов уже были известны. Разложение в ряд для логарифмической функции впервые приводится в уже упоминавшейся книге Николаса Меркатора Logarithmotechnia (1668).
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
Глава 3 Анализ
Глава 3 Анализ А что такое эти флюксии? Скорости исчезающих приращений. А что такое эти самые исчезающие приращения? Они не есть ни конечные величины, ни величины бесконечно малые, но они и не нули. Разве мы не имеем права назвать их призраками исчезнувших величин? Епископ
Глава 5. Анализ данных
Глава 5. Анализ данных Руководство крупной американской сети супермаркетов Osco несколько лет назад поставило перед службой информационных технологий задачу разработать систему, способную анализировать огромные объемы данных, генерируемых ежедневно.Предполагалось,
Анализ периодичности кометы Галлея. Список дат её появления
Анализ периодичности кометы Галлея. Список дат её появления Начнем со списка дат, обычно считающихся датами появления кометы Галлея. Список разбивается обычно на две части: китайские записи о комете Галлея и европейские. Приведем оба списка в сравнении друг с
Глава 1. Что такое анализ бесконечно малых и для чего он нужен
Глава 1. Что такое анализ бесконечно малых и для чего он нужен Анализ бесконечно малых — это область математики, которая имеет огромное значение для науки и техники. Чтобы понять, из чего состоит эта сложная и тонкая дисциплина, наверное, следует начать с рассказа о
Глава 3. Ньютон, последний из волшебников
Глава 3. Ньютон, последний из волшебников День 13 июля 1936 года стал поворотным в изучении биографии Исаака Ньютона и его наследия. В этот и последующий день на аукционе «Сотбис» было продано 332 лота: рукописи, письма и другие документы, принадлежавшие Ньютону. Запутанная
Ньютон и его друзья
Ньютон и его друзья Портрет Ньютона будет неполным, если мы не упомянем о его отношениях с друзьями и близкими.Быть может, причиной тому, что Ньютон тяжело сходился с людьми, был его непростой характер. Правда, в последние годы, прожитые в Лондоне, он пользовался славой
Лейбниц и анализ бесконечно малых
Лейбниц и анализ бесконечно малых «Почти все остальные крупные математики, — писал в XX веке Иозеф Хоффман, видный исследователь биографии Лейбница, — увлекались математикой уже в юные годы и разрабатывали радикально новые идеи. Однако этот период в жизни Лейбница не был
Ньютон, Лейбниц и бесконечно малые
Ньютон, Лейбниц и бесконечно малые Даже создатели математического анализа не приводили исчерпывающих доказательств открытых ими методов. И Ньютон, и Лейбниц осознавали недостаток логики в своих работах и пытались каждый по-своему если не устранить, то хотя бы смягчить
Эйлер и анализ бесконечно малых
Эйлер и анализ бесконечно малых Если Ньютон и Лейбниц считаются создателями дифференциального и интегрального исчисления, то Эйлера можно назвать создателем математического анализа — области математики, куда входят оба эти раздела. В этом смысле его книги «Введение в