Лейбниц и анализ бесконечно малых

Лейбниц и анализ бесконечно малых

«Почти все остальные крупные математики, — писал в XX веке Иозеф Хоффман, видный исследователь биографии Лейбница, — увлекались математикой уже в юные годы и разрабатывали радикально новые идеи. Однако этот период в жизни Лейбница не был ознаменован какими-либо заметными математическими открытиями». И в этом, и во многом другом Лейбниц очень отличается от Ньютона.

Когда Лейбниц прибыл в Париж, ему было уже 26 лет. К этому времени он был лишь поверхностно знаком с «Началами» Евклида и знал немногим больше элементарной арифметики, изученной в школе по книге Клавия. Как рассказывал много лет спустя один из его первых учеников Иоганн Бернулли, издание «Геометрии» Декарта с комментариями Ван Схотена, с которым Лейбниц бегло ознакомился в университете, показалось ему слишком сложным. В Нюрнберге, где он жил после получения степени доктора в Альдорфском университете (1666 год), он поверхностно изучил Geometria indivisibilibus Кавальери. Так что, когда он прибыл в Париж в марте 1672 года, его знания были весьма плачевными, хотя, по словам Хоффмана, математика была у Лейбница в крови.

Сохранилось множество рукописей и документов Лейбница, в частности почти все, написанное им в период обучения в Париже. Эти документы позволяют понять, как проходило его обучение и как он пришел к открытию анализа бесконечно малых.

В первый год в Париже Лейбниц был дилетантом в математике. Позднее он сам признавался, что мучился от недостатка знаний. В этом же году он впервые побывал в Лондоне, где при посредничестве Ольденбурга и Коллинза познакомился с английскими математиками. Его «святая простота», о которой он знал, его недооценка собственных возможностей вкупе с излишней открытостью и общительностью не раз приводили к недопониманию с британскими математиками и впоследствии стали одной из причин обвинений в плагиате.

Осенью 1672 года он познакомился с Христианом Гюйгенсом, самым известным ученым и математиком Европы, который в то время получал жалование во Французской академии наук. К тому времени Лейбниц уже совершил свое первое математическое открытие: он показал, как использовать разность для сложения чисел. Позднее он упоминал, что на мысль о взаимно обратной связи дифференцирования и интегрирования его навела взаимно обратная связь между сложением и вычитанием.

Рассуждения Лейбница были таковы. Допустим, что требуется найти сумму а_{1 +} а₂ + а₃ + … + а_n. Нам известно, что каждое из этих чисел является разностью двух других: a_k = b_k+1 — b_k. Следовательно, простое сокращение последовательных членов b_k означает, что а_{1 +} а₂ + а₃ + … + а_n = b_n+1 — b₁.

Ввиду врожденного оптимизма и недостатка математических знаний Лейбниц посчитал, что открыл способ нахождения суммы произвольных рядов чисел. Его уверенность только усилилась, когда он поделился своим открытием с Гюйгенсом и тот предложил найти сумму чисел, обратных треугольным числам:

¹/₂ + ¹/₆ + ¹/₁₂ + ¹/₂₀ + …

По случайному совпадению, этот ряд — один из немногих, к которым применим способ, открытый Лейбницем, так как члены этого ряда имеют вид ¹/_n(n+1), то есть равны разности между ¹/_n и ¹/_(n+1). Таким образом,

¹/₂ + ¹/₆ + ¹/₁₂ + ¹/₂₀ + … = 1

Лейбниц вычислил суммы похожих рядов, образованных пирамидальными числами, и подготовил небольшую статью для публикации в Journal des Savants. Однако статья так и не увидела свет, поскольку весь 1673 год журнал не издавался. В этой статье Лейбниц цитирует Кавальери, Галилея, Валлиса, Грегори, Паскаля, Сен-Венсана и Архимеда, а также упоминает Гоббса как великого математика, что указывает на определенный прогресс в его образовании.

В январе 1673 года Лейбниц впервые посещает Лондон. Свой первый визит он нанес Генри Ольденбургу, секретарю Лондонского королевского общества и своему соотечественнику, который принял его с распростертыми объятиями.

ГЕНРИ ОЛЬДЕНБУРГ (1618-1677)

Ольденбург родился в немецком городе Бремене. О его юности известно очень немногое. Примерно в 1654 году он был уполномочен властями Бремена на выполнение дипломатической миссии в Англии, где в то время правил Оливер Кромвель. С 1654 по 1661 год, когда он был избран членом Лондонского королевского общества, он с перерывами находился в Англии, Ольденбург упоминается как один из секретарей Королевского общества в двух первых письмах короля, датированных 1662 и 1663 годом. Этот пост он занимал в течение 15 лет, вплоть до своей смерти в 1677 году. Он создал полноценную систему архивов и поддерживал переписку со многими учеными Англии и других стран, что позволило ему осуществлять важнейший обмен идеями. Именно через него проходили письма, которыми обменивались Ньютон и Лейбниц в 1676-1677 годах. Их переписка прекратилась со смертью Ольденбурга. Не забывайте, насколько сложным в те годы было поддержание подобных связей: почта в то время где-то не существовала вовсе, где-то работала крайне ненадежно, особенно при передаче писем между странами, находящимися в состоянии войны. Используя дипломатические каналы, Ольденбург создал сеть посредников, которые передавали корреспонденцию, что было особенно ценно во время войны. Подобный шаг был достаточно рискованным: в 1667 году Ольденбург провел несколько месяцев в лондонском Тауэре, возможно, из-за того, что позволил себе «недостаточно патриотичные высказывания» о британских властях в письме к иностранцу.

22 января 1673 года Лейбниц представил Лондонскому королевскому обществу деревянную модель вычислительной машины, способной выполнять сложение, вычитание, умножение и деление. Хотя модель, изготовленная в Париже, была несовершенной, именно за ее создание Лейбниц впоследствии был избран членом Королевского общества. Ольденбург сообщил ему об этом в письме, написанном в апреле того же года, однако два месяца спустя напомнил, что он обещал представить членам общества усовершенствованную модель. Свое обещание Лейбниц выполнил лишь несколько лет спустя.

^{Лейбниц создал машину, способную умножать числа путем многократного выполнения сложения.}

Некоторое время спустя между Лейбницем и Джоном Пеллом произошел инцидент, в котором англичане встали на сторону Пелла. Лейбниц познакомился с Пеллом на встрече с Робертом Бойлем в доме его сестры на улице Пэлл-Мэлл. Как позднее вспоминал Лейбниц, он иногда посещал Бойля, так как «не пренебрегал химией». Лейбниц сообщил Пеллу, что открыл общий метод представления и интерполяции рядов с помощью разностей чисел. Пелл был удивлен: Лейбниц приехал из Парижа и должен был знать, что эти результаты уже были опубликованы во Франции и в Англии несколько лет назад Габриелем Мутоном. Лейбниц на следующий же день ознакомился с книгой Мутона в библиотеке Королевского общества и убедился, что Пелл был совершенно прав. Версия Лейбница была зафиксирована в письме к Ольденбургу от 3 февраля 1673 года, а тот в свою очередь сообщил об этом Ньютону. В итоге спустя 14 лет, когда возник спор о том, кто же первым открыл анализ бесконечно малых, Ньютон, словно желая показать склонность Лейбница к плагиату, писал: «Пелл обвинил Лейбница в том, что тот скопировал метод интерполяции из книги Мутона».

В последующие месяцы Ольденбург и Лейбниц обменялись письмами, в которых последний пожаловался на недостаток знаний математики. Как позднее вспоминал Лейбниц, в то время он совершенно не знал геометрии. Например, в апреле

1673 года Лейбниц написал Ольденбургу о результатах, касавшихся сумм чисел, обратных фигурным числам. (Ньютон позднее высмеивал эти результаты, так как они были очень простыми.) Когда Ольденбург сообщил, что эти результаты содержатся в книге Quadrature arithmeticae Пьетро Менголи, Лейбниц ошибочно возразил ему, что метод Менголи применим только для конечных, а не для бесконечных рядов. Изучив подробнее труд Менголи, Лейбниц увидел различие между своими результатами и результатами Менголи: они были получены с помощью разных методов.

Ольденбург также выслал Лейбницу результаты, которые Коллинз считал наиболее показательными для британской математики того времени. Эти результаты приводились без доказательств, иногда их было сложно понять, кроме того, при переписывании были допущены ошибки. Так как переписка часто сохранялась в архивах Лондонского королевского общества, целью этих писем было документально зафиксировать первенство английских математиков. Ньютон подробнейшим образом изучил эти письма, чтобы подкрепить обвинения Лейбница в плагиате, хотя Ольденбург отправил Лейбницу не письма Коллинза, а их сокращенный перевод с английского на латынь. Из-за этих сокращений вкупе с ошибками, допущенными при переписывании, письма Ольденбурга было практически невозможно понять.

Лейбниц, получив эти письма, решил, что ему следует уделять больше времени и внимания математике и завершить свое образование. Именно тогда его охватила подлинная страсть к математике. Он более чем на год прервал переписку с Ольденбургом и принялся за работу. По словами Хоффмана, «он прекратил отношения с Ольденбургом, чтобы заняться самообразованием и заполнить пробелы в знаниях, которые он с болью осознавал. Их отношения возобновились лишь в конце лета 1674 года. Тогда Лейбниц был уже другим человеком и превосходно разбирался в предмете».

Лейбниц позднее писал, что обширным знаниям математики он был обязан наставничеству и примеру Гюйгенса. Следуя советам этого голландского ученого, который в то время благосклонно относился к нему, Лейбниц изучил труды Паскаля, Фабри, Грегори, Сен-Венсана, Декарта и де Слюза, а также Меркатора, книгу которого, Logarithmotechnia, он купил в Лондоне, равно как и Lectiones Барроу. Однако эти работы он изучил лишь несколько лет спустя. С книгами остальных авторов он ознакомился в королевской библиотеке, некоторые приобрел. Одной из таких книг было издание «Геометрии» Декарта под редакцией ван Схотена, которое в период жизни в Нюрнберге показалось Лейбницу слишком сложным. Особенно важным стал труд Паскаля Traite des sinus du quart de cercle, в котором рассказывалось о так называемом характеристическом треугольнике — прямоугольном треугольнике, гипотенуза которого является касательной к кривой, а катеты — дифференциалами x и у, как показано на рисунке.

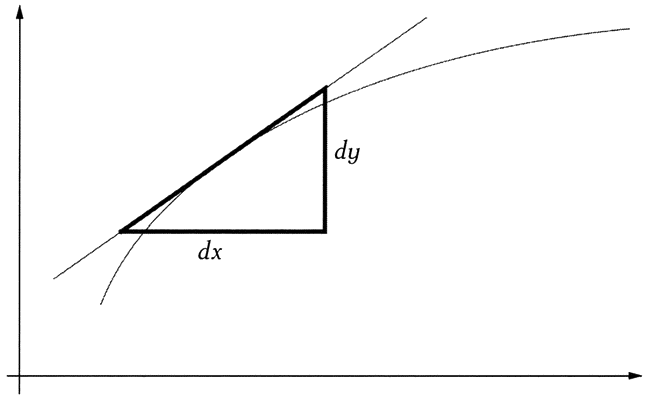
Несколько лет спустя в письме к одному из своих первых учеников Якобу Бернулли Лейбниц написал, что именно эта работа Паскаля со всей ясностью показала ему, что задачи о касательных и квадратурах являются взаимно обратными. Лейбниц добавил, что у Паскаля, должно быть, была повязка на глазах — ничем иным нельзя объяснить то, что он сам не заметил этого. Лейбниц продемонстрировал племяннику Паскаля свою вычислительную машину в июне 1674 года. Паскаль также придумал вычислительную машину, которая, однако, была способна выполнять только сложение и вычитание. Лейбниц выразил сожаление, что некоторые статьи Паскаля были до сих пор не опубликованы, и попросил его племянника отправить ему несколько рукописей этого французского математика и философа.

В течение 1673 года Лейбниц с помощью характеристического треугольника совершил несколько важных открытий. В частности, он открыл метод преобразования, напоминающий современный метод интегрирования по частям. Взяв за основу этот метод, он смог найти разложение в ряд для функции арктангенса и получил свой знаменитый бесконечный ряд, с помощью которого можно вычислить число 71. В декабре 1673 года Лейбниц обсудил с Гюйгенсом возможность решения классической греческой задачи о квадратуре круга с помощью этого ряда.

Далее он занялся решением задач о касательных, взяв за основу метод де Слюза. Хоффман, подробно изучив рукописи Лейбница того периода, сделал вывод, что в своей работе Лейбниц опирался на труды вышеупомянутых авторов, к которым следует добавить Гюйгенса, и не использовал работы Ньютона и Барроу.

В письмах, отправленных во второй половине 1674-го и в начале 1675 года, Лейбниц сообщил Ольденбургу о своих результатах, полученных, по его словам, отчасти «благодаря редкой удаче». В частности, он ознакомил Ольденбурга (не приведя ни подробностей, ни формулы) с рядом для вычисления числа 71, разложением функции арксинуса в ряд, а также косвенно упомянул метод преобразования. На этот раз Ольденбург ответил ему в более критическом тоне, чем в ранний период их знакомства, так как в то время Лейбниц не скрывал своего дилетантства. Также не приводя ни подробностей, ни формул, он сообщил Лейбницу о результатах, полученных британскими математиками, в частности Ньютоном и Джеймсом Грегори: «Мне хотелось бы обратить ваше внимание на то, что теория и метод измерения кривых, которые использует уже упомянутый Джеймс Грегори, а также Исаак Ньютон, могут быть применены к любой кривой, механической или геометрической». В письме от 20 марта 1675 года Лейбниц просит подробнее рассказать об этих результатах.

Ольденбург переадресовал письмо Коллинзу, после чего 12 апреля направил Лейбницу ответ, в котором указывается разложение в ряд для синуса и арксинуса, полученное Ньютоном, ряды Грегори для тангенса и арктангенса, а также некоторые результаты, касающиеся интерполяции, квадратур и других задач. Как бы то ни было, в письме приводились лишь результаты, но не объяснялось, каким способом они были получены. Лейбниц приписал авторство этих рядов Ольденбургу и, по мнению Хоффмана, не совсем понял, что попало ему в руки, так как пообещал сравнить эти результаты со своими и дать по этому поводу комментарий, но так никогда и не сделал этого. Так как о некоторых из этих рядов Лейбниц узнал позднее и из других источников, это дало Ньютону основания впоследствии обвинить его в плагиате результатов, полученных через Ольденбурга.

Мы можем достаточно точно указать, когда Лейбниц открыл анализ бесконечно малых. Это произошло в конце октября — начале ноября 1675 года, если вообще уместно приводить столь точные даты для такого значимого открытия. В сохранившихся рукописях, которые относятся к этому периоду, особенно тех, что датированы 29 октября и 11 ноября, Лейбниц вводит систему обозначений математического анализа и описывает с ее помощью алгоритм, в котором впоследствии станут заметны различия с работами его предшественников, приводит правила анализа и определяет интегрирование и дифференцирование как взаимно обратные операции. Хоффман пишет: «После того как был сделан этот первый, решающий шаг в сторону «алгебраизации» задач о бесконечно малых, перед этим человеком, умевшим определить характерные и общие элементы среди мешанины похожего, открылась новая картина мира. <…> Он четко понимал, чего не хватает в созданном им математическом анализе, но знал, что эти недостатки можно исправить и что путь в новый мир успешно открыт».

Ключевую роль сыграли работы по решению задач поиска кривой по заданной касательной, которыми Лейбниц занимался в октябре 1675 года. За год до этого он решил задачу определения кривой по известной поднормали.

В рукописи, датируемой 29 октября 1675 года, Лейбниц ввел знак ? — стилизованную букву S, первую букву латинского слова summa для обозначения суммы бесконечно малых. До этого использовалась аббревиатура omn. — от латинского de omnium («все»), введенная Кавальери. Лейбниц писал: «Будет удобно записывать omn. как ?, так что ?l = omn.l, то есть сумма l».

Далее в этой же рукописи он вводит букву d для обозначения дифференциала.

Изначально он поместил это обозначение в знаменатель: «Это получается обратным расчетом. То есть допустим, что ?l = уа, где l = ya/d. Тогда с ростом ?d будет уменьшаться в размерах. Однако ? означает сумму, a d — разность».

Спустя несколько дней в рукописи, датированной 11 ноября 1675 года, он переместил d в числитель и записал — как dx. В этой же рукописи Лейбниц задается вопросом о равенстве d(xy) и dxdy, а также

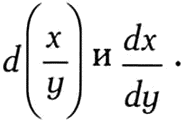
Он делает вывод, что равенство между ними не выполняется, однако не приводит верных формул для нахождения дифференциала произведения и частного.

Чтобы увидеть нечто общее среди беспорядочного множества результатов, полученных его предшественниками при решении задач о квадратурах, центрах тяжести, касательных, задач нахождения кривой по заданной касательной и других, и сформулировать понятия интегрирования и дифференцирования, требовался алгебраический язык. Этот язык Лейбниц в совершенстве освоил во время работы над решением уравнений, проведенной за несколько месяцев вплоть до октября 1675 года. Следует отметить, что Лейбниц не преуспел в решении уравнений, однако освоил язык алгебры, без которого не смог бы впоследствии открыть свой метод математического анализа.

^{Дом, в котором жил Лейбниц во время пребывания в Ганновере.}

Лейбниц сообщил основу своего метода Ньютону в ответ на его письма, переданные через Ольденбурга в июне и октябре 1676 года. Эта переписка Ньютона и Лейбница впоследствии сыграла решающую роль в споре о том, кто же первым создал анализ бесконечно малых. Как мы уже говорили, Ньютон отправил Лейбницу два письма: так называемое Epistolae prior, датированное 13 июня 1676 года, и Espistolae posterior, датированное 24 октября 1676 года. Ответы Лейбница датируются 17 августа 1676 года и 11—12 июня 1677 года. Они не озаглавлены, но их значение не менее масштабно. В своих письмах Ньютон излагает Лейбницу большую часть De analysi и De methodis о разложении в ряд, но почти не упоминает о своей версии анализа бесконечно малых. Лейбниц же в своих письмах излагает свой метод полностью. Ньютону следовало понять, что метод Лейбница столь же полон, как и его собственный, и вовремя опубликовать свои труды, чтобы доказать свое первенство. Вестфолл пишет: «Можно лишь предполагать, каковы были бы возможные последствия этого шага, но можно с уверенностью сказать, что в этом случае обе стороны не запятнали бы себя позорными поступками, которые в итоге совершили». Валлис чрезвычайно проницательно заметил: «По моему мнению, господину Ньютону следует усовершенствовать свою нотацию и незамедлительно опубликовать эти письма [имеются в виду два Epistolae]».

Годы, проведенные в Париже, стали для Лейбница непростыми. После смерти курфюрста Майнца в феврале 1673 года и изменений в ходе военных действий между Францией и Голландией политическая и дипломатическая миссия Лейбница потеряла смысл. Лейбниц опасался, что ему прикажут вернуться в Германию. Однако его новый покровитель предложил ему остаться в Париже и продолжать работу.

Лейбниц предпринял несколько неудачных попыток получить должность во французской столице. Ему не удалось получить пост дипломата (этому помешало его происхождение), а также не удалось занять оплачиваемый пост во Французской академии наук, где он представил свою вычислительную машину в начале 1675 года. (К сожалению для него, оплачиваемые должности уже занимали Гюйгенс и Кассини, и Академия не могла принять еще одного иностранца.) Несмотря на то что Лейбниц в течение всей второй половины того года использовал все свои многочисленные связи, попытка получить должность заведующего кафедрой в Коллеж де Франс после смерти Роберваля также окончилась неудачей. Шло время, но единственное предложение, которое ему поступило, — это приглашение на службу к графу Иоганну Фридриху, курфюрсту Ганновера. Лейбниц в конце концов принял предложение, но это означало, что ему придется вернуться в Ганновер, жить вдали от главных научных центров того времени и полностью зависеть от курфюрста, рискуя потерять должность в любой момент. Ему удалось продлить свое пребывание в Париже, насколько это было возможно — сначала до мая 1676 года, затем до октября. 4 октября он оставил Париж и направился в Германию, где его ждала должность библиотекаря в Ганновере. К работе следовало приступить в январе. Он больше никогда не возвращался в город, где в условиях величайшего давления, обеспокоенный будущей карьерой, он открыл анализ бесконечно малых.

По пути в Ганновер Лейбниц посетил Лондон и Амстердам. В Лондоне он пробыл десять дней и нанес визит Коллинзу. Вестфолл пишет: «Находясь под впечатлением от визитера, Коллинз открыл перед ним свой архив». Лейбниц, помимо прочих трудов, ознакомился с «Анализом» Ньютона и сделал некоторые пометки, касавшиеся разложения в ряд. Вновь приведем цитату Вестфолла: «Он увидел, что в этой области он может многому научиться у британских математиков. Отсутствие пометок, касающихся анализа флюксий, означает, что он не увидел в книге Ньютона ничего такого, о чем не знал бы сам. После отъезда Лейбница Коллинз вернулся к реальности и осознал, насколько опрометчиво поступил. Он никогда не рассказывал Ньютону о том, что показал Лейбницу его труды… Лейбниц, в свою очередь, также предпочел не упоминать об этом».

Позднее Лейбниц предпочел умолчать не только об этом, но и о других вещах, которые он узнал по дороге в Германию. В Амстердаме он в течение месяца несколько раз встретился с философом Бенедиктом Спинозой и ознакомился с частью рукописи его «Этики». Позднее Лейбниц отрицал идеи Спинозы (на момент визита Спинозе, которому оставался всего год до смерти, наскучило всякое общество) и предпочел не упоминать о том, как много он узнал во время бесед с ним, и также отказывался признавать значительное влияние «Этики» на свои философские взгляды.

Когда 25 лет спустя начался спор о том, кто же первым открыл математический анализ, решающую роль сыграло то, что Лейбниц увидел в Лондоне.

^{Портрет Бенедикта Спинозы. Доктрина этого философа, жившего в изгнании, оказала огромное влияние на многих философов, среди которых был и Лейбниц.}

В 1677 году, уже будучи в Ганновере, Лейбниц получил правильные формулы для вычисления дифференциала произведений, дробей и степеней. Эти формулы он вывел не без труда, путем проб и ошибок.

В 1680 году он практически завершил работу над своим методом анализа и, в отличие от Ньютона, который не горел желанием отдавать рукописи в печать, опубликовал первую статью по этой теме в 1684 году. Эта статья стала первой в истории публикацией, посвященной анализу бесконечно малых. Она имела внушительное заглавие «Новый метод максимумов и минимумов, а также касательных, для которого не являются препятствием ни дробные, ни иррациональные величины, и особый для этого род исчисления». В этой статье объемом всего в шесть страниц крайне схематично, без доказательств и практически без примеров было изложено дифференциальное исчисление Лейбница. Эта работа была сложной и непонятной, «скорее, загадка, нежели объяснение», как отзывались о ней братья Бернулли, которые первыми изучили математический анализ Лейбница. Сложность статьи усугублялась опечатками, допущенными при публикации.

Особого упоминания заслуживает один из немногих примеров, приведенных в статье, которому Лейбниц посвятил заключительные строки. Речь идет о задаче нахождения кривой по известной касательной, предложенной де Боном: «Я с удовольствием приведу в качестве приложения решение задачи, предложенной де Боном, которую безуспешно пытался решить Декарт. Найти линию такой природы, что проекция любой из ее точек на ось и точка пересечения касательной в этой точке с указанной осью образуют отрезок постоянной длины». Чтобы найти решение с помощью своего метода и тем самым доказать его возможности, Лейбницу понадобилось всего полдюжины строк. Искомой кривой в этой задаче является логарифмическая кривая.

Также следует обратить внимание, насколько своеобразным способом Лейбниц распространял информацию о своем дифференциальном исчислении. Он опубликовал свою работу в научном журнале Acta eruditorum, в создании которого участвовал в 1682 году, ознаменовав тем самым начало новой эпохи в науке.

ПРОБЕЛЫ В РАССУЖДЕНИЯХ ГЕНИЯ

Приведем вывод формулы производной произведения функций, изложенный Лейбницем, так как в нем ярко отражена недостаточная логическая строгость, которой отличался Лейбниц при работе с бесконечно малыми величинами: «d(xy) — то же, что и разность между двумя смежными xy, из которых одним будет xy, другим — (x + dx) (у + dy). Следовательно, d(xy) — (x + dx) (у + dy) — xy, или xdy + ydx + dxdy, что равно xdy + ydx, если опустить величину dxdy, которая является бесконечно малой по отношению к прочим величинам, так как dx и dy предполагаются бесконечно малыми».

Как видите, четкость этого доказательства оставляет желать лучшего. В нем проявляется наиболее противоречивое свойство бесконечно малых величин: Лейбниц считает величину dxdy равной нулю, несмотря на то что ни dx, ни dy не равны нулю.

Спустя два года, в 1686 году, Лейбниц публикует в Acta eruditorum свою вторую статью, которая на этот раз посвящена интегральному исчислению. Статья носила название «О скрытой геометрии и анализе неделимых и бесконечных величин». Лейбниц начал эту статью с оправданий, объясняя, почему его первая статья была столь сложной: «Понимая, что некоторые вещи, опубликованные мной в Acta об открытиях в геометрии, не были в достаточной мере поняты некоторыми учеными людьми и, более того, использованы не совсем верно, будь то по ошибке либо по какой-либо другой причине, я посчитал, что крайне ценно добавить к этой статье все возможное, чтобы прояснить прошлые вопросы».

В этой статье впервые используется обозначение интеграла, хотя из-за сложностей при печати знак ?, примененный Лейбницем в рукописи, был заменен на f, что было исправлено в последующих изданиях. В статье, как и в первой от 1684 года, используется буква d для обозначения дифференциала.

Во второй статье он указывает, что дифференцирование и интегрирование являются взаимно обратными операциями, и формулирует основную теорему анализа: «Подобно степеням и корням в обычном исчислении, а также сумме и разности, J и d являются обратными». Он применяет это утверждение для доказательства теоремы, которую приписывает Барроу, для чего, как и при решении задачи де Бона, которой оканчивается первая статья, он решает дифференциальное уравнение. «Из изложенного в методе касательных очевидно, что

Следовательно, обратной является

¹/₂?x² = ?xdx».

Происхождение названия объясняется использованием латинского слова differentia — «разность». Отсюда понятие дифференциала и название «дифференциальное исчисление». Последовав совету Иоганна Бернулли, Лейбниц заменил изначальное название «суммарное исчисление» на «интегральное исчисление». Иоганн Бернулли также предлагал заменить символ ? буквой I — первой буквой слова «интеграл». В итоге они договорились сохранить название «интегральное исчисление», предложенное Бернулли, и символ ?, предложенный Лейбницем. В письме, датированном 28 февраля 1695 года, Лейбниц пишет Иоганну Бернулли: «В будущем было бы лучше с целью единообразия и гармонии не только между нами, но и во всей области изучения использовать термины сумм вместо твоих интегралов. Тогда, например, ?ydx будет означать сумму всех y, умноженных на соответствующий dx, или сумму всех этих прямоугольников. Я прошу этого главным образом потому, что в этой форме геометрические суммы, или квадратуры, лучше соответствуют арифметическим суммам и суммам рядов. Признаюсь, что открыл весь метод, рассматривая обоюдность сложения и вычитания, а затем в своих рассуждениях перейдя от последовательностей чисел к последовательностям отрезков и ординат».

Лейбниц опубликовал и другие статьи на тему анализа бесконечно малых. Профессор Норберто Куэста Дутари насчитал 27 статей, напечатанных в период с 1684 по 1708 год только в выпусках журнала Acta eruditorum. Первооткрыватели анализа различались и в этом: Лейбниц предпочитал публиковать статьи в научных журналах, чтобы быстрее познакомить общественность с полученными результатами, а Ньютон издавал их в виде книг и постоянно откладывал публикацию.