Эйлер и анализ бесконечно малых

Эйлер и анализ бесконечно малых

Если Ньютон и Лейбниц считаются создателями дифференциального и интегрального исчисления, то Эйлера можно назвать создателем математического анализа — области математики, куда входят оба эти раздела. В этом смысле его книги «Введение в анализ бесконечно малых» (1748), «Наставление по дифференциальному исчислению» (1755) и «Интегральное исчисление» (1768—1770) сыграли ключевую роль в оформлении структуры этой новой дисциплины.

Трактат «Введение в анализ бесконечно малых» стал для математического анализа тем же, что «Начала» Евклида для геометрии. В этом трактате Эйлер указывает, что функция является основным предметом изучения в анализе, систематизирует работы предшественников об элементарных функциях, изучает их, не прибегая к дифференциальному или интегральному исчислению, однако обильно использует бесконечно большие и бесконечно малые величины (см. приложение). Он также всеми возможными способами старается избежать геометрических рассуждений и чертежей, отдавая предпочтение аналитике и формулам. Структуру дифференциального исчисления он изложил во второй книге трилогии.

Хотя Эйлер был последователем Лейбница, в «Наставлении по дифференциальному исчислению» он понимает дифференциал как разницу, однако вносит изменения в исчисление Лейбница. С учетом поправок Эйлера понятие дифференциала приближается к понятию ньютоновской «исчезающей величины».

Извечные сомнения, касающиеся бесконечно малых, Эйлер развеял так. По его мнению, важнее было не то, что такое бесконечно малые величины, а то, как они себя ведут. В этом смысле для Эйлера бесконечно малые были равны нулю или в итоге приравнивались к нулю; важнее то, что эти величины могут делиться друг на друга. Результат подобного деления, по сути эквивалентного ⁰/₀, может равняться четко определенному конечному числу. Так, дифференциалы dx, dy играют главную роль при определении значения дроби dy/dx.. Исчисление описывает, как вычислить эту дробь, когда приращения «исчезают». В «Наставлении по дифференциальному исчислению» Эйлер описывает «метод определения пропорции исчезающих приращений, которые получают функции, когда аргументы функции получают одно из таких приращений». Иными словами, в анализе Эйлера вводится отношение приращений

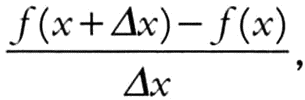
определяющее производную функции — понятие, которое заменило дифференциалы dx, dy, занимающие почетное место в исчислении Лейбница. Внесенные Эйлером изменения приблизили понятия дифференциального исчисления Лейбница к понятию предела, которое впоследствии использовал Коши.

В последнем труде трилогии Эйлера, «Интегральное исчисление», интегрирование описывается как операция, обратная дифференцированию. Интегрирование по-прежнему соответствовало понятию площади, но потеряло независимый характер, который отстаивал Лейбниц, что помогло Коши при введении понятия определенного интеграла.

ЭЙЛЕР ВЕЛИКИЙ

Эйлер был одним из величайших математиков всех времен и, вне всяких сомнений, лучшим математиком XVIII века. Он родился в 1707 году в Базеле, окончил местный университет, брал частные уроки у Иоганна Бернулли, одного из учеников Лейбница.

В 1727 году он переехал в Санкт-Петербург, был членом Петербургской академии наук с 1731 по 1741 год, затем переехал в Пруссию и был избран членом Берлинской академии наук. Несмотря на непростые отношения с прусским королем Фридрихом II, он прожил в Берлине 25 лет, после чего вернулся в Санкт-Петербург, где умер в 1783 году.

^{Портрет Леонарда Эйлера кисти Иоганна Георга Брюкнера.}