От Архимеда до XVII века
От Архимеда до XVII века
Лишь в XVII веке математики овладели приемами, описанными в трудах Архимеда, что ускорило появление анализа бесконечно малых. Следует упомянуть, что до того ученые Средневековья и эпохи Возрождения совершили несколько открытий, без которых было бы невозможно появление математического анализа. Однако важнейшие из них не связаны напрямую с исчислением, поэтому мы расскажем о них лишь вкратце. Речь идет в первую очередь о потере и повторном обретении и освоении наследия древних греков. Ключевую роль также сыграло распространение по всей Европе индийской системы счисления. Этот длительный и непростой процесс начался в X веке, а позднее, в XIII—XVI веках, на севере Италии возникли школы абака — образовательные центры для тех, кто занимался торговлей.
В конце XVI века десятичная система счисления также начала применяться для записи рациональных и иррациональных чисел. Решающую роль в ее распространении наряду с Франсуа Виетом (1540—1603) сыграл Симон Стевин (1548—1620), хотя использованная им нотация была не совсем удобной. Стевин, уроженец бельгийского города Брюгге, развил свою идею по причинам практического характера: «Десятичная система счисления есть класс арифметики, в основе которого лежит идея о прогрессии с основанием 10, где используются арабские цифры так, что в этой системе может быть записано любое число; и любая операция, с которой мы имеем дело в торговле, может быть выполнена с помощью только целых чисел, без использования дробей». Он предложил унифицировать единицы мер и весов, а также денежные единицы с применением новой системы счисления, но эта идея была воплощена в жизнь лишь после Великой французской революции.
Некоторое время спустя идее Стевина последовали другие авторы, которые использовали современную нотацию с точкой (или запятой) для отделения десятичной части от целой. Среди них был шотландский барон Джон Непер (1550—1617), один из создателей логарифмов. Логарифмы появились в начале XVII века и были тесно связаны с открытием анализа бесконечно малых. Независимо от Непера логарифмы придумал и швейцарец Иост Бюрги (1552—1632). Изначально они использовались как вспомогательные функции в числовых расчетах, чтобы упростить умножение больших чисел в астрономических вычислениях. Нетрудно представить, сколько времени нужно было потратить на умножение множества подобных чисел и сколь велик был риск ошибиться. Джон Непер писал: «Ничто не причиняет столько проблем при занятиях математикой и не делает вычисления столь неприятными и затруднительными, как умножение, деление и извлечение квадратных и кубических корней из больших чисел. Операции эти помимо потери времени в большинстве случаев являются источником ошибок».
Чтобы упростить умножение больших чисел, в то время использовался метод под названием простаферезис. В его основе лежала тригонометрическая формула, с помощью которой произведение преобразовывалось в сумму. По сути, Джон Непер создал логарифмы с целью упростить этот метод: ему были нужны таблицы, с помощью которых можно было бы напрямую преобразовывать произведения в суммы.
Метод простаферезиса заключается в следующем. Допустим, мы хотим перемножить два больших числа n и m. Пусть они состоят из восьми цифр каждое — стандартная ситуация для астрономических расчетов тех времен. Для этого найдем в таблице значений косинусов два числа а и b такие, что n = cos a, m = cos b. Затем с помощью таблицы определим значения cos (a — b) и cos (a + b), после чего применим следующую формулу:
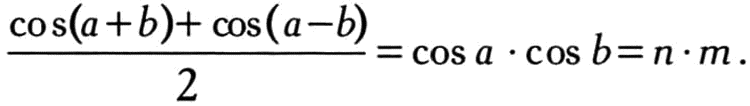
Если бы мы выполняли умножение напрямую, нам нужно было бы последовательно восемь раз умножить первое число на каждую цифру второго, после чего сложить восемь полученных чисел из восьми или девяти цифр каждое. С помощью вышеприведенной формулы и тригонометрических таблиц мы свели умножение к трем операциям сложения и простому делению на 2.
Метод простаферезиса был в некотором роде техническим инструментом: он позволял сэкономить время при расчетах, и его можно считать примитивным алгоритмом для вычислительной машины. Поэтому в течение определенного времени он держался в секрете и был доступен лишь немногим избранным. Непер, например, узнал об этом методе не самым обычным способом. Эта история больше напоминает сюжет приключенческого романа. Джон Крэйг, врач шотландского короля и друг Непера, в конце XVI века совершил путешествие в Данию, чтобы подобрать королю невесту. Корабль попал в шторм, и ему пришлось причалить к побережью вблизи лучшей обсерватории того времени, которую Тихо Браге построил на острове Вен между Данией и Швецией. Путешественников приютили в обсерватории, и, пока бушевал шторм, Крэйг познакомился с методом простаферезиса, а по возвращении в Шотландию обучил ему Джона Непера.
До XVII века было совершено крайне мало открытий, напрямую связанных с анализом бесконечно малых. Можно упомянуть о французском философе Николае Орезмском (ок. 1323—1382). Он дал примитивное определение понятия функции и ее графического представления: «Всё, что изменяется — реально ли измерить его или нет — можно вообразить как непрерывную величину, представленную отрезком». Он также внес вклад в изучение бесконечных рядов, впервые доказав, что сумма
1 + 1/2 + 1/3 + 1/4 + 1/5 + …
равна бесконечности.
ДОКАЗАТЕЛЬСТВО НИКОЛАЯ ОРЕЗМСКОГО
По словам самого Николая Орезмского, причина, по которой сумма гармонического ряда
1 + 1/2 + 1/3 + 1/4 + 1/5 + …
равна бесконечности, такова: «К величине, равной 1, прибавим 1/2, 1/3, 1/4 и следующие дроби, сумма которых равна бесконечности. В самом деле из членов этого ряда можно составить бесконечное число групп, сумма которых будет больше 1/2.
Так, 1/3 + 1/4 больше 1/2, так как каждое из двух слагаемых больше 1/4.
Аналогично,
1/5 + 1/6 + 1/7 + 1/8
больше 1/2, так как каждое из четырех слагаемых больше 1/8.
Аналогично
1/9 + 1/10 + … + 1/16
больше 1/2, так как каждое из восьми слагаемых больше 1/16, и так до бесконечности».