Максимум против минимума

Дифференциация нужна для того, чтобы выяснять, где функция достигает своего максимума, а где – минимума. При каком, например, значении x парабола y = x? – 8x + 10 достигает своей низшей точки?

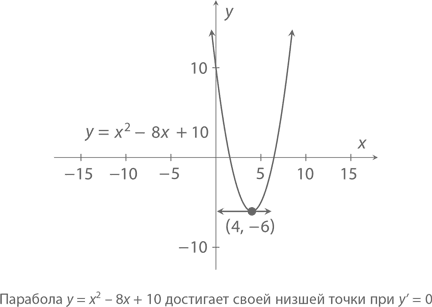
Как вы, наверняка, помните, проведенная через нее касательная должна иметь наклон 0. Так как y' = 2x – 8, уравнение 2x – 8 = 0 приведет нас к минимуму при x = 4 (кстати, y = 16 – 32 + 10 = –6). Для y = f(x) значение x, удовлетворяющее f'(x) = 0, называется критической точкой функции f. Функция y = x? – 8x + 10, например, имеет только одну критическую точку – x = 4.

Где же максимум? В нашем примере его попросту нет: значение y-координаты для x? – 8x + 10 может быть сколь угодно большим. Ограничить его можно одним единственным способом – определив для x пределы значений. Возьмем для примера 0 ? x ? 6. Тогда при x = 0 y будет равен 10, а при x = 6 – ?2, то есть критической точкой для этой функции является x = 0. Обобщение этого приводит нас к одной очень важной теореме.

Теорема (теорема об экстремуме функции в точке): Если дифференцируемая на отрезке функция y = f(x) принимает максимальное или минимальное значение в точке x*, то x* должна быть либо критической точкой f, либо граничной точкой отрезка.

Давайте на секунду вернемся в начало главы, к задаче с лотком. Нам нужно, по сути, максимизировать функцию

y = (12 – 2x)?x = 4x? – 48x? + 144x

где x должен находиться в диапазоне от 0 до 6. Нам нужно найти такой x, при котором значение y будет наибольшим. Так как наша функция представляет собой многочлен, ее производную можно найти как

y' = 12x? – 96x + 144 = 12(x? – 8x + 12) = 12(x – 2)(x – 6)

Следовательно, ее критическими точками будут x = 2 и x = 6.

А так как мы знаем, что при объеме, равном 0, и конечных точках, равных 0 и 6, объем будет минимальным, нам остается только одна критическая точка – x = 2. Именно она и даст нам максимум – y = 128 см?.