Важность бесконечной суммы: геометрические ряды

Начнем, пожалуй, с утверждения, принимаемого всеми математиками и кажущегося неправильным большинству непосвященных:

0,99999… = 1

То, что две эти величины очень близки друг к другу, не вызывает сомнений практически ни у кого. Но считать их одним и тем же числом?.. Несколько чересчур, правда? Неправда. Позвольте мне попробовать убедить вас в обратном. Поверьте, доказательств у меня так много, что хотя бы одно из них обязательно покажется вам правдоподобным.

Самое, пожалуй, простое исходит из утверждения, что

Умножаем обе стороны на 3 и получаем

Другое доказательство основано на методе, который мы использовали в главе 6 для периодических десятичных дробей. Обозначим бесконечную последовательность знаков после запятой переменной w, вот так:

w = 0,99999…

Умножим обе части на 10:

10w = 9,99999…

Вычтем первое уравнение из второго

9w = 9,00000…

и получим w = 1.

А вот доказательство, для которого алгебра вообще не нужна. Надеюсь, вы согласны с тем, что два числа могут считаться разными, если между ними расположено третье число, не равное ни первому, ни второму (например, их среднее арифметическое)? Пойдем от обратного: предположим, что 0,99999… и 1 суть разные величины. Какое же тогда число будет между ними? А если такого числа нет, значит, мы не можем утверждать, что они разные.

Два числа или две бесконечные суммы считаются равными в том случае, если они сколь угодно близки друг к другу, то есть разница между ними меньше любой положительной величины, будь то 0,1 или 0,0000001, или 1, деленное на триллион. Разница между 1 и 0,99999… – наглядный тому пример, и именно это дает математикам право утверждать, что 1 и 0,99999… суть одно и то же число.

Следуя той же логике, мы можем оценить бесконечную сумму следующего ряда:

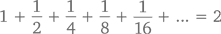
А еще мы можем найти ей физическое соответствие. Представьте, что вы стоите в двух метрах от кирпичной стены. Вы делаете шаг вперед – ровно на метр. Следующий шаг будет вполовину короче – полметра. Потом четверть метра, одна восьмая метра и так далее. С каждым шагом расстояние между вами и стеной сокращается ровно вполовину. Если проигнорировать физические ограничения на длину каждого следующего шага (в том числе и длину ваших ступней), то рано или поздно вы подберетесь вплотную к стене. Всего же вы пройдете ровно 2 метра.

То же можно представить и геометрически. Начнем с прямоугольника с длинами сторон 1 и 2 и площадью 2. Разделим его пополам, потом еще раз и еще – и так до бесконечности. Площадь первого сектора будет равна 1, второго – 1/2, третьего – 1/4 и так далее. Даже когда мы будем делить на n, стремящееся к бесконечности, мы не выйдем за пределы начального прямоугольника, а площади всех его секторов в сумме будут по-прежнему равны 2.

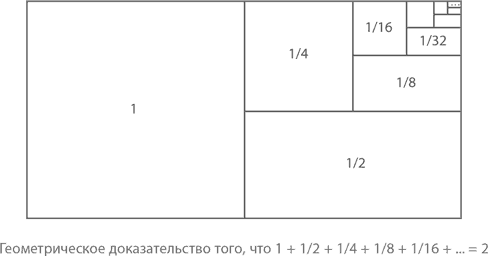
Алгебра позволяет нам подойти к решению задачи с точки зрения частичных, промежуточных сумм:

Эта закономерность подсказывает нам, что при n ? 0

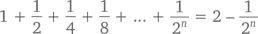
Доказать это можно либо с помощью метода индукции (см. главу 6), либо как частный случай формулы конечного геометрического ряда.

Теорема (конечный геометрический ряд): При x ? 1 и n ? 0

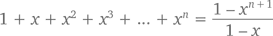
Доказательство 1 (метод индукции): При n = 0 формула говорит нам, что  что, конечно же, верно. Предположим теперь, что n = k, то есть наша формула превращается в

Она отлично работает и при n = k + 1, поэтому, добавив к обеим сторонам x^k+1, мы получим

что и требовалось доказать.?

А что, если мы немного схитрим, прибегнем к алгебре «со сдвигом»?

Доказательство 2: Предположим, что

S = 1 + x + x² + x³ +… + xⁿ

Умножим обе стороны на x:

xS = x + x² + x³ +… + xⁿ + x^{n + 1}

Вычтем xS и, проведя ряд упрощений, получим

S ? xS = 1 ? x^{n + 1}

Другими словами, S(1 ? x) = 1 ? x^{n + 1}, то есть

что и требовалось доказать.

Обратите внимание, что при x = 1/2 конечный геометрический ряд подтверждает выведенную нами ранее закономерность:

Чем больше n, тем ближе (1/2)n будет к 0. Следовательно, при n ? ?, у нас получится

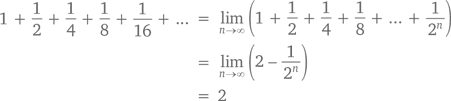
Отступление

На этот счет, кстати, есть одна шутка, понять которую сможет только математик. Бесконечное количество математиков заходит в бар. Первый заказывает полный бокал пива, второй – половину бокала, третий – четверть, четвертый – одну восьмую… Наконец, бармен не выдерживает и, воскликнув «Нет, ну есть же этому какой-то предел!», наливает им на всех две полные кружки.

Обобщая, можно сказать, что любое число в интервале от –1 до 1, возводимое во все бо?льшую и бо?льшую степень, все ближе и ближе подходит к нулю. В результате мы имеем крайне важный и полезный (бесконечный) геометрический ряд.

Теорема (геометрический ряд): При –1 < x < 1

Чтобы решить нашу последнюю задачу, примем x = 1/2:

Выглядит знакомо, не правда ли? Это потому что мы уже встречались с подобным рядом – в самом конце главы 11, когда с помощью исчисления старались показать, что функция y = 1/(1 – x) соответствует ряду Тейлора 1 + x + x² + x³ + x⁴ +….

А что еще мы можем «выжать» из этого ряда? Как насчет следующей суммы?

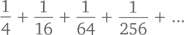
Если вынести за скобки дробь 1/4, убрав ее из каждого члена, получится

то есть при x = 1/4 мы можем упростить ряд до

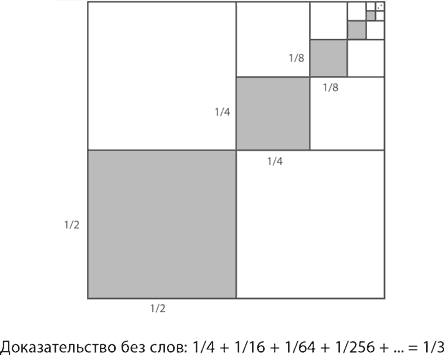
Доказать это можно практически без слов – просто посмотрите на рисунок ниже и обратите внимание, что закрашенные квадраты занимают ровно треть общей площади большого квадрата.

Геометрический ряд можно использовать также для доказательства нашей задачи с 0,99999…, ведь бесконечное количество знаков после запятой есть не что иное, как замаскированный бесконечный ряд. Просто примем x = 1/10 и получим

Формула геометрического ряда верна и тогда, когда х – комплексное число, при условии, что длина x – меньше 1. Например, мнимое число i/2 имеет длину 1/2, из чего следует, что

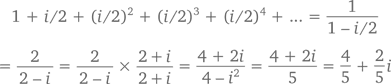
что показано на следующем графике, расположенном на комплексной плоскости.

И хотя формула конечного геометрического ряда верна для любого значения x ? 1, (бесконечный) геометрический ряд требует, чтобы |x| был меньше 1. Например, при x = 2 конечный геометрический ряд покажет нам (как мы уже выяснили в шестой главе), что

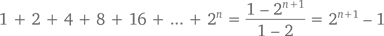
а бесконечный – что

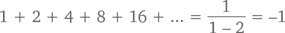
что выглядит нелепо (хотя это впечатление может быть и обманчивым: в предпоследнем разделе этой главы мы увидим вполне правдоподобное объяснение такого результата).

Отступление

Число положительных целых величин бесконечно:

1, 2, 3, 4, 5…

Равно как бесконечно и количество положительных четных целых величин:

2, 4, 6, 8, 10…

Считается, что первое множество (или число элементов, или степень бесконечности) приблизительно равно первому. В пользу этого утверждения говорит тот факт, что положительные целые и положительные четные целые можно объединить в пары, вот так:

Множество, способное к объединению в пары, называется счетным. Степень бесконечности у него, как правило, невелика. Любое множество, величины которого можно перечислить, является счетным, так как первый его элемент есть пара к 1, второй – к 2 и т. д. Множество всех целых величин

… –3, –2, –1, 0, 1, 2, 3…

перечислить от меньшего значения к большему не получится просто потому, что нет никакого «стартового» наименьшего значения. Зато получится перечислить их вот так:

0, 1, –1, 2, –2, 3, –3…

Следовательно, множество всех целых является счетным, а число его элементов равно числу элементов в множестве положительных целых.

А что насчет множества положительных рациональных величин? Напомню: рациональными называются числа, имеющие форму m/n, где и m, и n суть положительные целые. Хотите – верьте, хотите – нет, но и это множество будет счетным. Перечислить его элементы можно следующим образом:

то есть мы берем дроби в соответствии с суммой их числителей и знаменателей. Так как любая рациональная величина неизбежно появляется в списке, их множество будет счетным.

Отступление

А существуют ли вообще такие бесконечные множества, которые не являются счетными? Немецкий математик Георг Кантор (1845–1918) доказал, что все действительные величины, даже только те из них, что ограничены диапазоном от 0 до 1, образуют несчетное множество. Можно, конечно, попробовать перечислить их следующим образом:

0,1, 0,2…., 0,9, 0,01, 0,02…., 0,99, 0,001, 0,002…., 0,999…

и т. д. Но так мы никогда не выйдем за пределы величин с конечным количеством знаков. Число 1/3 = 0,333…, например, в нашем списке так и не встретится. Но, может, есть какой-нибудь другой, более эффективный способ перечисления? Кантор доказал, что его нет. Он пошел от обратного – предположил, что множество действительных величин является счетным. Он взял конкретный пример и начал с

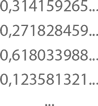
Доказать, что этот список не будет полным, можно, «придумав» такое действительное число, которое никогда в нем не появится. Можно взять, скажем, величину 0,r₁r₂r₃r₄…, где r₁ есть целое в интервале от 0 до 9, которое отличается от первого числа только первой цифрой (в нашем примере r₁ ? 3). Так же обстоит и с r₂: оно отличается от второго числа второй цифрой (у нас r₂ ? 7). И так далее. Таким образом у нас может получиться, скажем, 0,2674… – число, которое никогда не появится в списке, даже на миллионной позиции, потому что будет отличаться от нее миллионной цифрой. А значит, какой бы список вы ни создавали, всегда будут такие величины, которые в нем не появятся, следовательно, множество действительных чисел является несчетным.

Эта схема известна под названием «канторовский диагональный процесс», но мне больше по душе «доказательство через кантор-аргумент» (кхм, прошу прощения).

По сути, мы только что показали, что, несмотря на бесконечность рациональных величин, величин иррациональных все же больше. Просто выберите случайное действительное значение, лежащее на оси, и оно почти наверняка окажется иррациональным.

Бесконечные ряды очень часто появляются при решении задач, связанных с вероятностью. Предположим, что вы кидаете два шестигранных кубика, причем кидаете до тех пор, пока в сумме у вас не выпадет 6 или 7. Если 6 выпадает раньше 7, вы выиграли, если наоборот – проиграли. Каковы ваши шансы на победу? Количество возможных комбинаций равно 6 ? 6 = 36. Пять из них дают в сумме 6 (а именно (1, 5), (2, 4), (3, 3), (4, 2), (5, 1)), шесть – 7 ((1, 6), (2, 5), (3, 4), (4, 3), (5, 2), (6, 1)). Следовательно, ваши шансы на победу составляют меньше 50 %. Но сколько именно? Всего значимых для вас комбинаций 5 + 6 = 11, в остальных случаях кубики придется бросать вновь. Из этих одиннадцати пять приведут вас к выигрышу, шесть – к поражению. Значит, ваши шансы равны 5/11.

К тому же ответу можно прийти и с помощью геометрического ряда. Шансы на выигрыш при первом броске равны 5/36. А при втором? Чтобы он вообще состоялся, при первом броске вам надо выбрость что-то, кроме 6 или 7. Не забываем, что оптимальный для нас результат – 6. Общая вероятность выбросить 6 или 7 при первом броске – 5/36 + 6/36 = 11/36, выбросить другую комбинацию – 25/36. Чтобы определить вероятность выигрыша при втором броске, умножим это число на вероятность выбросить 6 при любом броске – 5/36, – в результате получим (25/36)(5/36). Для третьего броска получим уже (25/36)(25/36)(5/36), для четвертого – (25/36)?(5/36) и т. д. Сложив все вместе, получим

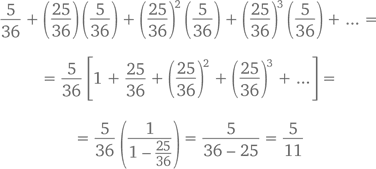
что и требовалось доказать.?