Правила алгебры

Начнем с загадки. Найдите число, которое становится в три раза больше, если к нему прибавить 5.

Чтобы ее решить, заменим неизвестное нам число буквой х. Добавление пятерки дает нам х + 5, утроение – 3х. Мы хотим, чтобы эти две записи были равными, поэтому нам придется решать уравнение

3x = x + 5

Уберем по одному х из обеих его частей и получим

2x = 5

(смотрите, откуда берется 2x: 3x – x – то же, что и 3x – 1x, то есть 2x). Разделим обе части уравнения на 2:

x = 5/2 = 2,5

Можем проверить правильность ответа: 2,5 + 5 = 7,5, Тот же ответ получаем, умножая 2,5 на 3.

Отступление

А вот еще один фокус, в сути которого можно легко разобраться с помощью алгебры. Запишите любое трехзначное число, цифры в котором идут по убывающей (например, 842 или 951). Затем запишите эти числа в обратном порядке и вычтите второе число из первого. Какой бы ответ у вас ни получился, запишите в обратном порядке и его, а затем сложите эти два числа. Вот пример с числом 853:

Попробуйте другое число. Что вышло? А то, что, если четко и правильно выполнять все инструкции, вы всегда будете получать 1089! Как так?

Алгебра, помоги! Итак, начинаем мы с трехзначного числа abc, в котором a > b > c. Точно так же, как и 853 = (8 ? 100) + (5 ? 10) + 3, число abc равняется 100a + 10b + c. Записав его справа налево, получим число cba, равное 100c + 10b + a. Вычитание дает нам

(100a + 10b + c) – (100c + 10b + a) = (100a – a) + (10b – 10b) + (c – 100c) = 99a – 99c = 99(a – c)

Другими словами, нам надо умножить полученную разность на 99. А раз в изначальном нашем числе цифры идут по убыванию, a – c даст нам как минимум 2: 2, 3, 4, 5, 6, 7, 8 или 9. Следовательно, выполнив вычитание, мы гарантированно получим

198, 297, 396, 495, 594, 693, 792 или 891.

И каждое из этих чисел, если мы прибавим его к его «зеркальному» двойнику, даст

198 + 891 = 297 + 792 = 396 + 693 = 495 + 594 = 1089

– пару, неизбежно дающую в сумме 1089.

Этот пример отлично иллюстрирует то, что я называю золотым правилом алгебры: совершайте с одной частью уравнения те же действия, что и с другой его частью.

Например, нам нужно найти x в уравнении

3(2x + 10) = 90.

Наша основная задача – изолировать х, и первый шаг на пути к этому – разделить обе части на 3, чтобы упростить решение:

2x + 10 = 30.

Второй шаг – избавиться от 10, которую надо вычесть и слева и справа, то есть

2x = 20.

Наконец делим все на 2, упрощая тем самым левую часть, в итоге получая

x = 10.

Ну и проверим ответ, конечно – это никогда не помешает: При x = 10 3(2x + 10) = 3(30) = 90, что верно. Интересно, есть ли у этого уравнения другое решение? Ответ – нет, потому что любое значение х должно удовлетворять не только этому, но и любому последующему уравнению, так что x = 10 – единственный верный ответ.

А вот алгебраическая задачка из реальной жизни: в 2014 г. газета New Tork Times рассказала читателям, что фильм «Интервью» (The Interview) компании «Сони Пикчерз» в первые четыре дня после релиза собрал в Интернете $15 млн. Но компания не уточнила, сколько из этой суммы принесли покупки фильма в Сети ($15), а сколько – платные просмотры ($6); зато мы знаем, что всего было совершено около 2 млн транзакций. Чтобы эту задачку решить, обозначим количество онлайн-продаж буквой S, количество платных просмотров – буквой R. Составим уравнение

S + R = 2 000 000.

А так как каждая транзакция по продаже – это $15 прибыли, а по просмотру – $6, уравнение преобразуется:

15S + 6R = 15 000 000

Возможность привести первое уравнение к виду R = 2 000 000 – S позволяет нам преобразовать и второе уравнение:

15S + 6(2 000 000 – S) = 15 000 000.

или 15S + 12 000 000 – 6S = 15 000 000, в котором у нас из неизвестных остается только S. Продолжаем упрощать:

9S + 12 000 000 = 15 000 000.

Вычтем из обеих частей 12 000 000:

9S = 3 000 000.

Значит, S примерно равняется трети миллиона: S ? 333 333, а R = 2 000 000 – S ? 1 666 667 (проверим: общий доход составил $15 ? 333 333 + $6 ? 1 666 667 ? $15 000 000).

Теперь самое время обсудить правило, которым мы в этой книге уже использовали и продолжим использовать, хотя до этого напрямую о нем не говорили. Называется оно «закон дистрибутивности» и работает тогда, когда у вас в одной задаче или одном уравнении есть одновременно сложение и умножение. Согласно этому закону, для любых чисел a, b и с верно следующее:

a(b + c) = ab + ac.

Это правило следует использовать при умножении однозначного числа на двузначное, например,

7 ? 28 = 7 ? (20 + 8) = (7 ? 20) + (7 ? 8) = 140 + 56 = 196.

Очень полезная штука, когда дело доходит до счета. Допустим, у нас есть 7 кошельков с монетами: по 20 золотых и 8 серебряных монет в каждом. Сколько у нас всего монет? С одной стороны, можно подойти к проблеме так: в каждом кошельке по 28 монет, значит, всего их 7 ? 28. С другой стороны, можно посчитать отдельно монеты разного достоинства: 7 ? 20 золотых и 7 ? 8 серебряных, значит, всего: (7 ? 20) + (7 ? 8). Следовательно, 7 ? 28 = (7 ? 20) + (7 ? 8).

Закон дистрибутивности можно выразить и геометрически, начертив прямоугольник и разбив его на два части, как на рисунке.

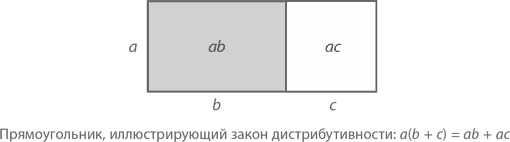
Как видим, площадь прямоугольника равна a(b + c). Однако левая часть выглядит как ab, правая – как ac, поэтому в итоге у нас получается ab + ac. Отличная иллюстрация к закону дистрибутивности при условии, что a, b и c – положительные величины.

Иногда, кстати, его можно применить одновременно и к числам, и переменным, например,

3(2x + 7) = 6x + 21

«Читать» это уравнение можно двумя способами: слева направо и справа налево. В первом случае мы видим 3, умноженное на 2x + 7. Во втором мы разлагаем 6x + 21 на сомножители, «вытягивая» тройку из 6x и 21.

Отступление

Почему «минус» на «минус» при умножении дают «плюс»? Иными словами, с чего бы вдруг (–5) ? (–7) = 35? У учителей всегда наготове с десяток самых разных объяснений, начиная с аннулирования долгов и заканчивая железобетонным «ну, потому что вот так». Но настоящая причина – в том, что закон дистрибутивности работает по отношению ко всем числам, не только положительным. А раз уж мы применяем его и к отрицательным числам (и к нолю, кстати), будьте готовы столкнуться с последствиями. Давайте посмотрим, почему.

Допустим, мы примем тот факт, что –5 ? 0 = 0, а –5 ? 7 = –35. (Для этих примеров тоже имеются свои доказательства, очень близкие к тому, что мы выстраиваем сейчас, но большинство с радостью просто принимают эти утверждения на веру.) Взгляните-ка вот на что:

– 5 ? (–7 + 7)

Чему это равно? С одной стороны, это все то же –5 ? 0, равное, как нам хорошо известно, нолю. С другой стороны, использовав закон дистрибутивности, мы получим ((–5) ? (–7)) + (–5 ? 7). Следовательно,

((–5)) ? ((–7)) + (–5 ? 7) = ((–5) ? (–7)) – 35 = 0

А если ((–5) ? (–7)) – 35 = 0, мы вынуждены признать, что (–5) ? (–7) = 35. Обобщая, можно сказать, что закон дистрибутивности утверждает, что для всех значений a и b будет верно следующее: (–a) ? (–b) = ab.