Закономерности треугольника Паскаля
Вот вам во всей его красе треугольник Паскаля:
Треугольники уже знакомы нам по главе 1, так что мы хорошо знаем, насколько интересные закономерности могут появляться из организованных таким образом чисел. Еще более интересные (и куда более красивые) закономерности получатся в треугольнике чисел 
о которых мы только что узнали. Такой треугольник называется Паскалевым – тот, который изображен чуть выше. У нас есть формула 
Давайте превратим все ее символы в числа и поищем закономерности (см. изображение треугольника чуть ниже). Большинство из них будут подробно описаны в этой главе, но, если объяснения вдруг покажутся вам скучными, можете смело их пропускать и просто наслаждайтесь стройной красотой самих закономерностей.
Верхний (или нулевой) ряд представлен одним-единственным значением – 
(не забывайте: 0! = 1). Каждый ряд начинается с единицы и ею же заканчиваются, потому что
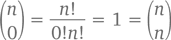
Взгляните на пятый ряд:
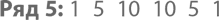
Обратите внимание, что второе число в нем – 5, да и в принципе вторым числом ряда n будет n. Это все из-за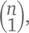 
за того, что количество способов выбрать один объект из множества n равно n. Также стоит обратить внимание, что каждый ряд
геометрически симметричен: чисел до центральной оси столько же, сколько и после нее. В том же самом 5 ряду мы видим
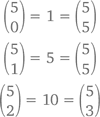
В целом же закономерность говорит о том, что
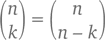
Отступление
У таких симметричных отношений есть два объяснения. Первое – алгебраическое – с помощью формулы
Но так ли уж сильно она нам тут нужна? Почему, например, 
Число 
обозначает количество вариантов выбора 3 сортов мороженого из десяти (в вазочке, не в рожке). Но ведь это то же самое, что считать варианты выбора тех 7 сортов, которые мы не купим.
Следующая закономерность, которую легко заметить, заключается в том, что во всех, кроме 1-го, рядах каждое число есть, по сути, сумма двух других – тех, которые находятся прямо над ним. Посмотрите, например, на 9 и 10 ряды треугольника. Потрясающе, правда? Называются эти отношения правилом Паскаля.
Почему так происходит? Когда мы смотрим на равенство 120 = 36 + 84, мы, по сути, видим
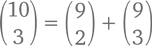
Чтобы в этом разобраться, давайте попробуем ответить на один вопрос. Если имеется 10 сортов мороженого, сколько вазочек можно собрать из 3 шариков разных сортов (порядок шариков при этом не важен)? С одной стороны, мы уже посчитали это количество как 
Но есть и другой способ. Допустим, один из предлагаемых нам сортов мороженого – ванильное. Сколько вазочек у нас получится без него? Ответ – 
потому что тогда мы будем выбирать свои 3 сорта из 9 оставшихся. А сколько вазочек получится с ним? Конечно же,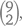 
ведь нам останется выбрать только 2 сорта из 9 оставшихся. Получается, что общее количество вазочек будет равно 
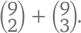Какой из этих ответов верен? И в том и в другом случае мы следовали абсолютно верной логике, поэтому и в том и в другом случае мы дали абсолютно верный ответ и получили абсолютно одинаковые результаты. Та же логика (или та же алгебра, если хотите) приводит нас к идее, что для каждого значения k от 0 до n
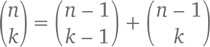
А теперь давайте посмотрим, что будет, если мы сложим все числа каждого ряда Паскалева треугольника (см. ниже).
Закономерность предполагает, что сумма всегда будет представлять собой степень двойки. Алгебраически: сумма чисел ряда n будет равна 2n. Как так получается? Эту закономерность можно описать и по-другому: сумма чисел (числа) 1-го ряда равняется 1 и затем удваивается от ряда к ряду. Объяснением этому служит правило Паскаля, природу которого мы только что объяснили, а обоснованность – доказали. Например, когда мы складываем между собой числа 5-го ряда и трансформируем их в зависимости от их связи с 4-м рядом, получается
1 + 5 + 10 + 10 + 5 + 1
то есть буквально удвоенная сумма чисел 4-го ряда. То же продолжается и дальше, вниз от вершины треугольника и до бесконечности.
С точки зрения биноминальных коэффициентов правило утверждает, что сумма чисел ряда n выглядит так:
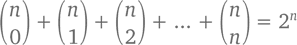
что несколько неожиданно, поскольку отдельные значения соответствуют факториалам и являются делимыми самых разных чисел. И все же общая сумма основана на 2 и простом множителе.
Еще один способ объяснить эту закономерность – подсчет, а именно – комбинаторное доказательство. Чтобы объяснить сумму чисел 5 ряда (который ничем принципиально не отличается от ряда n), давайте вернемся к прилавку с мороженым, где на этот раз осталось всего лишь 5 сортов. Сколькими способами мы можем заполнить нашу вазочку? Единственное ограничение – сорта не должны повторяться. Мы можем взять 0, 1, 2, 3, 4 или 5 разных сортов, а порядок шариков не важен. Сколько получится вазочек с 2 шариками? Как мы уже знаем, посчитать их можно как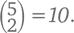 
Всего же, в зависимости
от количества шариков в вазочке и руководствуясь правилом суммы, получаем
вариантов, что можно упростить до 1 + 5 + 10 + 10 + 5 + 1. С другой стороны, мы можем ответить на тот же вопрос, использовав правило произведения. Вместо того чтобы торопиться подсчитывать, сколько всего шариков может оказаться в вазочке, мы можем взять каждый из предлагаемых сортов и решить, покупать его или нет. Например, у нас есть 2 варианта выбора для шоколадного мороженого (берем или нет), 2 – для ванильного (берем или нет) и т. д. для всех 5 сортов (имейте в виду, что, решив не брать ни один из сортов, мы останемся с пустой вазочкой, что условия нашей задачи вполне допускают). Значит, возможных комбинаций будет
2 ? 2 ? 2 ? 2 ? 2 = 25
А раз в обоих случаях мы шли верным путем,
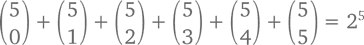
чего и следовало ожидать.
Отступление
Тот же комбинаторный принцип доказывает, что, если посчитать сумму каждого второго числа в ряду n, у нас получится 2n–1. В этом нет ничего удивительного, когда мы берем нечетные ряды, вроде пятого, где числа, которые мы складываем (1 + 10 + 5), совпадают с теми, которые мы пропускаем (5 + 10 + 1). Поэтому-то у нас и получается ровно половина от 2n. Но ведь это работает и в четных рядах. Например, в четвертом: 1 + 6 + 1 = 4 + 4 = 2?. Обобщая, мы можем утверждать, что в любом ряду n ? 1
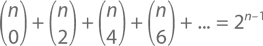
Почему? Левая сторона считает вазочки с четным количеством шариков мороженого (при ассортименте из n сортов и при условии, что в своем выборе мы не повторяемся). Но ту же вазочку можно получить, просто выбрав сорта от 1 до n – 1. У нас есть 2 варианта выбора для первого сорта (берем или нет), 2 – для второго и т. д., вплоть до сорта n – 1. Но вот для самого последнего сорта выбора у нас нет (вернее, только один) – мы же хотим, чтобы общее количество сортов было четным. Значит, и четное количество вазочек будет равно 2n–1.
Если представить треугольник Паскаля как прямоугольный, можно увидеть еще больше закономерностей. Первый (или 0) столбец состоит из одних единиц, второй (или 1) – из положительных целых 1, 2, 3, 4 и так далее. Третий (или 2) столбец, начинающийся с 1, 3, 6, 10, 15… тоже нам хорошо знаком, ведь это треугольные числа, с которыми мы уже сталкивались в главе 1. Они также могут быть представлены как
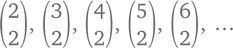
Значит, столбик k будет состоять из чисел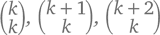 
и т. д.
А теперь смотрите, что произойдет, когда мы сложим между собой несколько первых чисел любого столбца. Возьмем, например, первые 5 чисел 3 столбца (см. ниже). Получаем 1 + 3 + 6 + 10 + 15 = 35 – число, которое видим справа по диагонали от 15. Другими словами,
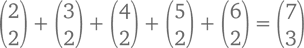
Называется эта закономерность правилом хоккейной клюшки, ведь форма обводки складываемых чисел, входящих в Паскалев треугольник, вместе с их суммой напоминает именно этот спортивный снаряд. Чтобы понять, на чем эта закономерность основана, представим себе хоккейную команду из семи игроков. У каждого на свитере порядковый номер: 1, 2, 3, 4, 5, 6, 7. Сколько можно составить троек для проведения тренировки?
Поскольку порядок не важен, у нас получится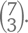 
А теперь давайте попробуем найти ответ на эту задачу, разбив ее на несколько поменьше. Во сколько троек будет входить игрок под номером 7? Иными словами, в каком количестве тренировок будет мелькать свитер с самым большим номером? Так как одно место в тройке занято семеркой, на остальные два места у нас остается 
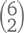вариантов. Идем дальше. Сколько тренировок посетит хоккеист с цифрой 6 на свитере? Включаем в свою задачу 6, исключаем из нее 7 и получаем 
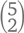вариантов для двух «вакансий». Точно так же нужно будет посчитать 
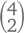вариантов для номера 5, 
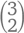– для номера 4 и 
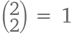– для номера 3. Так как самыми большими числами могут быть 3, 4, 5, 6 или 7, мы просчитали все возможные варианты, поэтому тройка может быть сформирована 
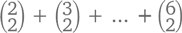способами – и это то же число, что было обозначено в левой части предыдущего уравнения. Обобщая, можно сказать, что
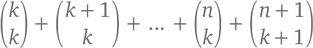
Давайте используем эту формулу для решения важной задачи, которая, без сомнения, заботит ваш ум каждый год во время новогодних каникул. Возьмем за основу популярную английскую народную песенку «Двенадцать дней Рождества»[13]: в первый день ваша настоящая любовь подарила вам 1 подарок (куропатку). На второй день – 3 подарка (куропатку и 2 горлиц). На третий – целых 6 (куропатку, 2 горлиц и 3 курочек). И так далее. Вопрос: сколько подарков у вас будет через 12 дней?
На n-ный день вы будете счастливым обладателем
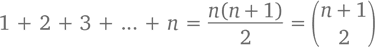
подарков (получилось это из нашей суперполезной формулы для треугольных чисел или из правила клюшки при k = 1). Так вот, первый день – 
подарок, второй день – 
подарка и т. д., вплоть до 12-го дня, в который вы получите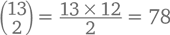 
подарков. А правило хоккейной клюшки приводит нас к общему их количеству:
То есть если открывать по подарку каждый день – вам хватит их почти до конца года (ну, один можно пропустить в день рождения)!
Давайте теперь cпоем песенку, чтобы отпраздновать свой успех. Называется она «N-ный день Рождества».
В n-ный день Рождества послала мне любовь моя верная
n удивительных лакомств
n – 1 с одним вкусом,
n – 2 с другим; и остальных вкусностей
…
5 (плюс 10) всяких вкусностей!
А через n дней,
Усевшись считать подарки,
Сколько же я насчитал(а)?
Ровно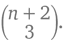 
А вот одна из самых странных закономерностей Паскалева треугольника. На рисунке ниже отмечены все нечетные числа. Присмотритесь к ним и увидите в большом треугольнике несколько маленьких.
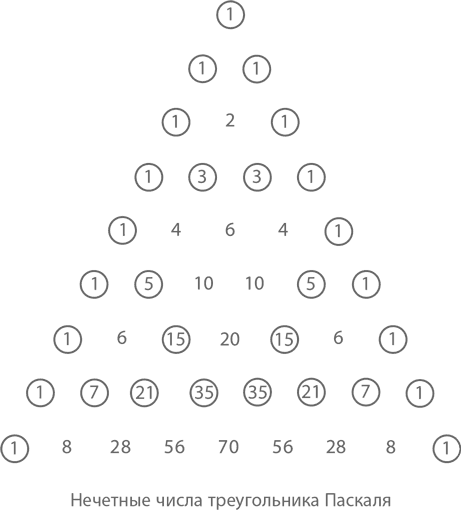
А теперь давайте сделаем вот что: сначала продлим большой треугольник до 16 рядов, а затем заменим все нечетные числа единицами, а все четные – нолями. Обратите внимание, что под каждой парой нолей, равно как и под каждой парой единиц, стоит ноль. Причина этого – в том, что при сложении 2 четных или 2 нечетных чисел сумма будет выражена четным числом.
Не будем на этом останавливаться: посмотрим на еще больший треугольник – из 256 рядов, – в котором все нечетные числа заменены черными квадратиками, а все четные – белыми.
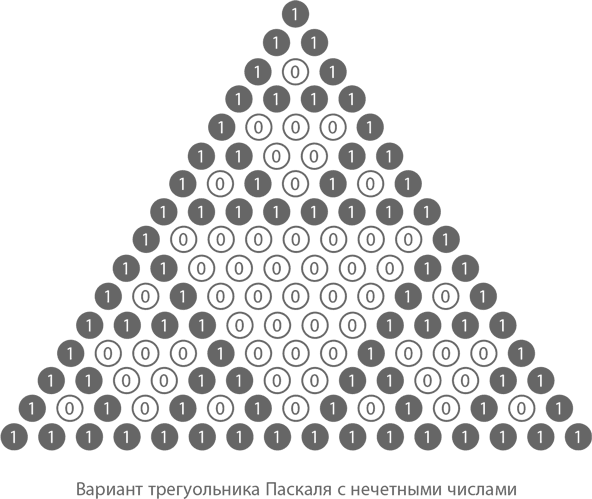
По сути своей данная фигура – это фрактал, или рекурсивное изображение, известное так же как треугольник Серпинского, – один из огромного количества сокровищ, скрытых в глубинах Паскалева клада. А вот еще один. Сколько всего нечетных чисел в каждом ряду треугольника Паскаля? Смотрим на ряды с 1 по 8 (без нулевого) и считаем: 2, 2, 4, 2, 4, 4, 8, 2 и т. д. Вроде бы никакой закономерности. Кроме того, что у нас всегда получается число, являющееся степенью 2. Это и есть та самая, нужная нам закономерность. Обратите внимание, что ряды, количество нечетных чисел в которых равно именно 2, – это 1, 2, 4 и 8-й. То есть обозначены они числами, которые сами являются степенью 2. Для более общего вывода нам нужно вспомнить, что любое целое число, которое больше 0 или равно ему, можно получить от сложения степеней числа 2. Смотрите сами:
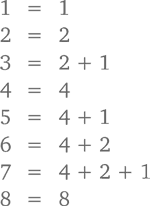
В рядах 1, 2, 4 и 8 (порядковые номера которых суть степени 2) у нас по 2 нечетных числа. В рядах 3, 5 и 6 (порядковые номера которых суть сумма двух степеней 2) у нас по 4 нечетных числа. В ряду же 7 (порядковый номер которого есть сумма трех степеней 2) – 8 нечетных чисел. Отсюда следует удивительное по своей красоте правило. Если n есть сумма p различных степеней числа 2, количество нечетных чисел в ряду n равняется 2p. Сколько, например, нечетных чисел будет в 83-м ряду? Так как 83 = 64 + 16 + 2 + 1 (то есть сумма четырех степеней 2), наш ответ будет 24 = 16!
Отступление
Не будем на этом подробно останавливаться, но, если вам интересно, 
будет нечетным числом всякий раз, когда
k = 64a + 16b + 2c + d
при a, b, c и d равных нолю или единице. Говоря точнее, k будет равно одному из этих чисел:
0, 1, 2, 3, 16, 17, 18, 19, 64, 65, 66, 69, 80, 81, 82, 83
И под самый конец главы – еще одна закономерность. Мы уже видели, что происходит, если сложить числа в рядах (степень 2) и столбцах («хоккейная клюшка») Паскалева треугольника. А что будет, если сложить их по диагонали?
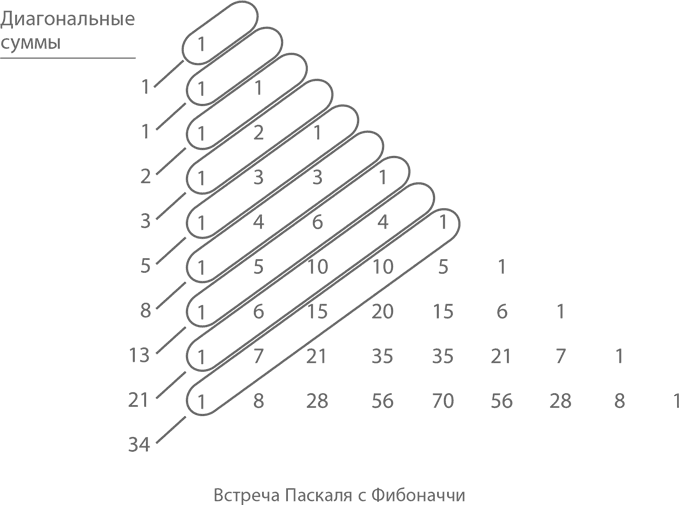
Смотрите, какие суммы выходят:
1, 1, 2, 3, 5, 8, 13, 21, 34
Не буду томить вас. Это числа знаменитой последовательности Фибоначчи, которая окажется в центре нашего внимания в следующей главе.