Объясняет Ньютон

Исполнение может быть трудным, но физика этой свечки относительно проста. Основной силой является гравитация, и путь мяча может быть рассчитан с помощью уравнений динамики Ньютона. Если предположить отсутствие сопротивления воздуха, мяч будет следовать траектории, схожей с показанной на рисунке 5.1. Как и все подобные траектории, форма ее параболическая. Я предполагаю, что скорость мяча постоянна. Скорость, направленная вниз, увеличивается с течением времени, поскольку сила тяжести заставляет мяч ускоряться относительно земли[50]. Гравитация обеспечивает постоянное ускорение, поэтому первоначальная скорость восходящего потока положительна, но уменьшается на равную величину в каждый момент времени.

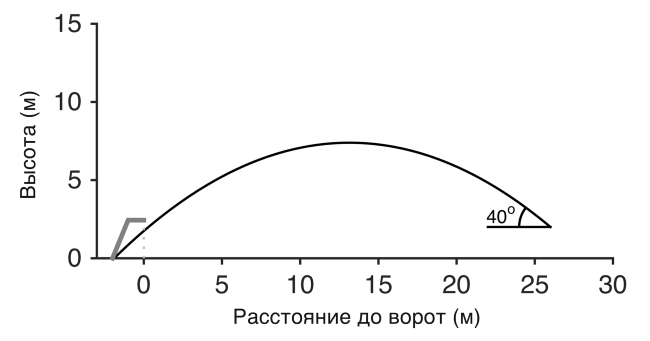
Рисунок 5.1. Траектория удара Златана Ибрагимовича согласно ньютоновской физике.

Она равна нулю, когда мяч находится на максимальной высоте, а затем становится отрицательной, когда мяч опускается. В результате траектория мяча симметрична относительно максимума – путь вверх и путь вниз идентичны.

Все это выглядит довольно просто. Всего лишь случай запуска мяча под правильным углом и с правильной скоростью, после чего гравитация берет все в свои руки и мяч оказывается в сетке ворот. Но проблема в том, что связь между углом запуска и тем, куда попадает мяч, не так проста. Рисунок 5.2 представляет собой график шести разных попыток, в которых запуск выполнялся под разным углом. Два раза мяч попал в ворота и четыре прошел мимо.

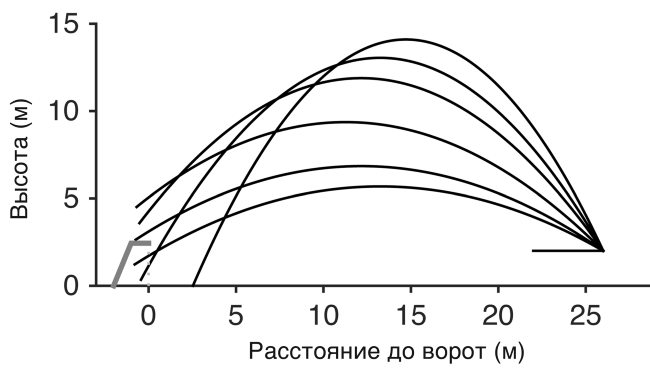
Рисунок 5.2. Как траектория свечки от Златана Ибрагимовича определяется углом запуска.

Все эти удары имели одну и ту же начальную скорость – 17 метров в секунду, но результаты отличаются. Не долетит мяч, попадет в ворота или полетит выше – итог зависит от сложной связи между скоростью и углом. Мы можем изучить эту связь, решая уравнения динамики. Отображение того, как мяч перемещается со временем, – это задача, которую вы можете попросить решить на уроке математики в средней школе. Чтобы узнать, попадает ли мяч в цель, нам нужно перегруппировать показатели, чтобы найти условие, при котором мяч будет проходить под перекладиной и при этом не касаться земли. Это несложно, но требует некоторых математических шагов[51].

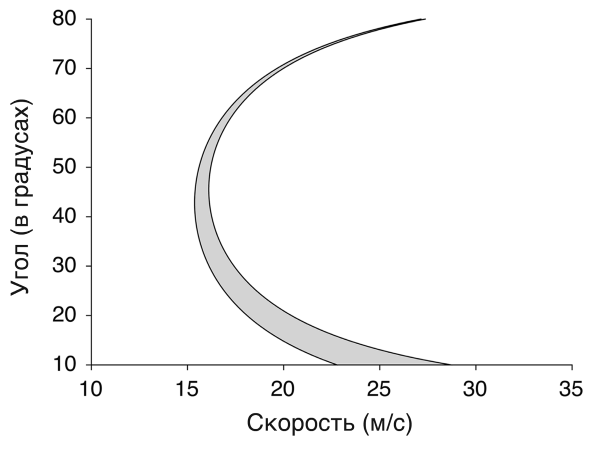
Рисунок 5.3. Как начальная скорость и угол запуска влияют на попадание мяча в цель. Серая область показывает комбинации углов и скоростей, при которых Златан забьет. Сочетания справа от серой области посылают мяч над перекладиной, а комбинации слева заставляют мяч скакать перед воротами.

На рисунке 5.3 показаны комбинации углов и скоростей, при которых мяч достигает ворот. Подумайте о том, как Златан может выбрать точку на этом чертеже. Например, он мог ударить мяч со скоростью 25 метров в секунду и под углом 40°, и в этом случае мяч пролетел бы над перекладиной. Или он мог ударить его со скоростью 15 метров в секунду и под углом 30°, но тогда тот бы упал и скакал перед воротами. Если Златан выберет вариант, показанный мной на рисунке 5.1 (ударит со скоростью 16 метров в секунду и под углом 40°), то мяч окажется в воротах. Комбинации, которые приведут к голу, занимают лишь небольшой кусочек в обилии всевозможных углов и скоростей. Если мяч послан слишком сильно, он перелетит над перекладиной; если от ноги, он летит под слишком большим или слишком маленьким углом, он не долетит и защитники справятся с ним. Сила также должна быть приложена правильно. Узкая полоска вариантов формируется таким образом, что без математики сложно предсказать, что произойдет. Мяч, полетевший под углом 19° со скоростью 20 метров в секунду, попадет в ворота. Однако если ударить чуть сильнее, то мяч пройдет выше перекладины. При угле запуска в 65° мяч поднимется очень высоко, затем опустится вниз и окажется в сетке. Это очень сложный удар, ведь даже небольшое увеличение угла или уменьшение скорости приведет к тому, что мяч будет скакать перед воротами.

Так как же Златан смог исполнить этот удар правильно? В этом голе была определенная удача. Харт оказался вне своей штрафной и не сумел головой выбить мяч далеко, поэтому Златан оказался в нужном месте в нужное время. Но когда он получил шанс, то идеально приложился к мячу. После многократных просмотров записи (с включенными комментариями) я предполагаю, что мяч покинул ногу Златана со скоростью 16 метров в секунду под углом 40°, как показано на рисунке 5.1. Выбрав не самую большую скорость, Златан оставил зазор для ошибки в выборе угла. Любой угол между 30° и 50° дает одинаковый итог: мяч оказывается в сетке. Если бы он ударил сильнее (например, со скоростью 20 метров в секунду), погрешность была бы намного меньше. Даже с учетом удара через себя Златан минимизировал вероятность совершения ошибки.