1, 2, 4, 8, 16…

Футбольный заряд лучше всего звучит тогда, когда его поют все болельщики на стадионе. Иногда, например, в случае с «You’ll Never Walk Alone» и «El Cant del Bar?a» перед самым началом матча на стадионе включают гимн и болельщики поют в такт музыки. Однако в подавляющем большинстве случаев пение на стадионах начинается спонтанно. Ответ «Копа» на излишне оптимистичный удар Джеррарда – яркий тому пример. Один фанат начинает, его друг рядом подхватывает: 1 + + 1 = 2. Если каждый из них вдохновляет на пение еще одного фаната, тогда мы получаем следующее равенство: 2 + 2 = 4, затем 8, затем 16. Сначала рост числа фанатов небольшой, но в каждый момент времени количество людей, которые начинают петь, удваивается. Когда мы произведем умножение на два в 13-й раз, мы увидим, что 4096 фанатов вдохновили на пение еще 4096 фанатов, а это значит, что среди поющих у нас уже будет 8192 человека. Именно так работает геометрическая прогрессия: мы продолжаем умножать число поющих фанатов само на себя и вскоре получаем огромный показатель.

Увеличение количества поющих болельщиков напоминает процесс размножения бактерий на куске сочного стейка. В благоприятных условиях клетки кишечной палочки могут делиться каждые 20 минут. Если достать мясо из холодильника и оставить его на столе на ночь, из одной бактерии может получиться несколько миллионов[111]. Лия Эдельштайн-Кешет, специалист в области математической биологии, в своей книге пришла к (не-)логическому выводу по поводу такого роста количества бактерий[112]. При увеличении числа бактерий в два раза каждые 20 минут уйдет менее двух дней на то, чтобы вес бактерии, равный 10–12 граммам, вырос до показателя планеты Земля. С учетом всего этого вряд ли кому-то покажется удивительным, что на то, чтобы чант подхватил весь стадион, уходит всего несколько секунд.

И хотя модель размножения бактерий, разработанная Лией, может кого-то повеселить, она явно неправильная. Чтобы такая модель работала, наша планета должна быть одним огромным куском мяса. Но это не так. Оптимальное описание роста должно учитывать некие ограничения. Если бы у нас было 20 тысяч болельщиков «Вест Хэм Юнайтед», распевающих «I’m Forever Blowing Bubbles» («Я всегда надуваю пузыри») на «Аптон Парк», вмещающем 35 016 человек, другим 20 тысячам поющих фанатов просто не хватило бы места. После переезда «Вест Хэма» на Олимпийский стадион матчи команды могут посетить примерно 60 тысяч болельщиков, однако уйдет ненамного больше времени на то, чтобы пение охватило весь этот стадион. Если мы умножим 40 тысяч на два, мы получим 80 тысяч – а это значит, что лимит количества поющих фанатов достигнут.

Ответом на данную проблему моделирования является S-образная кривая – самая эффективная и универсальная математическая модель роста. Для того чтобы получить такую кривую, нам нужны всего два условия. Первое – такое же, как и для составления геометрической прогрессии: каждого поющего болельщика подхватывает другой болельщик, который до этого не пел. Затем отметим, что количество фанатов ограниченно: каждый болельщик может начать петь только один раз. Объединив эти два условия, мы получим S-образную кривую роста (см. рисунок 10.1)[113]. В самом начале рост будет медленным, однако он будет происходить в геометрической прогрессии.

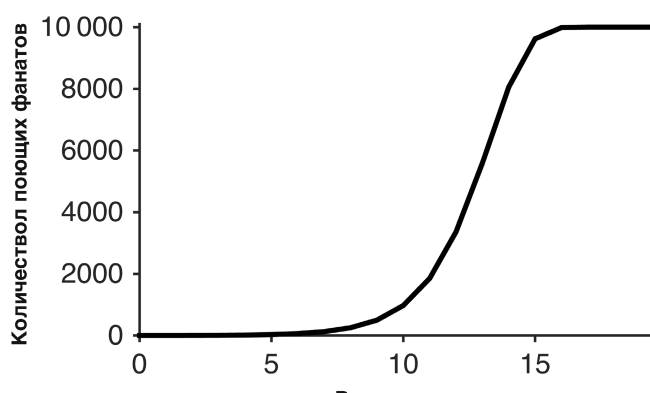
Рисунок 10.1. Постепенное увеличение количества поющих болельщиков через социальное заражение.

Количество поющих фанатов в каждом «раунде» увеличивается вдвое. Как только пением охватывается половина стадиона, рост снова замедляется и показатель в итоге стабилизируется на отметке, когда поют абсолютно все. Нужно всего 16 раундов, чтобы чант подхватили 10 тысяч фанатов.