§ 66. Построение четвертой пропорциональной

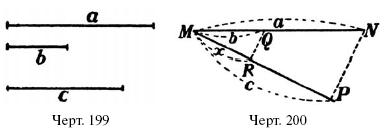
На практике приходится нередко отыскивать отрезок такой длины, чтобы вместе с тремя данными отрезками могла быть составлена пропорция. Пусть, например, даны три отрезка а, b и с (черт. 199) и требуется отыскать четвертый отрезок х такой длины, чтобы возможна была пропорция:

а: b = с: х.

Задача эта решается так. На прямой линии (черт. 200) откладывают от точки М отрезки а и b. Под произвольным углом к а от точки М проводят прямую, на которой откладывают отрезок с. Концы N и Р отрезков а и с соединяют прямой и через конец Q отрезка b проводят QR параллельно NP. Отрезок MR и есть четвертая пропорциональная х, потому что

а: b = с: х.

Решение подобных задач называется «построением 4-й пропорциональной».

а: b = с: х.

Повторительные вопросы

Что значит: «построить 4-ую пропорциональную»? – Какие вы знаете способы ее построения?

Применения

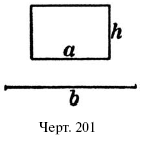
79. Прямоугольник со сторонами а и h(черт. 201) превратить в равновеликий прямоугольник с основанием b.

Р е ш е н и е. Надо начертить прямоугольник с основанием b и такой высотой х, чтобы bх = ax

Из последнего равенства вытекает пропорция b/a = h/x.

Следовательно, искомая высота х есть 4-я пропорциональная к a, h и b. Построив; ее по указанному раньше способу, мы сможем начертить и искомый прямо угольник.

80. Начертить прямоугольник с высотою b, равновеликий треугольнику с основанием а и высотою h.

Р е ш е н и е сводится к нахождению основания прямоугольника такой длины x, чтобы bх = bx = ah/2., т. е.,

чтобы x: a/2 = h: b

Значит, отрезок х есть 4-я пропорциональная к,a/2.h и b

81. Средняя линия трапеции p, высота – q. Построить равновеликий ей прямоугольник со стороною b.

Р е ш е н и е. Прямоугольник легко можно построить, если найдена будет его другая сторона х такой длины, что bx= pq, и следовательно х : р = д : b. Значит, х есть 4-я пропорциональная к р, q и b.