§ 90. Шар. Его объем и поверхность

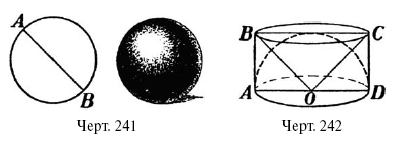
We use cookies. Read the Privacy and Cookie Policy

Шаром называется тело, которое можно представить себе образовавшимся от вращения полукруга около его диаметра (черт. 241). Все точки поверхности шара одинаково удалены от одной точки, называемой ц е н т р о м шара. Прямая, соединяющая центр шара с какой-нибудь точкой его поверхности, называется радиусом шара. Всякая прямая, соединяющая две точки его поверхности и проходящая через центр, называется д и а м е т р о м шара. Чтобы установить правило вычисления объема шара вообразим, что около полушара (черт. 242) описан цилиндр ABCD. Кроме того, вообразим себе конус, вершина которого в центре шара, а основание – совпадает с верхним основанием цилиндра.

Проведем теперь какую-нибудь плоскость, пересекающую все три тела параллельно основаниям цилиндра; эта плоскость MN(черт. 243) рассечет каждое из трех тел по кругу. Радиус круга, по которому рассечется цилиндр, есть PZ, полушар – PS, а конус – PK. Проведя радиус OSшара, имеем по теореме Пифагора [OS]2= [OP]2+ [PS]2.

Обозначим радиус основания цилиндра через R(он равен радиусу шара); радиус сечения полушара PSчерез h, радиус сечения конуса – через k. Тогда OS= OR= R; OP= PK= k(потому что противолежащие углы = 45°); PS= h. Написанное выше представим в виде

R2= k2+ h2.

Умножив все члены равенства на, имеем

R2= k2+ h2.

Равенство это означает, что площадь сечения нашего цилиндра [R2] равна площади сечения конуса [k2], сложенной с площадью сечения полушара [h2], лежащих в той же плоскости. Это справедливо для любой плоскости, пересекающей наши три тела параллельно основаниям цилиндра.

Представим себе теперь, что мы провели чрезвычайно много таких плоскостей в незначительном расстоянии Н друг от друга. Назовем эти плоскости номерами: № 1, № 2, № 3 и т. д. Они разрежут наши три тела на множество весьма тонких слоев, которые можно принять за цилиндры с высотою H. Для плоскости № 1, № 2, № 3 и т. д. мы будем иметь следующие объемы лежащих на них слоев:

№ 1. . . . . ?R2H = ?k12H + ?h12H

№ 2. . . . . ?R2H = ?k22H + ?h22H

№ 3. . . . . ?R2H = ?k32H + ?h32H

№ 4. . . . . . . . . . . . . . .

Сложив эти равенства почленно, мы получим в сумме первого столбца объем цилиндра Vц; в сумме второго столбца – все слои конуса,[13] т. е. его объем Vк, а в сумме третьего столбца – все слои полушара, т. е. его объем Vпш. Короче говоря, мы устанавливаем, что Vц = Vк + Vпш.

Так как объем цилиндра vц= ?R2? R= ?R3, а объем конуса 1/3?R2? R = 1/3?R3, то полученное сейчас равенство можно представить в виде ?R3= 1/3?R3+ Vпш, откуда объем полушара V = ?R3– 1/3?R3 =2/3?R3, а объем полного шара V = 4/3?R3.

Если бы мы пожелали выразить объем шара через диаметр, следовало бы только в этой формуле заменить R через d/2, где d – диаметр. Получим V = 4/3? d3/8= 1/6?d3

Зная формулу для вычисления объема шара, можно вывести правило вычисления его поверхности.

Для этого вообразим, что шар составлен из большого числа весьма узких пирамид, сходящихся вершинами в центре шара.

Объем одной такой пирамиды равен 1/3 площади ее основания, умноженной на ее высоту. Так как эти пирамиды чрезвычайно узки (мы можем представить их себе сколь угодно узкими), то за площадь Sих основания можно принять соответствующий участок а поверхности шара, а за высоту – радиус шара R. Тогда объемы наших пирамид выразятся последовательно через

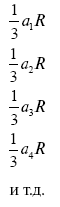
Сложив объемы всех этих пирамид и вынеси за скобку 1/3 R, получим, что объем V шара равен

v= 1/3R [a1 + a2 + a3 + a4 + и т. д.].

Но то, что в скобках, есть сумма всех участков шаровой поверхности, т. е. полная поверхность Sшара. Значит, v = 1/3RS.

Мы узнали, следовательно, что

о б ъ е м ш а р а р а в е н п р о и з в е д е н и ю т р е т и е г о р а д и у с а н а п о в е р х н о с т ь.

Отсюда выводим, что поверхность шара

S = V:1/3R = 3V/R

А так как мы уже узнали раньше, что v = 4/3?R3, то поверхность шара S = 3 ? 4/3?R3: 4?R2

Другими словами: п о в е р х н о с т ь ш а р а р а в н а у ч е т в е р е н н о й п л о щ а д и к р у г а т о г о ж е р а д и у с а.

Повторительные вопросы

Какое тело называется шаром? – Что называется центром шара, радиусом, диаметром? – Как вычислить поверхность и объем шара, если известен его радиус? – Если известен его диаметр? – Как высказать эти соотношения словесно?

Применения

123. Сколько весит оболочка воздушного шара диаметром 15 метров? Кв. м. оболочки весит 300 граммов.

Р е ш е н и е. Поверхность этого шара = 4 ? 1/4 ? ? ? 152 = 710 кв. м, а следрвательно, вес 210 кг.

124. Сколько свинцовых дробинок в 3 мм диаметром идет на 1 кг?

Р е ш е н и е. 1 кг свинца занимает объем 1000/11,3= 88,5 куб. см. Объем одной дробинки = 1/6 ? ? ? 0,33= 0,014 куб. см. Следовательно, на 1 кг идет 88,5/0,014 = 6300 дробинок указанного диаметра.

125. Диаметр Марса вдвое меньше земного. Во сколько раз поверхность и этой планеты меньше, чем Земли?

Р е ш е н и е. Поверхности шаров относятся как квадраты диаметров, а объемы, – как кубы диаметров. Поэтому поверхность Марса меньше земной в 4 раза, а объем меньше земного в 8 раз.

126. «При обыкновенном дожде вес капель не превышает 0,065 грамма. Визнер на острове Яве во время сильнейшего дождя определил средний вес капель в 0,16 грамма» (К л о с со в с к и й, «Основы метеорологии»). – Определить соответствующие этим данным поперечники дождевых капель, считая их форму шарообразною.

Р е ш е н и е. 0,065 грамма воды занимают 0,065 куб. сантиметра или 65 куб. миллиметров. Диаметр шара такого объема получаем из уравнения

1/6 ? ? ? x3=65, где x – диаметр в миллиметрах. Отсюда

Итак, крупная дождевая капля имеет в ширину полсантиметра. Диаметр самых больших измеренных капель (вес 0,16 грамма) равен 6,7 миллиметра.

127. Яблоко при печении сморщивается. На что это указывает?

Р е ш е н и е. На то, что объем яблока при печении уменьшается, кожура же сохраняет прежние размеры. Сделаем примерный расчет: вычислим какой избыток кожуры получается, когда яблоко диаметром 8 см уменьшается (вследствие потери воды при нагревании) на 4 миллиметра по диаметру. 4? ? 402– 4? ? 382= 4? [402– 382] = 4? ? 78 ? 2 = 2000 кв. мм, или 20 кв. см. Следовательно, общая поверхность всех морщин печеного яблока, при указанных размерах, равна 20 кв. см.