§ 58. Средняя линия трапеции

Предварительные упражнения

На черт. 161 прямые АВ и CD параллельны. Прямая KLпроведена через середину О отрезка EF. Докажите, что треугольники КОЕ и FOL равны.

В четырехугольнике AFED (черт. 155) сторона AF-DEи параллельна ей. Докажите, что этот четырехугольник есть параллелограмм.

С р е д н е й л и н и е й трапеции называется прямая, соединяющая середины ее непараллельных сторон (черт. 162). Этот отрезок обладает следующим свойством:

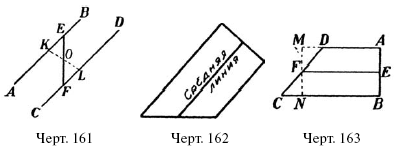
с р е д н я я л и н и я т р а п е ц и и р а в н а п о л у с у м м е е е о с н о в а н и й.

Удостовериться в этом можно так. Пусть в трапеции ABCD (черт. 163) прямая EF есть средняя линия, т. е. соединяет середины непараллельных сторон АВ и DC. Проведем через точку F прямую, параллельную АВ и продолжим AD до пересечения с сейчас проведенной линией. Треугольники FDM и FNCравны (УСУ), следовательно, MD = NC. Четырехугольник EBNF есть параллелограмм (EB= l/2AB; FN = 1/2MN; AB-=MN; значит, ЕВ равно и параллельно FN и т. д.); поэтому EF= BN. Точно так же EF= AM. Зная это, пишем:

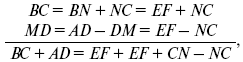
а откуда:

EF = BC + AD/2

Мы убедились, что во всякой трапеции средняя линия равна полусумме ее оснований. Вспомнив, что площадь трапеции равна полусумме ее оснований, умноженной на ее высоту, мы можем высказать следующим образом правило вычисления площади трапеции:

п л о щ а д ь т р а п е ц и и р а в н а е е с р е д н е й л и н и и, у м н о ж е н н о й н а в ы с о т у.

Повторительные вопросы к §§ 57 и 58

Что называется средней линией треугольника? – Каким свойством она обладает? – Как разделить данный отрезок на несколько равных частей? – Начертите какой-нибудь отрезок и разделите его на 3 равные части. – Разделите взятый вами отрезок на 7 равных частей. – Что называется средней линией трапеции? – Каким свойством она обладает? – Как можно вычислить площадь трапеции, если известны ее высота и средняя линии?

Применения

66. Фигура АВCD (черт. 164) ограничена прямой AD, двумя перпендикулярами АВ и CDи кривой ВС. Чтобы определить ее площадь, отрезок ADразделен на 5 равных частей, и из середины этих отрезков 1, 2, 3, 4, 5 восстановлены перпендикуляры к AD. Длина отрезка AD= 80 см; длины перпендикуляров: в точке 1 – 28 см, в 2 – 31 см, в.3 – 31,5 см, в 4 -32 см, в 5 – 34 см. Найти площадь АВСD.

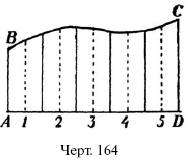
Р е ш е н и е. Площадь первой слева полосы = 28 16 = = 448 кв. см, второй – 31 16 = = 496 кв. см, третьей – 31,5 16 = = 504кв. см, четвертой – 32 16 = 512 кв. см, пятой – 34 16 = 544 кв. см. Искомая площадь = 2 500 кв. см.