§ 52. Катет против угла в 30°

Предварительное упражнение

Равносторонний треугольник разбит равноделящей одного из углов на два треугольника. Определить их углы.

уг. D= 60°; а так как и уг. ABD= 60°, то треугольник ABD– равносторонний, и следовательно, AD= АВ. Но АС = 1/2 АD (почему?); отсюда АС = 1/2 АВ.

Итак, мы убедились, что

к а т е т п р о т и в у г л а в 30° р а в е н п о л о в и н е г и п о т е н у з ы.

Применения

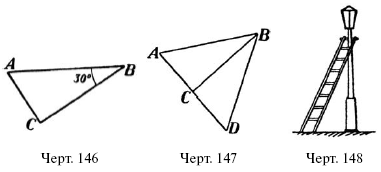
58. Лестница длиною 6 м приставлена к фонарному столбу под углом 30° к нему (черт 148). Каково расстояние от основания лестницы до основания фонаря?

Р е ш е н и е. Так как катет против 30° равен половине гипотенузы, то искомое расстояние = 3 м.

59. Длина стропильной ноги АС (черт. 137) вдвое больше высоты ADстропильной фермы. Определить угол наклона этой кровли к горизонту.

Р е ш е н и е. Искомый угол СAD = 30°, так как только при таком условии CD равно половине АС.

Пусть у нас имеется прямоугольный треугольник (черт. 146) ABC, один угол которого, именно В, равен 30°. Перегнем мысленно треугольник по катету ВС. Тогда займет положение ВСD (черт. 147), при чем CD составит продолжение АС, потому что уг. ВСD + ВСА = развернутому. Уг. СВD = уг. ABC= 30°; значит, уг. А = 60°;