Приложение 3

Площадь треугольника равна половине произведения его основания на высоту, проведенную к основанию. У треугольника TBC основание BC равно 2а, а высота ТА равна с. Следовательно, площадь треугольника равна с ? а. Мы хотим показать, что если квадрат высоты пирамиды h² равен площади ее треугольной стороны s ? a, то s/a равно золотому сечению.

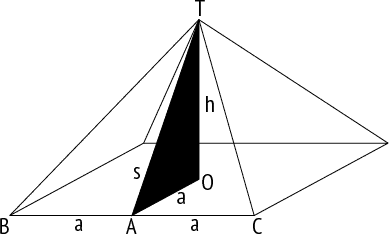
Дано, что

h² = s? a.

Применив теорему Пифагора к прямоугольному треугольнику TOA, получаем

s² = h² + a².

Теперь подставим значение h² из первого равенства и получим

s² = s? a + a².

Разделим обе части на a² и получим

(s/a)² = (s/a)+ 1.

Иными словами, если мы обозначим s/a как x, у нас получится квадратное уравнение

x² = x+ 1.

В главе 4 показано, что именно это уравнение и описывает золотое сечение.