Пифагоровы Фибоначчи

Как ни странно, числа Фибоначчи можно связать даже с пифагоровыми тройками. Как вы, наверное, помните, пифагоровы тройки – это тройки чисел, которые могут служить длинами сторон прямоугольного треугольника (в частности, это числа 3, 4, 5). Возьмите любые четыре последовательных числа Фибонанччи, ну, скажем, 1, 2, 3, 5. Произведение внешних – то есть первого и четвертого – равно 5, удвоенное произведение внутренних – то есть второго и третьего – равно 12, сумма квадратов внутренних чисел 2² + 3² = 13 – и это и будут три стороны пифагорейского треугольника (5² + 12² = 13²). Но это еще не все! Обратите внимание, что третье число – 13 – само по себе число Фибоначчи! Это свойство обнаружил математик Чарльз Райн.

Учитывая, сколько чудес таят в себе числа Фибоначчи (а вскоре мы познакомимся со множеством других их секретов), не стоит удивляться, что математики давно ищут эффективный метод вычисления произвольного члена последовательности F_n для любого n. В принципе это не так уж сложно: если нам нужно сотое число, надо сложить девяносто восьмое и девяносто девятое, однако это все равно означает, что сначала надо вычислить все члены последовательности до девяносто девятого, а это несколько утомительно. Как писал покойный юморист Джордж Бернс в своей книге «Как прожить сто лет и больше» (George Burns. How to Live to Be 100 or More): «Как прожить сто лет и больше? Кое над чем придется потрудиться. Главное – обязательно дотянуть до девяносто девяти».

В середине XIX века французский математик Жак-Филипп-Мари Бине (1786–1856) заново открыл формулу, которую, по всей видимости, еще в XVIII веке знали и самый плодовитый математик в истории человечества Леонард Эйлер (1707–1783), и французский математик Абрахам де Муавр (1667–1754). По этой формуле можно найти значение любого числа Фибоначчи Fn, если известно его место в последовательности – n. Так вот, эта формула Бине целиком опирается на золотое сечение.

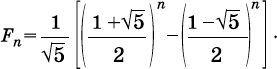
На первый взгляд это не формула, а сущий кошмар: не очевидно даже, что при подстановке в нее различных значений n получатся целые числа, а ведь все члены последовательности Фибоначчи – целые. Поскольку мы уже знаем, что числа Фибоначчи тесно связаны с золотым сечением, нас, пожалуй, несколько обнадежит, когда мы поймем, что первый член в скобках – это, в сущности, золотое сечение в степени n, ?ⁿ, а второй – (–1/?) ⁿ. (Вспомним, что выше мы обсуждали, что отрицательный корень квадратного уравнения, определяющего число ?, равен – 1/?). Вооружившись простым инженерным карманным калькулятором, можно самостоятельно ввести несколько значений n и убедиться, что формула Бине дает числа Фибоначчи в точности. При достаточно больших значениях n второй член в скобках становится очень маленьким, так что можно просто считать, что F_n – это ближайшее целое число к ?ⁿ/?5. Например, при n = 10, ?ⁿ/?5 = 55,0036, а десятое число Фибоначчи и есть 55.

Можно задаться вопросом – так, забавы ради, – существует ли число Фибоначчи, состоящее ровно из 666 цифр. Математик и писатель Клиффорд А. Пиковер называет числа, связанные с 666, «апокалиптическими». Он обнаружил, что число Фибоначчи номер 3184 состоит из 666 знаков.

Итак, стоило лишь открыть числа Фибоначчи, и они, как по волшебству, стали возникать тот тут, то там, в том числе и в живой природе. Вот и ботаника дарит нам несколько интереснейших примеров.