§ 3. Алгоритм Евклида
§ 3. Алгоритм Евклида
Вновь вернемся к нашим дробям а/b. Если а > b, то дробь является числом, большим 1, и мы часто разделяем ее на целую часть и правильную дробь, меньшую единицы.
Примеры. Мы пишем
32/5 = 6 + 2/5 = 6 2/5, 63/7 = 9 + 0/7 = 9.
В общем случае мы используем деление с остатком
чисел а и b (a ? b), а именно:
a = qb + r, где 0 ? r ? b—1. (4.3.1)
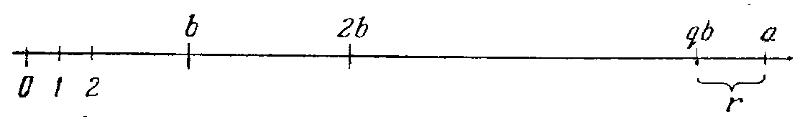
Рис. 14.
Очевидно, что это всегда возможно. Действительно, рассмотрим числа 0, 1, 2… на числовой прямой (рис. 14). Где-то на этой прямой расположено число а. Начиная от точки 0 станем отмечать точки b, 2b, Зb и т. д. до точки qb такой, что qb не больше, чем а, в то время как (q + 1)b уже больше а. Расстояние от точки qb до точки а и есть r. Мы называем число r остатком при делении (4.3.1), a q — частным. Это частное q встречается столь часто, что имеется специальный символ для его обозначения:
q = [a/b].
Этот символ обозначает наибольшее целое число, не превосходящее числа а/b. Для примеров, приведенных выше, получим
[32/5] = 6, [63/7] = 9.
В предыдущем разделе мы исследовали наибольший общий делитель двух натуральных чисел а и b:
d0 = D(a, b). (4.3.2)
Чтобы найти число d0, мы полагали, что мы знаем разложения чисел а и b на простые множители. Однако нахождение таких разложений может оказаться очень трудным занятием для больших чисел. Существует совсем другой метод для нахождения наибольшего общего делителя, который не использует подобных разложений. Он основан на следующем:
Если a = qb + r, где 0 ? r ? b—1, то
D(a, b) = d = D(r, b). (4.3.3)
Доказательство. Запишем
d0 = D(a, b), d1 = D(r, b).
Таким образом, доказательство соотношения (4.3.3) означает доказательство того, что d0 = d1. Любой общий делитель чисел а и b также делит число
r = а — qb.
Следовательно, число r делится на d0.
Так как число d0 является делителем как числа r, так и числа b, то оно должно делить и число d1 = D(b, r); отсюда d1 ? d0. С другой стороны, в соответствии с соотношением (4.3.1) любой общий делитель чисел r и b делит число а, откуда число d1 делит число а. Так как число d1 делит также и число b, то оно должно делить и число d0 = D(a, b), следовательно, d0 ? d1. Из сказанного следует, что d0 = d1.
Пример. 1066 = 5 • 200 + 66; следовательно, (1066, 200) = (66, 200).
Этот результат, сформулированный в утверждении (4.3.3), дает нам простой метод вычисления наибольшего общего делителя двух чисел. Вместо поисков наибольшего общего делителя чисел а и b достаточно найти наибольший общий делитель чисел r и b. Эта задача более проста, так как число r меньше, чем каждое из чисел а и b. Чтобы найти наибольший общий делитель чисел r и b, мы вновь воспользуемся тем же методом и разделим число b на r:
b = q1r + r1,
где r1 меньше каждого из чисел b и r. В соответствии с правилом (4.3.3) мы получаем
d0 = D(a, b) = D(b, r) = D(r, r1).
Далее, таким же способом обращаемся с числами r и г1 и т. д. В результате получаем последовательность пар чисел, каждая из которых имеет один и тот же наибольший общий делитель:
d0 = D(a, b) = D(b, r) = D(r, r1) = D(r1, r2) =… (4.3.4)
Так как остатки постоянно уменьшаются, то эта последовательность должна закончиться после получения остатка rk+1 = 0. Это происходит при делении
rk-1 = qk+1rk + 0,
т. е. число rk делит число rk-1. Тогда
D(rk-1, rk) = rk,
и из (4.3.4) видим, что
d0 = D(а, b) = rk.
Другими словами, число d0 равно первому из остатков, который делит предшествующий ему остаток.
Пример. Найдем наибольший общий делитель чисел 1970 и 1066. Когда мы разделим одно число на другое и продолжим этот процесс дальше, как было выше рассказано, то найдем
1970 = 1 • 1066 + 904,
1066 = 1 • 904 + 162,
904 = 5 • 162 + 94,
162 = 1 • 94 + 68,
94 = 1 • 68 + 26,
68 = 2 • 26 + 16,
26 = 1 • 16+ 10,
16 = 1 • 10 + 6,
10 = 1 • 6 + 4,
6 = 1 • 4 + 2,
4 = 2 • 2 + 0.
Следовательно, (1970, 1066) = 2.
Этот метод нахождения наибольшего общего делителя двух чисел называется алгоритмом Евклида, так как первое его описание содержится в «Началах» Евклида. Этот метод очень удобен для применения в вычислительных машинах.
Система задач 4.3.
1. Решите задачу 1 § 1 (с. 49), используя алгоритм Евклида.
2. Найдите наибольший общий делитель для каждой из пяти первых пар дружественных чисел. Сравните результаты с результатами, полученными с помощью разложения на простые множители.
3. Каким количеством нулей заканчивается число
n! = 1 • 2 • 3 •… • n?
Сверьте свой результат с таблицей факториалов.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОКЧитайте также
Глава 3 Конкуренты Евклида
Глава 3 Конкуренты Евклида На протяжении веков пятый постулат вызывал обильные комментарии и критику в трудах самых известных геометров. Многие из них были убеждены, что этот постулат можно доказать с помощью других постулатов, и сосредоточили свои усилия на поиске
Глава 1 До Евклида — доисторические времена
Глава 1 До Евклида — доисторические времена Истинное начало этой истории теряется во мгле времен апокрифических.Где, как и когда начиналась геометрия… Где, как и когда обрела она законченную форму и заслужила право называться наукой… Кто был тот неведомый, первый,