§ 4. Возведение сравнений в степень

§ 4. Возведение сравнений в степень

Предположим вновь, что имеется сравнение

a ? b (mod m).

Как мы только что видели, можно умножить это сравнение на себя, получив

а² ? b² (mod m).

Вообще можно, умножив это сравнение на себя нужное количество раз, получить

aⁿ ? bⁿ (mod m)

для любого целого положительного числа m.

Пример. Из сравнения

8 ? -3 (mod 11)

после возведения в квадрат следует сравнение

64 ? 9 (mod 11),

а после возведения в куб получаем сравнение

512 ? -27 (mod 11).

Многие результаты теории сравнений связаны с остатками высоких степеней чисел, поэтому покажем, как можно продолжить процесс возведения в степень. Предположим, например, что мы хотим найти остаток сравнения

3⁸⁹ (mod 7).

Одним из путей для выполнения этого является повторное возведение в квадрат. Мы находим:

9 = 3² ? 2 (mod 7),

3⁴ ? 4,

3⁸ ? 16 ? 2,

3⁶⁴ ? 4 (mod 7).

Так как

89 = 64 + 16 + 8 + 1 = 2⁶ + 2⁴ + 2³ + 1,

то отсюда следует, что

3⁸⁹ = 3⁶⁴ • З¹⁶ • З⁸ • 3 = 4 • 4 • 2 • 3 ? 5 (mod 7).

Таким образом, остаток (по модулю 7) есть 5, или, говоря другими словами, в соответствии с изложенным в § 2, последняя цифра числа З⁸⁹, записанного в системе счисления при основании 7, равна 5.

В действительности, для того чтобы найти этот остаток, мы записали показатель степени

89 = 2⁶ + 2⁴ + 2³ + 1 = (1, 0, 1, 1, 0, 0, 1)

в двоичной системе счисления. Повторным возведением в квадрат мы нашли остатки (по модулю 7) тех степеней числа 89, которые сами являются степенями числа 2:

1, 2, 4, 8, 16, 32, 64.

Соответствующий метод можно использовать для любых других оснований. Однако в частном случае бывает возможность упростить вычисление, если заметить особенности этого случая. Например, в случае, разобранном выше, мы можем отметить, что

3³ ? -1 (mod 7),

З⁶ ? 1 (mod 7),

откуда заключаем, что

3⁸⁴ = (3⁶)¹⁴ ? 1 (mod7).

Поэтому

3⁸⁹ = 3⁸⁴ • 3³ • 3² ? 1 • (-1) • 2 = -2 ? 5 (mod 7),

как и раньше.

В качестве другой иллюстрации сказанного можно рассмотреть числа Ферма, с которыми мы познакомились в § 3 гл. 2:

F_n = 2^2?+1.

Первые пять чисел Ферма таковы:

F₀ = 3, F₁ = 5, F₂ = 17, F₃ = 257, F₄ = 65537.

Отсюда можно высказать предположение:

десятичная запись всех чисел Ферма, за исключением F₀ и F₁ оканчивается цифрой 7.

Докажем с помощью сравнений, что это действительно так. Очевидно, что оно равносильно утверждению, что числа

2^2?, n = 2, 3…

оканчиваются цифрой 6. Это можно доказать по индукции. Заметим, что

2^2? = 16 ? 6 (mod 10),

2^2? = 256 ? 6 (mod 10),

2^2?4 = 65536 ? 6 (mod 10),

Более того, если мы возводим в квадрат число 2^2?k, то результатом будет число

Предположим, что для некоторого значения t

;

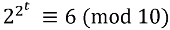возводя в квадрат это сравнение, мы находим, что

,

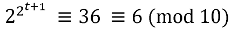что и требовалось.