§ 3. Сравнение систем счисления

§ 3. Сравнение систем счисления

Американское общество сторонников двенадцатеричной системы предложило изменить нашу десятеричную систему на более эффективную и удобную, как они думают, систему с основанием 12. Те, кто предлагает эту систему, указывают, что было бы выгоднее иметь систему с основанием, делящимся на числа 2, 3, 4 и 6, так как процесс деления на эти часто встречающиеся делители упрощается. Доводы такого типа привели бы нас к шестидесятеричной системе, основание которой, число 60, делится на числа

2, 3, 4, 5, 6, 10, 12, 15, 20, 30.

В ряде стран многие вещи все еще считают дюжинами и гроссами (т. е. дюжинами дюжин) и естественно, что для них двенадцатеричная система является вполне возможной. Для перехода в двенадцатеричную систему нужно было бы ввести двенадцать новых символов, что потребует для их разработки столь же много усилий, сколько потребовалось для создания десятеричной системы. Некоторые энтузиасты считают, что необходимо ввести новые символы лишь для 10 и 11, но такой способ не учитывает неудобств, возникающих в период перехода: никто не будет понимать, например, означает ли запись 325

3 • 10² + 2 • 10 + 5 = 325

или

3 • 12² + 2 • 12 + 5 = 461.

Для того чтобы получить представление о том, как меняется количество знаков в числе в зависимости от системы счисления, возьмем число

10ⁿ — 1 = 99… 9 (n раз) = N (6.3.1)

в десятеричной системе. Это самое большое число с n знаками. Чтобы найти m — количество знаков при записи этого числа при основании b — мы должны определить m как целое число, для которого выполняются неравенства

b^m > 10ⁿ — 1 ? b^m-1. (6.3.2)

Это условие может быть также записано в виде

b^m ? 10ⁿ > b^m-1.

Возьмем логарифмы этих трех чисел. Вспомнив, что lg 10 = 1, получим, что

m lg b ? n > (m — 1) lg b.

В свою очередь эти неравенства могут быть переписаны в виде

m ? n/lg b > (m — 1); (6.3.3)

таким образом, m является первым целым числом не меньшим, чем n/lg b.

Отсюда делаем вывод, что, грубо говоря, m — новое количество знаков, может быть получено делением числа n на lg b.

Примеры. Пусть вновь n будет количеством знаков числа в десятичной системе. Для b = 2 мы имеем: lg 2 = 0,30103, таким образом, количество цифр в двоичной системе приблизительно равно 3,32 n. Когда b = 60, мы имеем: lg 60 = 1,778, отсюда количество знаков приблизительно равно 0,56 n, т. е. немного больше, чем половина количества знаков в десятичной системе.

Ясно, что короткими числами удобнее оперировать. Но, с другой стороны, числа при больших основаниях имеют ряд недостатков. Во-первых, нужно иметь названия и обозначения для b различных цифр, чего обычно нет для больших значений b. Например, в вавилонской шестидесятеричной системе считали единицы до 60, группируя их по десять, как показано на рис. 15.

Рис. 15.

Это означает в действительности, что эта система расщеплялась на подсистемы с десятеричной записью. Аналогичная ситуация существует в двадцатеричной системе народа майя. Здесь цифры до 20 считались пятерками, как показано на рис. 16.

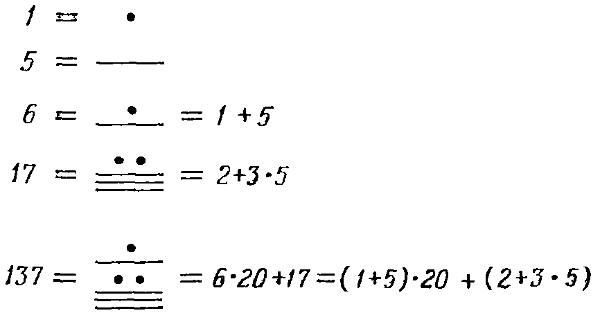
Рис. 16.

Вторым и гораздо большим недостатком является трудность, возникающая при попытках вычислений с помощью обычных методов. Когда мы выполняем действие умножения, то пользуемся знанием наизусть таблицы умножения, т. е. знанием произведений всех десяти цифр. Эта таблица Пифагора, как ее называют во многих странах, вдалбливалась нам в течение первых школьных лет, и знаем мы ее почти автоматически. Это знание не столь тривиально, как мы склонны думать. Из средневековых арифметических манускриптов ясно видно, что умножение было на грани высшей математики, а деление больших чисел было в действительности редким искусством. Но можно привести и гораздо более поздние примеры.

Самюэль Пепис, известный благодаря своему дневнику, был в возрасте около тридцати лет и служил клерком канцелярии лорда-хранителя печати, когда летом 1662 года он решил, что он должен знать кое-что из математики, по крайней мере основы арифметики, чтобы самостоятельно проверять счета. Заметим, что он тогда уже получил степени бакалавра и магистра в Кембридже. В то время было довольно обычным, что хорошо образованный английский джентльмен совершенно не владеет повседневными расчетами; эти расчеты могли перепоручаться младшим счетоводам.

4 июля 1662 года Пепис записывает в своем дневнике: «Вскоре придет мистер Купер, помощник капитана на „Ройял Чарльз", у которого я собираюсь учиться математике, и сегодня мы начнем; он очень способный человек, я полагаю, что не найдется дела, которое способно полностью его удовлетворить. После часа занятий арифметикой (я пытался выучить таблицу умножения) мы расстались с ним до завтра».

Каждый день и рано утром и поздно вечером Пепис учил проклятую таблицу умножения, с трудом продвигаясь вперед при поддержке своего моряка-учителя. Например, 9 июля он записывает: «Встал в четыре часа утра и снова упорно учу таблицу умножения, которая для меня является главной трудностью арифметики». Так продолжалось несколько дней, пока 11 июля он смог записать: «Встал в четыре часа утра и упорно работал над таблицей умножения, которой я теперь почти овладел». Пепис хорошо использовал полученные с таким трудом знания во всех все более важных постах, на которые он назначался. Однако может показаться слишком быстрым его продвижение, когда вы узнаете, что он был избран членом знаменитой Британской академии наук — Королевского общества — спустя два с половиной года после того, как выучил таблицу умножения.

Мы привели эту историю, которая никоим образом не является уникальной, чтобы подчеркнуть: запоминание таблицы умножения в те дни не было обычным этапом математического знания. Таким образом, мы видим, что использование в нашей арифметике чисел с небольшим основанием дает ряд преимуществ, как механических, так и интеллектуальных. Например, когда основанием является число b = 3, то в таблице умножения

  | 0 1 2

  |________ 

0 | 0 0 0

1 | 0 1 2

2 | 0 2 (1,1)₃

существует только единственное нетривиальное умножение, а именно: 2 • 2 = 4 = (1, 1)₃.

Для b = 2 мы имеем совершенно тривиальную таблицу

  | 0 1

  |____

0 | 0 0

1 | 0 1

Система задач 6.3.

1. Доказать, что количество нетривиальных умножений цифр (получающееся отбрасыванием умножений на 0 и 1) в системе с основанием b равно 1/2 (b — 1) (b — 2).

2. Чему равна сумма всех элементов в таблице умножения? Проверьте для b = 10.