Мартышкин труд

Задача об обезьянах возникла, как вопрос статистической механики в теории вероятностей; впервые она была сформулирована в статье Эмиля Бореля «Статистическая механика и необратимость» (M?canique Statistique et Irr?versibilit?), опубликованной в 1913 г. Это теорема, которая утверждает, что обезьяна, случайным образом нажимающая на клавиши, напечатает полное собрание сочинений Шекспира, при условии что у нее будет достаточно времени. Конечно, «достаточно времени» может означать бесконечно долгое время. Английский физик сэр Артур Эддингтон был более великодушен в отношении случайности, когда его пригласили дать гиффордовскую лекцию в Эдинбургском университете в 1927 г.: «Если я дам своим пальцам вольно блуждать по клавишам печатной машинки, то «может» случиться так, что из этого моего опуса выйдет вразумительное предложение. Если бы армия обезьян безостановочно стучала по клавишам печатных машинок, то они могли бы написать все книги, хранящиеся в Британском музее»{90}.

Давайте пока не будем усложнять задачу. Давайте не будем ожидать библиотеки Британского музея, или полного собрания сочинений, или даже единственного сонета, а только одну строку «shall I compare thee to a summer's day?». Если обезьяна нажмет на клавиши s-h-a-l-l-I-c-o-m-p-a-r-e-t-h-e-e-t-o-a-s-u-m-m-e-r-s-d-a-y именно в таком порядке, мы наверняка сочтем это грандиозным совпадением. Какова вероятность такого события? В самом деле, весьма небольшая! У обезьяны шанс 25 к 1 напечатать первую букву в слове shall, если допустить, что клавиатура ограничена только строчными буквами английского алфавита. А поскольку каждое нажатие на клавишу относительно независимо от других{91}, число возможных вариантов того, что обезьяна напечатает первые 5 букв, равняется 26 ? 26 ? 26 ? 26 ? 26 = 11 881 376, или шанс 11 881 375 к 1. Но это шанс выполнить задачу с первой попытки. Бедному животному надо дать больше, чем только один шанс. Много больше. Рассмотрим вероятность невыполнения задачи с первой попытки. Она составит 1 – (1/26)⁵ ? 0,99999991583, т. е. близка к достоверности. После N попыток вероятность того, что она не нажмет клавиши в нужном порядке, составит (1 – (1/26)⁵)^N.

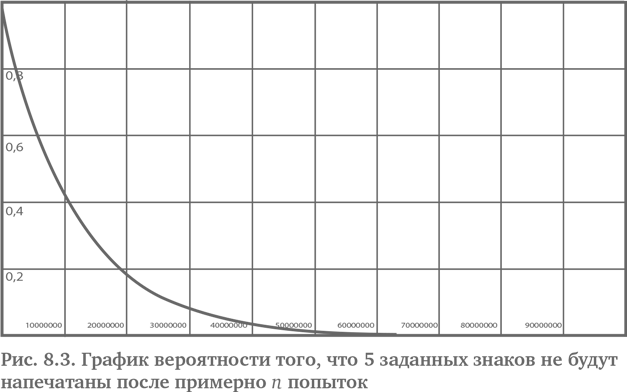
При N = 8 235 542 у нее будет шанс выше, чем 1 к 1, напечатать первое слово из шекспировского сонета. Рис. 8.3{92} показывает, как вероятность не напечатать слово shall приближается к нулю после примерно 50 млн попыток.

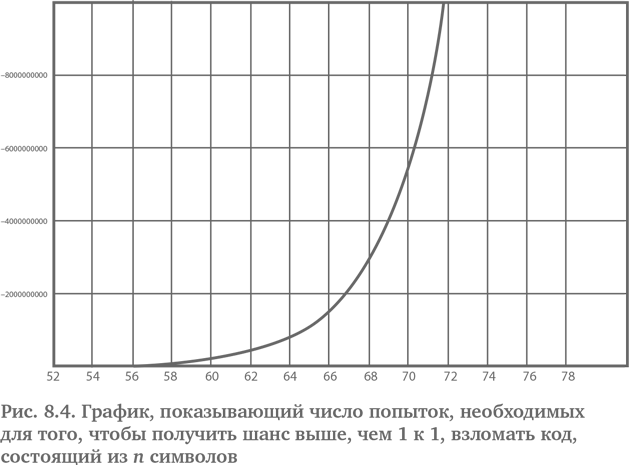
Попробуйте приложить это к парольной защите. Значит, компьютерная программа, которая подбирает буквы случайным образом, может легко взломать пароль, состоящий из 5 символов. В наши дни даже относительно слабый центральный процессор может перебрать 50 млн попыток меньше чем за 10 сек. Но если вы добавите всего один символ, то для того, чтобы иметь шанс подбора выше, чем 1 к 1, потребуется уже не менее 214 124 096 попыток. С каждым дополнительным символом (включая комбинации букв, чисел и символов или изменение регистра) сложность растет экспоненциально (см. рис. 8.4).

Вероятность случайного подбора первых 6 цифр ? с числовой клавиатуры – 0,000001, или шанс один на миллион. Существует шанс выше, чем 1 к 1, что одна из тысячи обезьян нажмет первые 6 цифр ?, если каждой из обезьян дать 1000 попыток. Возможно, ? – не такое уж особенное число. Конечно, мы берем только первые 6 цифр ?. Возьмем первые 100 цифр ?. Даже если каждая песчинка на Земле и каждая звезда во Вселенной станут случайным образом подбирать цифры до конца времен, вероятность написания ? до сотого знака практически не сдвинется с нуля. В 1913 г. Эмиль Борель предложил нам представить миллион обезьян, случайным образом стучащих по клавишам печатной машинки по 10 часов в день{93}.

Les contrema?tres illettr?s rassembleraient les feuilles noircies et les relieraient en volumes. Et au bout d'un an, ces volumes se trouveraient renfermer la copie exacte des livres de toute nature et de toutes langues conserv?s dans les plus riches biblioth?ques du monde.

(Неграмотные мастера собирают почерневшие листы и соединяют их в тома. По прошествии одного года эти тома будут содержать точные копии книг по какой угодно теме на всех языках, хранящихся в богатейших библиотеках мира.)

Сэр Джеймс Джинс написал в своей книге «Загадочная Вселенная»{94}:

Кажется, Хаксли сказал, что шесть обезьян, которых усадили бездумно тренькать по печатным машинкам миллионы миллионов лет, должны со временем написать все книги из Британского музея. Если бы мы рассмотрели последнюю страницу, напечатанную конкретной обезьяной, и обнаружили, что ей удалось в этом слепом тренькании набрать сонет Шекспира, мы бы справедливо сочли это событие выдающимся совпадением, но если бы мы пролистали все миллионы страниц, которые обезьяны извели за бессчетные миллионы лет, то могли бы быть уверены, что где-то среди них найдется еще один шекспировский сонет – плод слепой игры случая. Точно так же миллионы миллионов звезд, слепо скитающихся сквозь пространство миллионы миллионов лет, обязательно встретятся со всяческими случайностями и обязательно произведут некоторое конечное число планетарных систем через определенное время. И все же это число должно быть очень малым в сравнении с общим числом звезд на небе.

Задача об обезьянах была симулирована с помощью виртуальных обезьян. 4 августа 2004 г. компьютеры работали в качестве виртуальных обезьян, жмущих на клавиши в течение 42 162 500 000 миллиарда миллиардов обезьяно-лет, прежде чем смогли напечатать «VALENTINE. Cease toIdor: eFLP0FRjWK78aXzVOwm) – `;8.t»{95}. Изумительно, но первые 19 символов этой тарабарщины в точности воспроизводят первые 19 символов первой строки пьесы Шекспира «Два веронца»:

Valentine: Cease to persuade, my loving Proteus:

Я долго раздумывал над девятью заглавными буквами подряд, пока не сообразил, что на какое-то время оказался «случайно» зажат Caps Lock. Согласен, 42 квинтиллиона – это мегагромадное число, но то, что на набор этих 19 символов в определенном порядке ушло так много времени, не значит, что это не могло произойти много раньше. Надо признать: если бы такое удалось с первой попытки, то это было бы невообразимой причудой судьбы, но не чем-то невозможным. Неожиданное может происходить, и оно происходит. Возьмем совпадение ДНК. Есть ли в мире два не состоящих в родстве индивида, имеющих полностью совпадающие ДНК? Вероятность этого невообразимо мала, но все же отлична от нуля. На самом деле шансы всего лишь 1 на миллиард.