Две шестерки и рождение вероятности

Центральные понятия математической вероятности можно отследить уже в 1654 г. Зима в Париже была необыкновенно холодной. Даже Сена замерзла. Сообщалось, что парижане катались по реке на коньках, а на перекрестках горели костры, рядом с которыми священники раздавали беднякам хлеб. Экономика была задушена 30 годами религиозных войн в Европе, опустошившими французскую казну. Государство было вынуждено повысить налоги на рабочий класс, но бесчестные сборщики налогов мало что доносили до казны. На троне восседал Людовик XIV, а знать, освобожденная от налогообложения, накапливала ужасающе непомерные богатства. Не случайно праздные богачи открыто предавались азарту в игровых залах по всему Парижу{40}. Как не случайно и то, что нарождающаяся математическая теория вероятностей появилась именно тогда, в ту самую зиму 1654 г.

Несмотря на то что азартные игры известны с начала времен или по крайней мере с тех пор, когда троглодиты стали катать кости по полу своих пещер, к середине XVII в. они стали основным видом развлечений во Франции. Серьезной математической теории случайного не существовало, кроме грубых попыток, которые мы находим в ошибочных математических работах и книге Фра Лука Пачоли «Сумма» (Summa), опубликованной в 1494 г., – учебнике, в основном посвященном алгебре. К 1654 г. рукопись Кардано «Книга об азартных играх» вышла в свет с некоторыми подсказками по поводу того, сколько раз нужно бросить пару игральных костей, чтобы иметь шансы на комбинацию из двух шестерок выше, чем один к одному{41}.

Философ-математик Блез Паскаль прочел экземпляр «Книги об азартных играх» в поисках этого числа, но не поверил в приведенное решение. Он заболел и пролежал в постели весну и лето, ведя переписку со своим другом, юристом и математиком Пьером Ферма{42}. Вместе они пришли к выводу, что шансы выбросить две шестерки немного меньше, чем 1 к 1, при 24 попытках и немного больше при 25.

Паскаль знал, что «глаза змеи» (две единицы) и «товарные вагоны» (две шестерки) появляются очень редко, поскольку шанс их выбросить – 1 к 36, тогда как шанс выбросить семерку – 1 к 6 (рис. 5.1). Он понял, что проще будет вычислить шанс не выбросить две шестерки, т. е. 1 – 1/36 или 35/36. Он также понял, что каждый бросок не зависит от предыдущего и что вероятность двух независимых событий – это произведение вероятностей каждого из событий, а тогда вероятность не выбросить две шестерки за n бросков – (35/36)ⁿ. Он вычислил, что (35/36)²⁴ равняется 0,509, а (35/36)²⁵ равняется 0,494, и пришел к выводу, что шанс получить две шестерки за 24 броска немного ниже, чем 1 к 1, и немного выше, чем 1 к 1, за 25 бросков{43}.

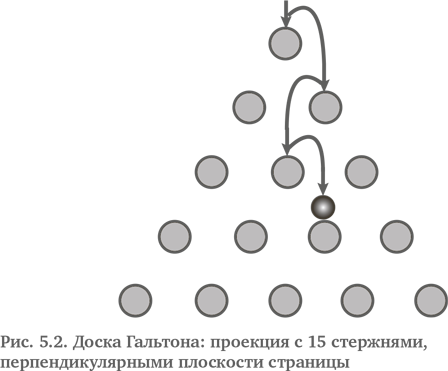
Основы учения о вероятности пришли из задачи об игральных костях и ей подобных. Внешний слой вероятностного или стохастического мира можно проиллюстрировать одной картинкой. Давайте поразмыслим о мире следующим образом: если на событие влияет некая причина, то шансы, что эта причина придаст направление возможному будущему событию, выше, чем один к одному. Если на событие не влияет никакая причина, то возможное будущее развитие события может пойти в том или ином направлении без предрасположенности к какому-либо конкретному исходу. Есть ли причина, нет ли ее – шансы выше, чем один к одному, оставляют открытой дверь для случайности или совпадения. На рис. 5.2 мы показываем это с помощью так называемой доски Гальтона в качестве модели.

Доска Гальтона моделирует события, определяемые объективной случайностью. На набор стержней бросают шарик таким образом, что шарик ударяется точно о середину верхней части стержня, при этом шансы, что шарик отскочит влево или вправо – точно 1 к 1. Если шарик отскакивает вправо, то он опускается на стержень, находящийся ниже, и либо снова ударяется точно о середину верхней его части, либо отклоняется в одну или другую сторону. В теории шарик может удариться точно о середину верхней части стержня. На практике, однако, этого никогда не происходит. Почему? Сначала мы должны задуматься: что значит «верхняя часть стержня»? Значит ли это верхнюю молекулу стали (если предположить, что стержни сделаны из стали)? Но ее не существует. Тогда на практике есть причины того, что шарик отклоняется в одну или другую сторону. Возможно, это малейший поток воздуха, через который должен пройти шарик, или малейшие колебания, проходящие через опоры стержней, или мельчайшая частичка пыли, оказавшаяся в месте соударения шарика и стержня. На практике есть сотни переменных, определяющих, в какую сторону отскочит шарик после столкновения со стержнем. Кроме того, следует учитывать микроскопические вмятины и упругость соударения.

Сэр Фрэнсис Гальтон, английский генетик, живший в XIX в., построил такую доску со штырями, расположенными в шахматном порядке – как точки на грани игральных костей с числом 5. Гальтон хотел показать, что физические явления движутся с попутным ветром случайности. В идеальной доске Гальтона, т. е. в такой, где шарик всегда попадает ровно в центр верхней части стержней, шарик отклоняется вправо или влево так, как если бы для выбора направления кто-то подбрасывал монетку. В реальности же бабочка, взмахнувшая крыльями над Тихим океаном, или корова, пукнувшая на кукурузном поле в Айдахо, могут определять этот выбор. Перед каждым соударением результат предыдущего – это забытое прошлое; шарик уже не помнит предыдущего исхода, а потому ведет себя так, как если бы ударился о первый стержень. И все же совокупный результат, похоже, учитывает историю всех предыдущих.

Давайте рассмотрим это с точки зрения математики. Предположим, что шарик ударяется о четыре ряда стержней на пути вниз. Шанс того, что шарик пойдет после каждого удара вправо или влево, – 1 к 1, в результате чего шарики формируют под стержнями кривую в форме колокола. Подсчет числа вариантов падения шариков это доказывает. Предположим, что ход снижения брошенного шарика записывается буквами L и R, означающими отскок влево и вправо соответственно. Тогда у нас будут следующие возможные исходы:

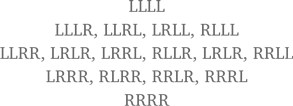
Вариантов с разными буквами больше, чем только с одной буквой, и, поскольку шансы того, что шарик пойдет влево или вправо, равны, есть тенденция к тому, что шарики будут чаще падать в сторону центра под верхним стержнем. Причина в том, что в результате серий, скажем 12 выборов L и R (как показано на рис. 5.3), существует больше серий с шестью L и шестью R, чем любого другого числа L и R.

В результате каждого столкновения со стержнями считаем падение шарика влево как –1, а вправо – как +1. После столкновения с 12 рядами стержней шарик оказывается в одной из 12 ячеек в нижней части доски.

Так, например, шарик в крайней левой ячейке на рис. 5.3 получает совокупное значение –12. Конечное положение каждого шарика представляет отдельное совокупное значение. Шарики демонстрируют тенденцию к тому, чтобы отклоняться в центр. Однако, хотя достаточно много шариков падают в два центральных слота, большее их число оказывается в остальных слотах.

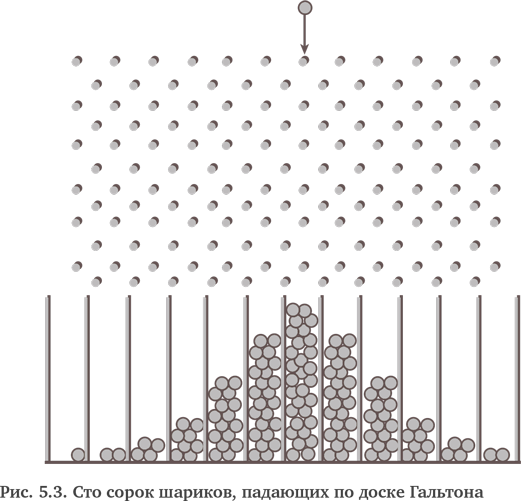
На рис. 5.3 набор шариков представляет конечное совокупное значение 140 испытаний: 31 шарик упал в пять слотов слева, 55 – в пять слотов справа и 54 – в два средних слота. Верно, что конечное положение каждого отдельного шарика ничего не говорит об истории его путешествия. Почти 60 % шариков упали вне двух центральных слотов. В общем, шарик, упавший на несколько рядов вниз и находящийся слева, может закончить свой путь справа, но так же верно и то, что, чем дальше он отклоняется влево, тем меньше у него шансов вернуться вправо.

Сегодня теория вероятностей развивается в двух направлениях: эмпирическом и абстрактном. Например, эмпирическим подходом будет использовать большие выборки, чтобы оценить вероятность, тогда как абстрактным подходом – задействовать научный принцип, чтобы зафиксировать вероятность через известные факты, такие как аргумент симметрии или физическая теория. Нам известна вероятность того, что идеальные игральные кости выпадут на 1 в силу кубической геометрии самих костей. Но вероятность выпадения 1 на обычных игральных костях может быть найдена посредством большого числа испытаний и записи числа испытаний, когда выпадает 1; эта вероятность может оказаться немного больше или меньше 1/6 – все-таки это реальные несовершенные кости.

Многое зависит от самой кости. Кости, которые входят в наборы для настольных игр, выполнены довольно грубо. Ятзи – игра в кости, появившаяся в 1950-е гг. В игре используется 5 кубиков. Если при броске все 5 костей дают одно и то же число, такая комбинация называется ятзи. Шансы выбросить ятзи – 1295 к 1.{44} Вы могли бы решить: чтобы выбросить такую комбинацию, потребуется 1296 попыток. Но если достаточно большое число людей по всему миру уделят игре хотя бы немного времени, то такая комбинация может запросто выпасть с первой попытки. Именно так думал Брэди Харан, когда попросил сотни подписчиков своего сайта попробовать выбросить ятзи и записать бросок на видео. Как вы могли догадаться, некоторые выбросили ятзи после нескольких первых попыток, а многим это удалось после нескольких сотен бросков{45}.

В XVIII в., чтобы найти вероятность события, вы бы просто посчитали отдельные случаи: вы взяли бы отношение числа желаемых исходов к числу всех возможных случаев. «Честные» кости могут выпасть одной из возможных сторон, поэтому вероятность p того, что кость выпадает конкретной стороной, – 1/6. Но Бернулли задал вопрос иначе. Он хотел его расширить, чтобы включить проблемы, касающиеся болезней и погоды, с надеждой охватить другие научные вопросы{46}.