Глава 7 Треугольник Паскаля

В физическом мире не существует совершенной симметрии, искусственных машин с бесконечно малым допуском или идеальных моделей. Это мир множества скрытых переменных, явления которого слишком трудно охватить точной мерой. Иными словами, подлинные случайности действительно происходят, и мы часто обращаемся к вероятностным картинам событий, чтобы понять сложный феномен случайности.

Что если бы у вас обнаружили миелодиспластический синдром – редкую форму рака, при котором костный мозг не вырабатывает достаточно красных кровяных телец? Вы столкнулись бы с дилеммой: согласиться на трансплантацию костного мозга с 70 % вероятностью успеха или не делать ничего и с 70 % вероятностью умереть в течение следующих 10 лет. Конечно, у трансплантации имеются свои риски. Помимо необходимости химиотерапии и риска инфекции будет еще 30 % вероятность смерти в течение следующих 6 месяцев.

Брайан Зикмунд-Фишер, который преподает теорию рисков и теорию вероятностей в Медицинской школе Мичиганского университета, столкнулся с такой дилеммой в 1998 г. Ему диагностировали миелодиспластический синдром и сказали, что без лечения он проживет всего 10 лет, а с лечением у него будет 70 %-ная вероятность жить нормальной жизнью{63}. Он сделал ставку на трансплантацию. Смысл в том, что шансы ничего не говорят об отдельном человеке. Вероятность в 70 % получена посредством сбора статистических данных о сотнях (возможно, тысячах) людей, которые столкнулись с той же дилеммой, – государственная, нелокальная статистика. Статистические группировки описывают тенденции и возможности, а не отдельные случаи, когда можно выиграть или проиграть.

Возьмем некое событие, которое вы могли бы счесть редким. Его математические шансы могут быть один к миллиону, но, вероятно, такие цифры связаны с тем, что событие оценивается как локальный феномен. В качестве примера можно взять белку, которую ударило молнией в тот момент, когда она пересекала дорогу. Когда мы говорим на этом знакомом языке шансов, то часто выражаемся фигурально, без какого-либо последовательного метода определения терминов. Итак, «один на миллион» обычно применяется к событию, которое, как мы думаем, происходит в довольно широких пределах Соединенных Штатов. Но США – большая страна. Это нетрудно увидеть, пролетев над маленькими домиками, маленькими деревьями и обширными зелеными полями. Мы не думаем ни о том, сколько там внизу белок, ни о том, сколько из них пересекают дорогу в отдельный момент времени. Ученые оценивают численность белок в США в 1,12 млрд, что в 3 раза больше населения страны. И белки постоянно пересекают дороги.

Учитывая 1,12 млрд белок, 6,5 млн км дорог и 9,5 млн км² площади США, вполне возможно, что каждую минуту 300 белок пересекают дороги{64}. Во время грозы это число может быть даже больше. В среднем в Соединенных Штатах случается 110 000 гроз в год. Летом гроз гораздо больше, чем зимой, что делает возможность поражения белки ударом молнии летом действительно очень большой.

Каждое явление в природе вызывается большим числом неопределенных возможностей. Когда бросают игральную кость, то результат сильно зависит от ее начального положения в руке бросающего и значительно слабее – от звуковых волн, создаваемых голосами присутствующих в комнате. Это лишь два внешних фактора, направляющих кость к положению, в котором она остановится.

То, как она ударяется об стол, точность ее балансировки, ее движение по руке, упругость соударения со столом – все это повлияет на то, какая из сторон будет направлена вверх, когда кость остановится.

Рассмотрим игру, в которой возможен только выигрыш или проигрыш, а вничью сыграть невозможно. Пусть X обозначает исход испытания, а P (X) – вероятность наступления этого исхода. Если бы вы, например, бросали монету, P (орел) равнялось бы 1/2, как и P (решка). В колесе для американской рулетки 38 ячеек, включая 0 и 00: 18 красных; 18 черных; 0 и 00 – зеленые. Если вы ставите на красное, P (красное) равняется 18/38 или, если упростить, 9/19, а P (не красное) равняется 10/19. Если бы вы бросали игральную кость, надеясь выбросить «очко» (1), то P (1) равняется 1/6.

Выберите любую подобную игру и спросите себя: какова вероятность выиграть 0, 1, 2, 3 или 4 раза? Вполне уместный вопрос, поскольку реальные азартные игры предполагают совокупные последовательности выигрышей или проигрышей. Вспомним о Джоан Гинтер, о том, как она 4 раза выиграла в лотерею. Вам также могут быть интересны шансы сыграть лучше, чем если бы вы остались при своих, или по крайней мере шансы не проиграть больше 2 из 4 ставок.

Обозначим последовательностями из букв W и L серии выигрышей или проигрышей. Четырехкратный проигрыш будет обозначен через LLLL, а четырехкратный выигрыш – через WWWW. Есть лишь один способ выиграть все 4 раза и только один – не выиграть ни разу. А если выиграть 1 раз из 4? Есть 4 способа выиграть 1 раз из 4, а именно: WLLL, LWLL, LLWL и LLLW. И, конечно, способов проиграть только 1 раз из 4 также 4. Как насчет 2 выигрышей за 4 тура? Двухкратный выигрыш будет представлен 6 вариантами: WWLL, WLWL, WLLW, LWWL, LWLW и LLWW. При независимых событиях, где исход первого события не имеет памяти о других (например, туры при игре в рулетку или игра в орлянку), вероятности одного или другого из 2 событий – это произведение вероятностей каждого из них. Исходя из того, о чем мы говорили в главе 4, если A и B – это возможные исходы, вероятность наступления и A, и B – это произведение P (A) P (B), а вероятность наступления A или B – P (A) + P (B) – P (A) ? P (B).

Теперь давайте возьмем случай с 2 выигрышами. Чтобы упростить запись, примем, что p означает P (W), а q – P (L). Вероятность 1 отдельного выигрыша – p, и, поскольку выигрыш и проигрыш в разных турах – события независимые (т. е. каждый тур не зависит от предыдущего), мы видим, что вероятность 2 выигрышей в 4 турах – это p?q?[10]. Так происходит потому, что вам необходимо 2 раза выиграть и 2 раза проиграть, а когда логической связкой является «и», вероятности перемножают. Но, как мы выяснили, это может произойти 6 различными способами: WWLL, WLWL, WLLW, LWWL, LWLW и LLWW.

Поскольку логической связкой является «или», вероятность наступления любого из этих событий будет: ppqq + pqpq + pqqp + qppq + qpqp + qqpp, или просто 6p?q?.

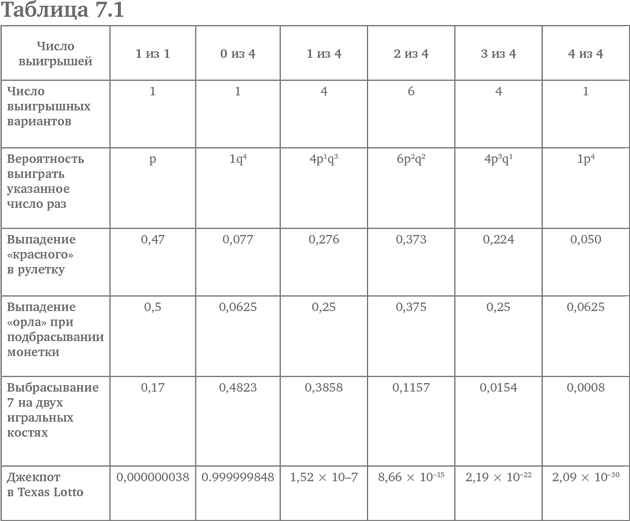
Рассмотрим четыре разные игры. В первой игре мы играем в рулетку и ставим на красное. Во второй мы подбрасываем монетку и ставим на выпадение орла. В третьей мы подбрасываем две игральные кости и выигрываем, если в сумме выпало 7, а во всех остальных случаях проигрываем. Наконец, в последней игре мы покупаем билет Texas Lotto и рассматриваем как выигрыш только джекпот. В таблице 7.1 приведены вероятности выиграть в каждой из этих игр (первый столбец). Мы также можем сыграть несколько раз. Допустим, мы играем четыре раза – тогда можем выиграть ноль, один, два, три или четыре раза. Вероятности соответствующих событий также приведены в таблице 7.1.

В теории и для рулетки, и для орлянки в соответствии с табл. 7.1 наиболее вероятен выигрыш в 2 турах из 4. Мы могли бы составить таблицу вероятностей для 100 туров рулетки и орлянки, однако это было бы ужасно долгим и непрактичным занятием. Вместо этого позвольте сказать только то, что в 100 турах орлянки игрок, ставящий на орла, с наибольшей вероятностью выиграет 50 раз, а в 100 турах рулетки, делая ставку на «красное», игрок с наибольшей вероятностью выиграет (как будет показано) только 37 раз{65}. Священный Грааль игрока – знать, какие именно 37 раз.

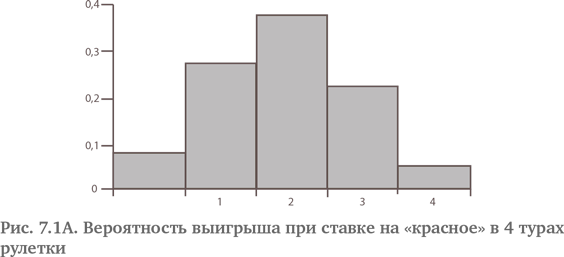
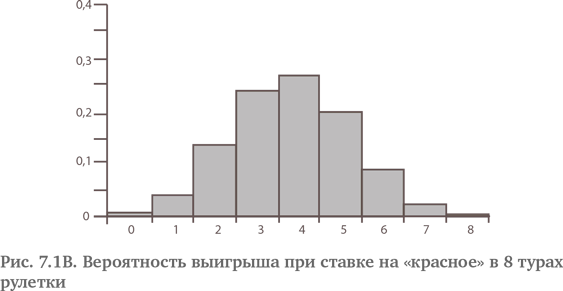
Отметим симметричность, присущую рулетке и орлянке, асимметричность костей и предельную асимметричность лотерей. Как насчет строки для рулетки в табл. 7.1? На гистограмме, изображающей число туров, когда выпадает «красное», против вероятности наступления этого количества туров, где выигрывает «красное» (см. рис. 7.1A), около числа 2 есть некоторая асимметрия, а центр притяжения (геометрическая точка равновесия), видимо, немного меньше 2. Когда число туров увеличивается до 8, отклонение становится еще более явным (см. рис. 7.1B){66}.

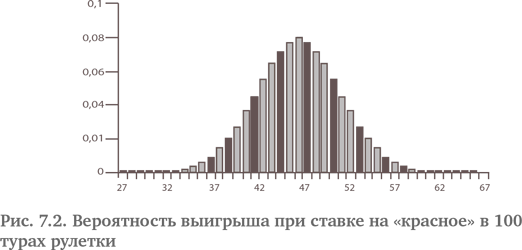
Увеличение числа туров в рулетке приводит к сглаживанию графика. Для 100 туров у нас будет 101 прямоугольник с основанием в одно деление{67}.

На рис. 7.2 изображено то, что называется частотным распределением. Высота прямоугольника над каждым из чисел означает то, как часто ожидается наступление отдельных событий. Столбцы распределяются по горизонтальной оси таким образом, что общая сумма их площадей равняется 1. Другими словами, площадь графика составляет 100 % всех возможных событий. Большая часть распределения частот концентрируется между 32 и 62, самый высокий столбец – 47. Меньше 32 и больше 62 вероятности настолько малы, что на графике их не видно. Например, P (31) = 0,00034, а P (63) = 0,0006. Весьма маловероятно, что «красное» выпадет 20 или 80 раз, однако, как все совпадения, не исключено.

В случае орлянки, где p равняется q, симметрия идеальна. Но p не обязательно равняется q. Мы обнаруживаем все более выраженную асимметрию по мере того, как увеличивается разрыв между p и q. В табл. 7.1 мы видим идеальную симметрию в 5-й колонке слева и почти никакой симметрии в 7-й колонке. И все же все вычисления основываются на 3-й колонке и производятся с помощью так называемого треугольника Паскаля – ключе к хранилищу инструментов теории вероятностей.

Треугольник Паскаля – это числа, расположенные в виде треугольника следующим образом:

Каждое число на рис. 7.3 – это сумма двух чисел, расположенных точно над ним в линии сверху: например, 3-е число (10) в 5-й линии сверху – это сумма 4 и 6 на 4-й линии. Сперва отметим симметричность, а затем обратим внимание на то, что числа те же, что мы видели, когда раскладывали по степеням сумму двух переменных p и q. Мы находим те же числа, когда раскладывали по степеням (p + q) n. Например, при n = 2 (p + q)? = (p + q) (p + q) = p (p + q) + q (p + q) = p? + pq + qp + q? = p? + 2p?q? + q?.

Если мы возведем в степень n = 1, 2, 3, 4, 5, 6…, получим следующую матрицу в форме треугольника:

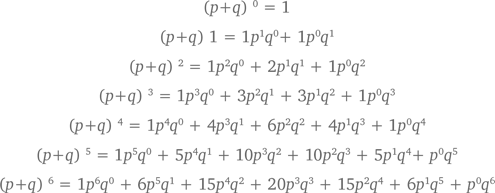
Для любого n константы в разложении двучленов (p + q)ⁿ – это как раз числа из треугольника Паскаля.

История этого треугольника начинается задолго до Блеза Паскаля{68}. Он в 1527 г. появился в работах китайского алгебраиста XIII в. Чу Шикей, позже – на титульном листе «Учебника по арифметике» Петера Апиана (который можно увидеть на картине «Послы» [1533 г.] работы Ганса Гольбейна-младшего), больше чем за век до того, как Паскаль исследовал треугольник, названный его именем{69}. В современном Иране треугольник известен как треугольник Хайяма, в честь известного персидского поэта и математика Омара Хайяма, который использовал треугольник в XII в., чтобы создать метод нахождения корней n-х степеней. В современном Китае он называется треугольником Ян Хуэя, в честь другого математика, который описал его в XIII в. В Италии это треугольник Тарталья, в честь математика Никколо Тарталья, жившего за век до Паскаля. Однако Паскаль, собрав уже известные наработки о треугольнике, использовал их в теории вероятностей{70}.