Хватит алгебры

Заглянув в школьные учебники, вы увидите множество всяких x, y и задач, которые сводятся к перестановкам чего-либо с привлечением толики здравого смысла. Есть масса толстенных книг по алгебре, поэтому понятно, что я не могу рассказать здесь обо всем, но вот еще одна задачка, которую алгебра помогает решить весьма точно и элегантно.

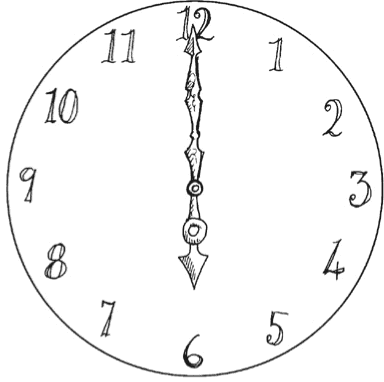
На старинных часах ровно 6 часов вечера. Сколько будет времени, когда минутная стрелка догонит часовую?

Разумеется, сложность в том, что часовая стрелка постоянно медленно движется. Как же это учесть?

Допустим, m – это количество минут, прошедших после 6 часов до того момента, когда минутная и часовая стрелки совпадут.

Минутной стрелке понадобится 30 минут, чтобы добраться до цифры 6, плюс пройти дистанцию, которую преодолеет часовая стрелка за m минут. Давайте это запишем:

Нам нужно выяснить, как далеко продвинется часовая стрелка за m минут.

Минутная стрелка делает один полный оборот в час. Часовой стрелке нужно 12 часов, чтобы сделать полный оборот, то есть ее скорость – 1/12 от скорости минутной.

Составим уравнение:

m = 30 + m/12

Число 12 в качестве знаменателя выглядит отвратительно, однако не волнуйтесь – мы умножим на 12 обе части уравнения:

12m = 360 + m

Перенесем + m в другую часть уравнения, поменяв знак:

12m ? m = 360

Вычтем 1m из 12m:

11m = 360

Разделим обе части на 11:

m = 32,727

Выходит, стрелки совпадут через 32,727 минуты после 6 часов вечера. Однако 0,727 минуты в ответе смотрятся некрасиво. Поскольку в минуте 60 секунд, в секундах это будет 0,727 ? 60, то есть около 44 секунд. Теперь у нас есть понятный ответ: стрелки совпадут в 6:32:44 вечера.