Разгадка тайн математики с помощью алгебры

Алгебра бывает крайне полезна при решении задач и головоломок. Вот вам кое-что для начала.

Земельная афера

Бэтчап Билдингз решил приобрести надел земли у фермера Шарпа. Обе стороны сошлись на том, что это должен быть квадратный участок 20 м ? 20 м, то есть площадью 400 квадратных метров, или м?. Однако приехав осмотреть землю, Бэтчап увидел, что участок имеет прямоугольную, а не квадратную форму!

Честно ли поступает фермер?

Хотя мы не знаем, на сколько метров стороны участка длиннее или короче, нам известно, что это одна и та же величина, давайте назовем ее x. Нарисуем схему участка.

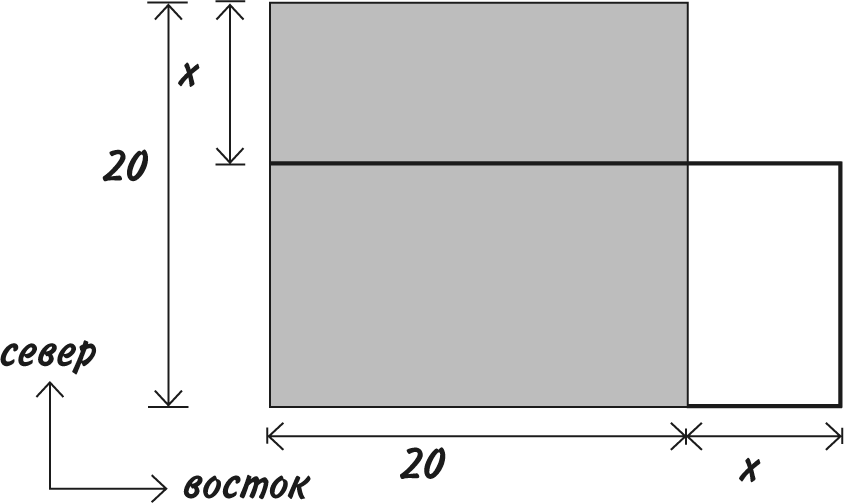
Серым цветом показано, как бы выглядел участок, будь это квадрат 20 м ? 20 м. Размеры же прямоугольника: (20 ? x) в северном направлении и (20 + x) в восточном. Чтобы узнать его площадь, перемножим эти значения и получим (20 ? x) ? (20 + x); знак умножения обычно не пишется: (20 ? x)(20 + x).

При перемножении двух выражений в скобках все, что находится внутри одной пары скобок, умножается на все, что находится внутри другой пары.

Для этого раскрываем первые скобки и умножаем каждый элемент в них на вторые скобки. Получаем:

(20 ? x)(20 + x) = 20(20 + x) ? x(20 + x) =

= 400 + 20x ? 20x ? x? =

= 400 ? x?

Как видите, раскрывая ?x(20 + x), мы первым делом умножаем ?x ? 20 = ?20x. Обратите внимание, знак «минус» никуда не исчезает. И наконец, умножаем ?x ? x, что дает ?x?. В следующей строке +20x и ?20x взаимоуничтожаются, и мы получаем любопытный результат: 400 ? x?. О чем это говорит?

Будь участок квадратным, Бэтчап приобрел бы обещанные 400 квадратных метров земли. Однако после изменения формы участка его площадь уменьшилась на x?. И чем больше значение x, тем больше земли теряет Бэтчап. (Помните, буква x обозначает, насколько стороны длиннее/короче одна другой.)

Если участок на 5 метров длиннее в одном направлении и на 5 метров короче в другом, тогда x = 5. Мы можем вычислить площадь такого участка двумя способами. Во-первых, взяв полученный ранее ответ 400 ? x? и подставив вместо x число 5. Площадь составит 400 ? 52, то есть 400 ? 25 = 375. Во-вторых, просто перемножив длины сторон прямоугольника. В северном направлении это 20 ? 5 = 15, а в восточном – 20 + 5 = 25. Тогда площадь равна 15 ? 25 = 375. Оба ответа совпадают, стало быть, алгебра работает как надо!

Разность квадратов

Допустим, у вас есть квадратный блок почтовых марок размером 6 ? 6. Кто-то оторвал от него несколько марок, оставив вам квадрат 4 ? 4. Сколько марок забрали?

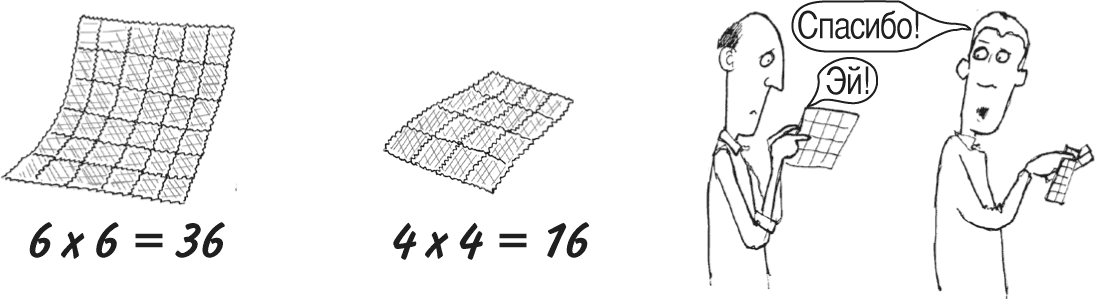
Нам нужно вычислить 62 ? 42. Вычитание квадрата одного числа из квадрата другого называется разностью квадратов. В данном случае все просто, поскольку числа небольшие. Получаем 36 ? 16 = 20. Однако есть более быстрый способ подсчета, который подходит для квадратов любых чисел.

Разность квадратов двух чисел равняется сумме этих чисел, умноженной на их разность.

Звучит довольно странно, однако вот что это означает: чтобы вычислить 62 ? 42, сначала нужно узнать сумму двух чисел: 6 + 4 = 10. Кроме того, понадобится их разность: 6 ? 4 = 2. Теперь умножаем сумму на разность: 10 ? 2 = 20. Такой же ответ мы получили раньше.

Вместо того чтобы рассуждать об этом на словах, проще записать правило разности квадратов в виде алгебраического уравнения. Обозначим буквой a первое число и буквой b второе, тогда наше правило будет иметь следующий вид:

a? – b? = (a + b)(a – b)

Мы уже наблюдали, как это работает для a = 6 и b = 4, однако данное уравнение подходит для любых a и b. Если вы думаете, что разность квадратов вам никогда не пригодится в жизни, представьте, что a = 20 и b = x, и посмотрите на уравнения из задачки о земельной афере. Там у нас (20 ? x)(20 + x) = 400 ? x?, тот же самый результат!

Объяснение загадки с тремя числами

Помните подраздел «Фокус с тремя числами», размещенный в начале книги? Там я объяснял, что какими бы ни были три последовательно идущих числа, если умножить большее из них на меньшее, результат всегда будет на единицу меньше второго числа, возведенного в квадрат. Например, возьмем 12, 13 и 14. Результат умножения 12 ? 14 = 168, что на единицу меньше, чем 132 = 169.

Опять воспользуемся уравнением для разности квадратов, подставив вместо b единицу. Вот что получится:

a? ? 12 = (a + 1)(a – 1)

Вспоминаем, что 12 = 1 ? 1 = 1, поэтому выходит

a? ? 1 = (a + 1)(a – 1)

Теперь предположим, что a – второе из трех последовательно идущих чисел. Тогда (a + 1) будет наибольшим числом, а (a ? 1) – наименьшим. Уравнение говорит нам, что если взять квадрат второго числа и вычесть из него единицу, то результат будет равен наибольшему числу, умноженному на наименьшее.

В случае с числами 12, 13 и 14 a = 13, но, разумеется, вместо 13 можно выбрать любое другое значение. Вот почему этот фокус применим к любым трем последовательно идущим числам.

Алгебра отлично подходит для разоблачения фокусов из серии «загадать любое число».

Как разрушить Вселенную

Помните, выше я предупреждал вас о такой вероятности? Если вы дочитали до этого места, значит, усердно трудились и многое узнали, поэтому будет совершенно справедливо вознаградить вас за старания неограниченными космическими суперспособностями…

Начнем с двух чисел, a и b, которые волей случая оказались равны:

a = b

Будем обращаться с обеими частями этого уравнения совершенно одинаковым образом. Смотрите внимательно…

Умножаем обе части на a: a? = ab

Вычитаем из обеих частей b?: a? – b? = ab – b?

С левой стороны уравнения получается разность квадратов, поэтому, как мы знаем, a? ? b? = (a + b)(a – b). С правой стороны выходит ab ? b?, где оба элемента делятся на b, стало быть, это выражение можно записать как b(a ? b). Все эти действия допустимы и абсолютно корректны.

Таким образом, получаем (a + b)(a – b) = b(a – b)

Теперь разделим обе части на (a – b) и получим (a + b) = b

Перед скобками множителя нет, а значит, их можно просто убрать

a + b = b

Переносим +b в другую часть уравнения, меняя знак:

a = b – b

И вот итог: a = 0

Теперь вспоминаем, что a и b могут быть любыми числами, следовательно, мы только что доказали, что любое число равно нулю. То есть получается, что любые измерения времени, пространства или веса несущественны: прощай, Вселенная!

Наша ошибка состояла в том, что мы разделили обе части уравнения на (a ? b). Но в случае, когда a = b, (a ? b) = 0. Единственное, чего нельзя делать одновременно с обеими частями уравнения, – это делить на ноль! Если, конечно, вы не собираетесь потратить денек-другой на попытки разрушить Вселенную…