Сфера

Около 2250 лет тому назад греческий ученый и математик Архимед совершил множество потрясающих открытий. Но лишь одно изображено на его могильной плите: Архимед был первым, кто доказал, что сфера, вписанная в цилиндр, занимает ровно 2/3 его объема. Иначе говоря, если взять банку с бобами в точности такого размера, чтобы в нее входил теннисный мяч, этот мяч вытолкнет наружу ровно 2/3 бобов. Благодаря Архимеду у нас теперь есть формула объема сферы.

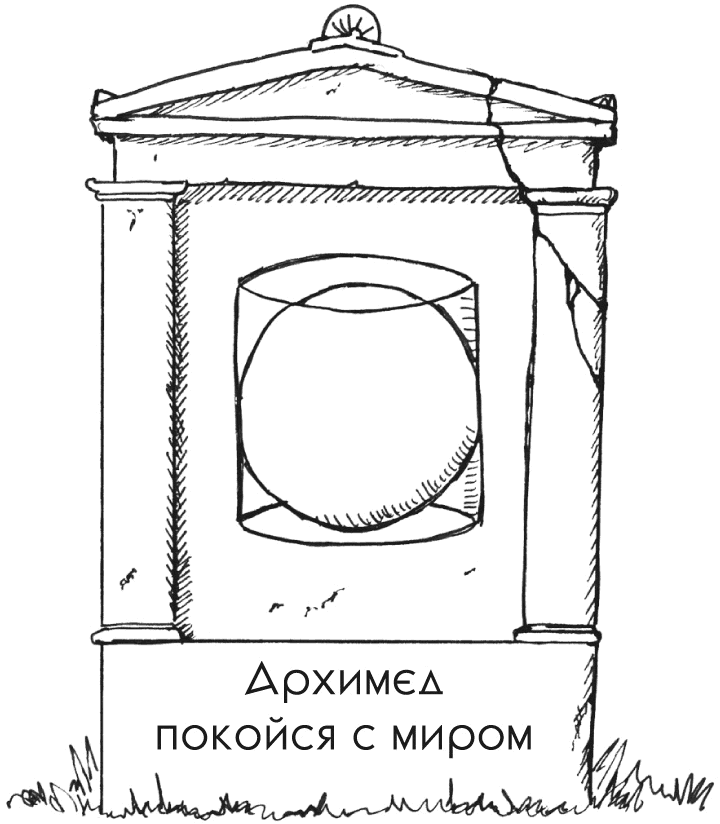
Итак, возьмем сферу и обозначим ее радиус r.

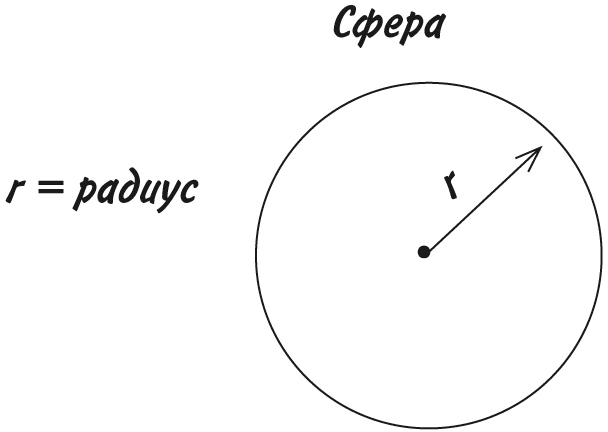
Сначала выведем формулу объема наименьшего цилиндра, в который помещается эта сфера. Возьмем обычную формулу объема цилиндра ?r?h, однако учитывая, что высота цилиндра в нашем случае равна 2r, объем наименьшего цилиндра будет ?r? ? 2r = 2?r?.

Согласно Архимеду, сфера занимает 2/3 этого объема, следовательно, объем сферы = 2/3 ? 2?r?. В итоге получается:

объем сферы = 4/3 ?r?

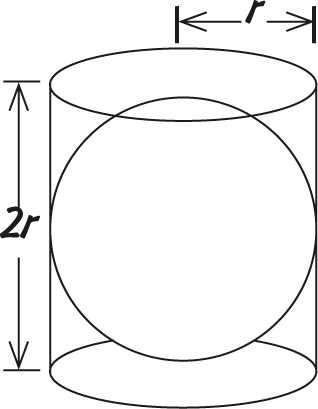
Раз уж мы занялись сферой, стоит упомянуть, что если разрезать ее пополам, площадь круга на срезе будет равна ?r?. А площадь поверхности сферы вчетверо больше площади круга, поэтому

площадь поверхности сферы = 4?r?

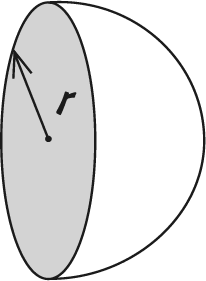
Формула объема сферы – еще одна весьма популярная на уроках геометрии тема, совершенно бесполезная в обыденной жизни: скажите на милость, как измерить радиус чего-то вроде футбольного мяча относительно его центра? Гораздо проще измерить его окружность с и воспользоваться такой формулой:

объем сферы = с?/60

Если вы ученый-ракетостроитель и вам нужен более точный результат, то вычисляйте так:

объем сферы = с?/59,2176264

Однако если вы ракетостроитель и учите математику по этой книге, то у нас у всех серьезные проблемы, не так ли?