Пифагор и его теорема

Пифагор жил примерно за 300 лет до Архимеда и прославился в первую очередь своей знаменитой теоремой: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов его катетов.

Звучит несколько замысловато, но взгляните на рисунок, и вы все поймете. Если взять прямоугольный треугольник и пририсовать к каждой его стороне квадрат, то площади двух меньших квадратов в сумме будут равны площади большого квадрата.

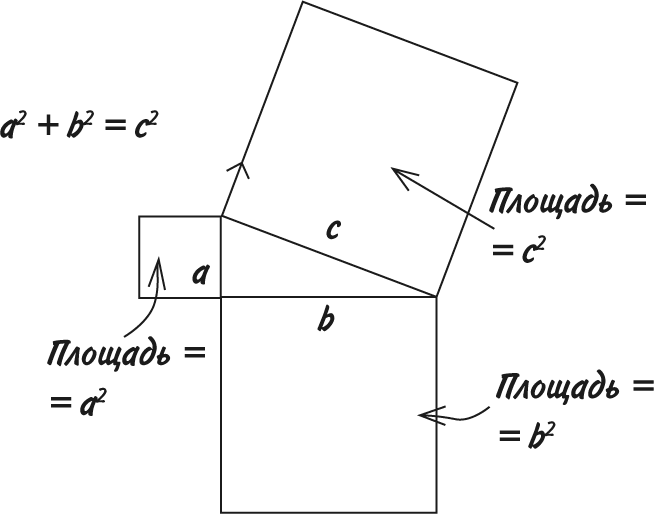
Если вас беспокоит вопрос, зачем кому-то понадобилось лепить к сторонам треугольника квадраты, не волнуйтесь, польза теоремы не в этом. Лучше представьте, что вы по диагонали пересекаете футбольное поле. Если размер поля 100 м ? 70 м, какое расстояние вам нужно преодолеть?

Вычисления будут не совсем простыми, поэтому, получив ответ, стоит убедиться, что он правдоподобен! По рисунку видно, что результат должен быть больше 100 м, но меньше 170 м.

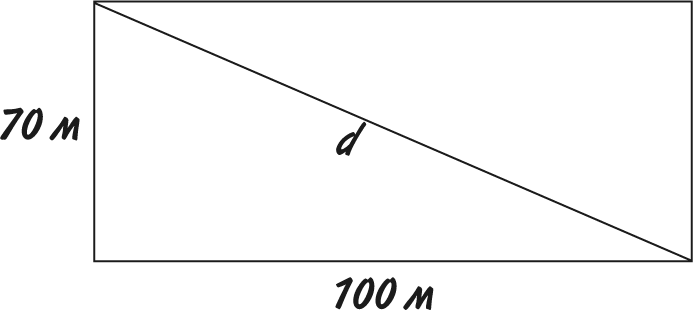
Обозначим диагональ буквой d.

Согласно теореме Пифагора, d? = 100? + 70?

Вычисляем: d? = 10 000 + 4900 = 14 900

Теперь нужно извлечь квадратный корень из 14 900. Иными словами, при умножении какого числа на само себя получится 14 900?

Если у вас нет калькулятора, самый простой способ извлечения корней – догадка и корректировка. Положим, вам кажется, что ответ может равняться 120, тогда считаем: 120 ? 120 = 14 400. Довольно близко, но все же меньше, чем надо. Ладно, попробуем 123 ? 123 = 15 129. Выходит больше, чем 14 900. Проверим еще один вариант 122 ? 122 = 14 884. Уже совсем рядышком, однако теперь все же посчитаем на калькуляторе.

Введите ‹14900 ?› и получите 122,065.

Значит, искомое расстояние чуть больше 122 м.

За более чем 2500 лет, прошедших со времени доказательства Пифагором этой теоремы, люди придумали не менее 300 других ее доказательств, основанных на сложных алгебраических вычислениях, чертежах и тригонометрии, а также следующий способ, где достаточно лишь посмотреть на несколько фигур:

Докажем, что a? + b? = c?

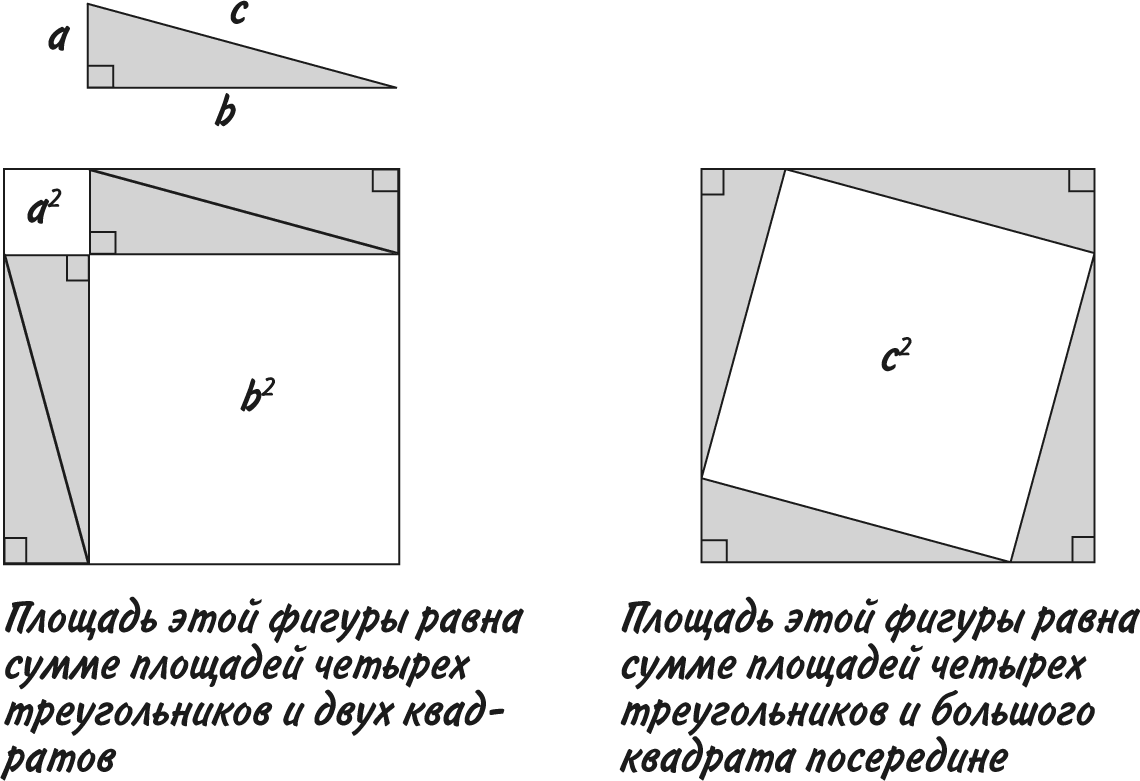
Внешние контуры обеих нижних фигур – это квадраты с длиной сторон (a + b). Это означает, что их площади равны и, следовательно, если из квадратов со стороной (a + b) вычесть площади четырех равных треугольников, то сумма площадей двух меньших квадратов будет равна площади большого квадрата. Вот мы и доказали, что a? + b? = c?!