Вечная молодость

В пределах Тихонии находится даже и проблема вечной молодости. На эту тему могут высказаться не только алхимики и розенкрейцеры, Питер Пэн, Дориан Грей и Хуан Понсе де Леон; знают ее и математики, и они говорят о ней на языке Тихонии. Они не пытаются остаться вечно молодыми и не спешат бежать в ногу с миром; не слишком интересует их и бессмертие. Вместо этого они заостряют внимание на более абстрактном, но и более практическом смысле этого термина, к которому можно применить средства математического анализа.

Если постановить категорически, что человек молод до тех пор, пока не достигнет определенного возраста, скажем тридцати или сорока лет, то дальше разговаривать, в сущности, не о чем. Никто не может оставаться молодым вечно. Но хронологический возраст — лишь одна из характеристик молодости и даже, возможно, не самая важная из них. Молодым также можно считать человека с долгим ожидаемым сроком жизни, и такое определение дает совершенно иную перспективу. Интуитивно не очевидно, но тем не менее справедливо, что ребенок в возрасте одного года «моложе», чем в момент рождения. Вероятность того, что новорожденный доживет, скажем, до шестидесяти, меньше, чем вероятность того, что годовалый ребенок проживет еще шестьдесят лет. В этом смысле годовалый младенец моложе. И чем дольше живет человек, тем короче становится оставшийся срок его жизни. А может быть, и нет.

Математики формулируют этот вопрос своим абстрактным образом: существует ли математический объект, не обладающий бессмертием, то есть в какой-то момент умирающий со стопроцентной вероятностью, но такой, что ожидаемая продолжительность его жизни не зависит от того, сколько он уже прожил?[52] Этот вопрос подразумевает, что даже вечно молодой организм рано или поздно умрет. В какой-то момент что-то внутри его ломается, и он умирает, но вероятность такого события не зависит от длительности жизни, прожитой организмом до этого момента. Вероятность того, что наш вечно молодой организм проживет, скажем, еще десять лет, сегодня такова же, какой она будет через год (если это существо еще будет живо), через двадцать восемь лет или через любое другое число лет. Это, разумеется, неверно в приложении к человеку. Прямо сейчас, в шестьдесят шесть, у меня больше шансов прожить еще десять лет, чем будет в девяносто четыре, то есть через двадцать восемь лет (если я к тому времени еще буду жив).

Ответ на этот вопрос таков: такой математический объект существует, и для каждой вероятности р того, что вечно молодое существо проживет еще одну единицу времени, существует, по сути дела, одна такая функция. Математики называют это распределение вечной молодости экспоненциальным распределением. На илл. 11 представлен график этого распределения при p = 2/3.

Как показано на илл. 11, через одну единицу времени (пусть это будет один год) площадь под кривой от 1 до бесконечности по оси x (заштрихованный участок) становится равна 2/3, и это означает, что у двух третей популяции продолжительность жизни составляет более одного года, то есть эти люди остаются в живых по прошествии года. Таким образом, вероятность того, что человек проживет этот первый год, действительно равна двум третьим. Аналогичным образом можно вычислить, что по прошествии двух лет в живых остаются четыре девятых популяции, то есть две трети от двух третьих исходной популяции, выживших к концу первого года, прожили еще один год. И так далее. В конце каждого года мы обнаруживаем, что две трети популяции, сумевшей остаться в живых, прожили еще год. (Если численность исходной популяции была равна А, то через t лет численность выжившей популяции будет равна A · (2/3)^t.) Из-за того что переменная t стоит на месте показателя степени, эту функцию и называют экспоненциальной, то есть показательной. На самом деле математические соображения, которые привели к ее открытию, гораздо менее сложны, чем в случае распределения Гаусса, так что этот математический объект, несомненно, тоже относится к плодам математики Тихонии.

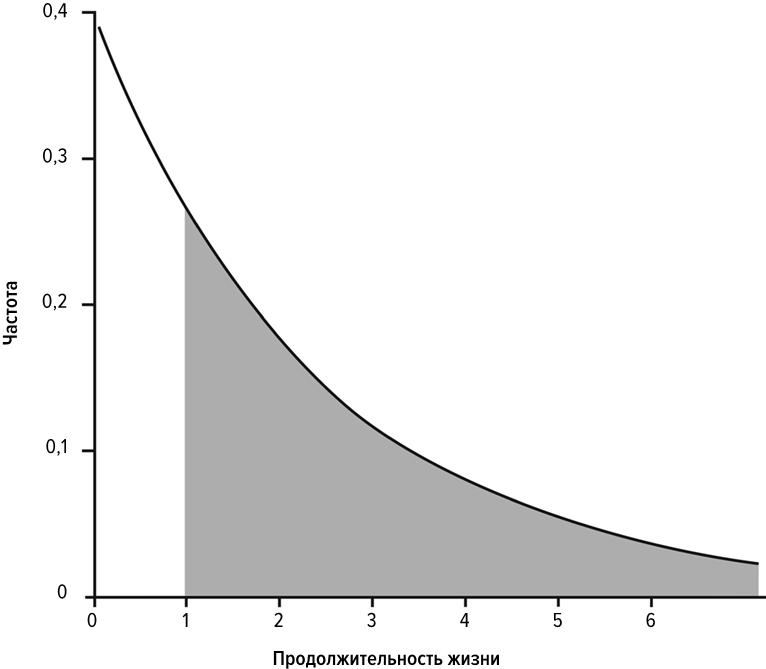
Илл. 11. Экспоненциальное распределение

(График Йожефа Бенце)

Таким образом, оказывается, что вечную молодость — по меньшей мере в математическом смысле — нельзя назвать теоретически невозможной. Но существуют ли такие объекты в реальном мире? Это уже вопрос не математический, а естественно-научный. Математика лишь говорит, что поиски таких источников вечной молодости не лишены смысла и она готова их моделировать, если только они будут найдены.

На самом деле существуют и природные, и искусственные объекты, к которым применимо это описание. Например, радиоактивная частица рано или поздно непременно должна распасться, но вероятность ее распада в течение следующих десяти минут в точности такая же, как вероятность ее распада через пять лет и десять минут, считая от настоящего момента, если ей удастся просуществовать эти пять лет. Другими словами, ожидаемое время до распада радиоактивной частицы совершенно независимо от времени ее существования. Такие частицы вечно молоды, и ожидаемая продолжительность их жизни соответствует экспоненциальному распределению.

То же описание весьма хорошо применимо и к некоторым бытовым предметам — например, к неоновой лампе. Рано или поздно (и обычно все-таки рано) любая неоновая лампа перегорает. Но ожидаемое время, остающееся до ее перегорания, не зависит от длительности ее горения. То есть теоретически уже бывшая в употреблении неоновая лампа ничем не хуже только что изготовленной. Она вечно остается молодой.

Экспоненциальное распределение полезно и для описания других явлений — например, длительности обычных телефонных разговоров. Длительность разговоров по-настоящему увлеченных сплетников распределена экспоненциально. Это означает, что, хотя даже сплетники рано или поздно вешают трубку, количество времени, в течение которого они готовы продолжать разговор, почти совершенно не зависит от того, как долго они уже проболтали. Сплетничество никогда не стареет.

Хотя вечная молодость не противоречит смертности — эти две черты прекрасно уживаются друг с другом, — в царстве биологии мы не находим вечно молодых. Организмы стареют и умирают. Почему же эволюция так и не породила нестареющего растения или животного?[53] Ответ на эту головоломку, насколько мы понимаем ее сейчас, весьма прост: стратегия выживания видов, которую выработала эволюция, использует генетическое разнообразие для обеспечения определенного уровня стабильности популяции особей перед лицом непредсказуемого воздействия среды. Другими словами, выгодно, чтобы соотношение долей разных характеристик в популяции оставалось более или менее постоянным из поколения в поколение. Если окружающая среда изменяется — но не слишком сильно, — вид обычно обладает достаточным разнообразием, чтобы некоторые особи заведомо смогли пережить такое изменение условий, даже если большинство представителей вида и погибнет. Затем выжившие размножатся и передадут своим потомкам новый набор характеристик, по всей вероятности лучше приспособленный к новым условиям. Такая стратегия требует вымирания старых генетических комбинаций (родителей) ради освобождения места для новых (детей), так что бессмертию в ней места нет.

Таким образом, разнообразие и стабильность — два важнейших фундаментальных принципа биологии — по-видимому, исключают вечную молодость. Возможно, не вечную жизнь, но определенно вечную молодость. Вечно молодое либо нестабильно, либо единообразно. Одна радиоактивная частица ничем не отличается от другой, и то же справедливо и в отношении неоновых ламп. Тот, кто вечно молод душою — то есть открыт всему в течение всей своей жизни, — платит за это дорогую цену: он никогда не приобретет ни мудрости, ни жизненного опыта.

Вечная молодость — явление с окраин Тихонии. Возможно, не так уж и важно, что она несовместима с жизнью и разнообразием. Напротив, захватывающие дух явления Диконии происходят из других источников.