Между Гауссом и Коши

В начале этой книги, когда мы впервые столкнулись с мирами Тихонии и Диконии, мы использовали распределение Гаусса для описания Тихонии и распределение Коши для описания Диконии. На илл. 5 мы сравнили графики этих двух распределений и увидели, что кривая Гаусса приближается к оси x гораздо быстрее, чем кривая Коши, что «хвост» распределения Коши гораздо толще, чем у распределения Гаусса, и что кривая Коши тоньше и острее в середине.

С вашего разрешения я еще раз воспроизведу здесь илл. 5, чтобы ваша книга не слишком растрепалась от постоянного перелистывания взад и вперед (илл. 21). Выше мы отмечали, что радикальное различие между Тихонией и Диконией есть следствие небольшого, как кажется, математического различия между двумя распределениями. Вам, возможно, приходил в голову следующий вопрос: если нам удалось создать настолько разные миры на основе двух просто описываемых математических кривых, то почему бы не построить третью кривую, лежащую где-то между первыми двумя, чтобы создать мир, свойства которого будут промежуточными между распределениями Гаусса и Коши? Если такая мысль действительно вас посещала, значит, вы хорошо чувствуете математическое мышление. На самом деле все распределения, описывающие связи между вершинами безмасштабных сетей, оказываются где-то между Гауссом и Коши. Если Тихония характеризуется распределением Гаусса, а Дикония — распределением Коши, то масштабно-инвариантные математические объекты находятся где-то в промежутке между этими двумя случаями.

Чем меньше фактор Мандельброта безмасштабной сети, тем более распределение связей между ее вершинами приближается к распределению Гаусса. Другими словами, малые значения фактора Мандельброта соответствуют более тихим сетям. Тем не менее безмасштабная сеть никогда не бывает настолько тихой, чтобы стать предсказуемой; она всегда остается хаотичной. Тихая безмасштабная сеть описывает сравнительно тихий хаос. Верно и обратное: чем больше фактор Мандельброта сети, тем ближе распределение связей между ее вершинами оказывается к распределению Коши. Это означает, что в более диких сетях узлы крупнее, чем в более тихих.

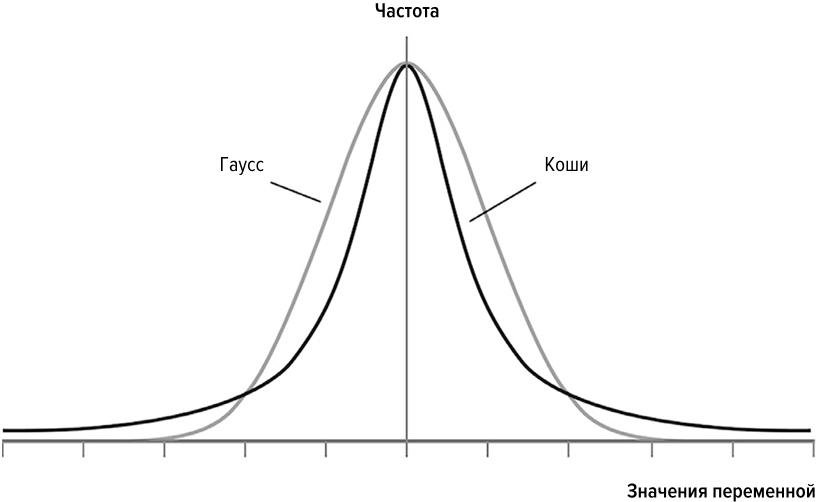
Илл. 21. Сравнение распределений Гаусса и Коши

(График Йожефа Бенце)

Переход между распределениями Гаусса и Коши становится особенно интересным, если попытаться выяснить, имеет ли промежуточное распределение стандартное отклонение. Из того, о чем мы говорили раньше, мы помним, что у распределения Гаусса есть стандартное отклонение, а у распределения Коши его нет. Математически доказано, что у масштабно-инвариантных распределений, фактор Мандельброта которых меньше 1, есть хорошо определенное стандартное отклонение, а те, фактор Мандельброта которых больше или равен 1, его не имеют[101]. Это показывает, что весь диапазон от тихого до дикого действительно занимают безмасштабные сети. Тем не менее всякая безмасштабная сеть хаотична.

В главе 7, которая называлась «Математика непредсказуемого», я дал очень узкое определение хаоса и отметил, что существуют объекты даже более хаотичные, чем те, которые удовлетворяют нашему определению хаоса. То же можно сказать и о безмасштабных сетях. Если, например, число соединений, исходящих из каждой вершины, определяет наша снайпер Фиби, то сеть уже не будет ни безмасштабной, ни хаотической в смысле нашего определения. Получится нечто гораздо более беспорядочное. Как мы увидим в дальнейшем, в реальном мире существуют сети, не относящиеся к безмасштабным и гораздо более хаотические, чем те, которые к этому разряду относятся.