Золотой век математических игр: XVII и XVIII века
Книга де Мезириака — своеобразный конспект по занимательной математике той эпохи. В ней описана задача о волке, козе и капусте, магические квадраты, задачи о целых числах и взвешиваниях, например: «Найти минимальное число гирь и их массу, с помощью которых на простых весах с двумя чашками можно измерить любой вес, выраженный целым числом от 1 до 40».
Начиная с этого момента, уже в XVII веке появляется множество книг похожего стиля. В 1624 году Анри ван Эттен (это псевдоним французского иезуита Жана Лёрешона) опубликовал книгу Recreations mathematiques («Развлекательная математика»), которая стала более успешной, чем книга Баше, и послужила образцом для последующих изданий, среди которых работа Клода Мидоржа, изданная во Франции в 1630 году и переведенная на английский уже в 1633 году, или работа Даниэля Швентера, опубликованная в 1636 году в Германии. Но самой известной в XVIII и XIX веках стала книга Жака Озанама Recreations mathematiques et physiques («Математические и физические развлечения»), которую в 1725 году отредактировал и дополнил математик и историк науки Жан Этьен Монтукля.
Среди трудов XVIII века упоминания заслуживает книга Rational Recreations Уильяма Хупера («Рациональные развлечения», 1774), где впервые упоминается одна из задач об исчезновении клетки — великолепный пример того, как для решения простой с виду задачи используются интересные математические свойства.

Портрет математика и лингвиста Даниэля Швентера.
Хотя мы перечислили некоторых авторов книг об играх и занимательной математике, не будем забывать, что многие великие математики XVII—XIX веков сформулировали и впоследствии решили задачи, ставшие классикой жанра. Наиболее выдающиеся среди них — Исаак Ньютон (1642—1727), Леонард Эйлер (1707— 1783) и Карл Фридрих Гаусс (1777—1855).
Ньютон в своей книге Arithmetica Universalis («Универсальная арифметика»), написанной на латыни в 1707 году, наряду с важными для математики проблемами упоминает и о простейших занимательных задачах. Хотя наиболее известна так называемая задача о коровах, ниже мы приведем другую задачу, где показывается связь вероятностей и азартных игр. Одновременно бросается некоторое число обычных игральных костей. Вероятность какого из следующих событий наибольшая?
1) При броске 6 кубиков выпадет хотя бы одна шестерка.
2) При броске 12 кубиков выпадут хотя бы две шестерки.
3) При броске 18 кубиков выпадут хотя бы три шестерки.
Читатель с легкостью сможет решить эту задачу после того, как ознакомится с аналогичными задачами, о которых рассказывается в главе 3.
Эйлер, перу которого, возможно, принадлежит наибольшее число работ среди всех математиков, также написал множество занимательных книг, например по комбинаторике, посвященных греко-латинским квадратам. Речь идет о разновидности магических квадратов, в которых необходимо расположить n символов в квадрате n ? n клеток так, чтобы в каждой строке и в каждом столбце находились все возможные символы. Можно сказать, что эти квадраты стали прообразом современных судоку. Но, вне всяких сомнений, самая известная из его задач — задача о кёнигсбергских мостах, которую Эйлер опубликовал на латыни в 1759 году в бюллетене Прусской академии наук. Эта задача дала начало теории графов. Граф — это графическое представление отношений между элементами множества, состоящее из вершин (элементов множества) и ребер, соединяющих вершины (связанные между собой элементы). Теория графов используется преимущественно для формулировки и решения задач оптимизации.
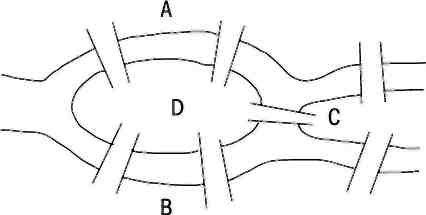
Задача о кёнигсбергских мостах звучит так: можно ли обойти все четыре части города, пройдя при этом по каждому из мостов ровно один раз? Эйлер показал, что такого пути не существует, и определил, при каких условиях подобные задачи имеют решение.
Наконец, Гаусс, внесший огромный вклад в математику, также уделял время занимательным задачам, среди которых задача о восьми ферзях: нужно расположить на шахматной доске восемь ферзей так, чтобы ни один из них не находился под боем другого. Также нужно найти количество разных решений и обобщить задачу для n ферзей и доски n ? n. Используя интуитивный метод, а затем систематизировав его и переформулировав задачу в терминах перестановок, Гаусс показал, что задача имеет 92 различных решения.

На этой доске размером 8x8 показано одно из решений задачи о восьми ферзях.
ПАРАДОКС ХУПЕРА
В этой головоломке дан квадрат со стороной 8 клеток, разделенный на два треугольника и две трапеции. Из этих же фигур составляется прямоугольник размерами 5x13 клеток. Получается, что площадь квадрата (64 клетки) равна площади прямоугольника (65 клеток), и это «доказывает», что 64 равно 65. Читатель обнаружит, что составить подобный прямоугольник невозможно, и увидит, где же скрывается «дырка» площадью в 1 клетку.
Даже если считать парадокс решенным, он не перестает представлять интерес с точки зрения математики. Если проанализировать задачу подробнее, становится ясно, что она далеко не так проста. Если расположить длины сторон фигур в порядке возрастания, получим 3,5,8,13 — числа Фибоначчи. Эта последовательность имеет такое свойство: квадрат произвольного члена последовательности равен произведению предыдущего члена на последующий плюс (или минус) 1. Иными словами, an2 =аn-1 · аn+1+(-1)n+1. Таким образом, взяв квадрат со стороной, равной одному из чисел Фибоначчи, и прямоугольник, стороны которого равны предыдущему и последующему числам Фибоначчи, мы снова получим такой же парадокс. Этот парадокс разрешим, и подобное построение можно выполнить корректно для числа Ф, описывающего золотое сечение, которое тесно связано с числами Фибоначчи: взяв квадрат со стороной Ф и разделив его на четыре части, получим прямоугольник со сторонами 1 и Ф + 1. Площадь квадрата (Ф2) будет точно равна площади прямоугольника 1 · (Ф + 1).
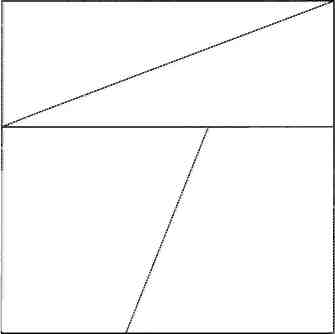
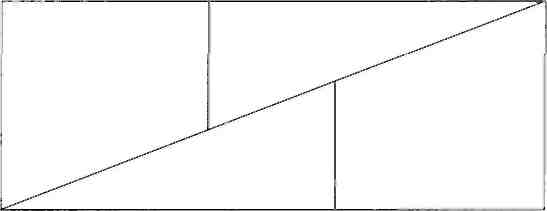
Парадокс Хупера гласит, что из двух треугольников и двух трапеций, образующих квадрат, можно составить прямоугольник большей площади.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК