Задача 2: играем в бридж

Игрок в бридж при раздаче получает 13 карт. Сколькими способами он может упорядочить карты?

Если у игрока 13 карт, то первую по порядку он может выбрать тринадцатью возможными способами, вторую — двенадцатью, третью — одиннадцатью и так далее до последней карты, которую можно будет выбрать единственным способом (она останется последней неупорядоченной). Следовательно, общее число возможных вариантов упорядочения карт равно:

13 • 12 • 11 • … • 3 • 2 • 1 = 13! = 6 227 020 800.

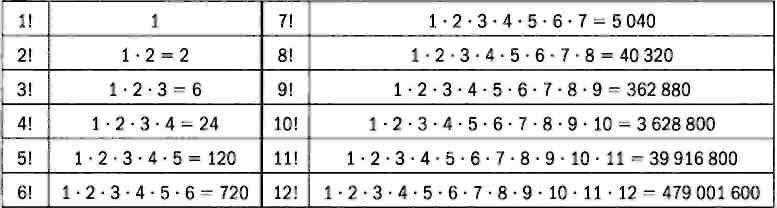
Эта операция называется перестановкой 13 элементов, и результат можно также записать в виде факториала. Факториал обозначается восклицательным знаком после числа. В нашем случае результат равен 13!. По определению n! равен произведению всех натуральных чисел от n до 1. В таблице ниже приведены значения факториала для первых 12 чисел, чтобы дать представление о том, насколько быстро он возрастает.

Подсчет лежит в основе множества карточных игр. Картина Лукаса ван Лейдена «Игроки в карты», 1520 год.