Математика сотрудничества: игры с ненулевой суммой

Чтобы показать разницу между играми с нулевой и с ненулевой суммой, рассмотрим ситуацию, связанную с распространением рекламы. Две компании, А и Б, хотят прорекламировать свою продукцию. В обе компании поступает предложение от телеканала: рекламу можно показать днем (когда ее увидят 40% телезрителей) или вечером (тогда ее увидят 60% зрителей), причем можно выбрать только один из предложенных вариантов. Известно, что дневная и вечерняя аудитории не пересекаются. Если обе компании закажут рекламу на одно и то же время, то их продукцию купят 30% зрителей, включивших телевизор в это время, и никто из тех, кто смотрел телевизор в другое время. Если же компании закажут рекламу на разное время, то охватят 50% аудитории, которая в тот момент находилась у экранов. Какое решение оптимально для каждой компании? Будет лучше проконсультироваться с другой компанией или скрыть свои намерения?

Эту игру можно выразить в виде платежной матрицы, значения которой будут соответствовать доле аудитории. Однако в этом случае в каждую ячейку таблицы нельзя поместить какое-то одно значение, так как выигрыш одной компании не равен проигрышу другой и каждая компания будет иметь свою выгоду. По этой причине элементами матрицы будут пары значений. Первое число в каждой паре — выгода компании А, второе — выгода компании Б в зависимости от стратегий, выбранных обеими компаниями.

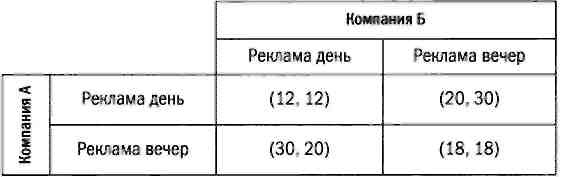
Если А и Б запустят рекламу днем, то каждой компании достанется 12% аудитории (30% от 40%). Если рекламные ролики выйдут в разное время, то результаты будут симметричны: если А запустит рекламу днем, а Б — вечером, то А получит 20% (половину от 40%), компания Б — 30% (половину от 60%). Если обе компании в этом случае сменят стратегии на прямо противоположные, противоположными окажутся и результаты.

Для анализа этой игры аналогично тому, как мы это делали ранее, нужно рассматривать две матрицы (с выигрышами каждого игрока), учитывая, что каждый игрок стремится максимально увеличить свой выигрыш в соответствии с платежной матрицей.

МАТРИЦА ДЛЯ ИГРОКА А

МАТРИЦА ДЛЯ ИГРОКА Б

С учетом того, что матрицы симметричны и что стратегии А указаны в строках, а стратегии Б — в столбцах, анализ обеих матриц проводится аналогичным образом. Можно выполнить те же действия, что и для игр с нулевой суммой: седловая точка отсутствует (максиминное значение равно 18, минимаксное — 12), поэтому нужно найти смешанную стратегию, чтобы определить цену игры для игрока А. Эта стратегия такова: нужно использовать стратегию 1 (выпускать рекламу днем) с вероятностью 3/5 и стратегию 2 (выпускать рекламу ночью) с вероятностью 2/5. Таким образом мы получим цену 19,2 (средний выигрыш за партию). Аналогично для игрока Б (с учетом симметрии): в каждых пяти партиях он должен произвольным образом два раза выбрать стратегию 1 и три раза — стратегию 2, при этом его средний выигрыш будет тем же. Пока что нет никаких отличий от прошлых примеров, и читатель может посчитать, что мы определили оптимальную стратегию для каждого игрока и что игра решена.

Однако более подробный анализ игры показывает, что в этом случае каждый из двух игроков ожидает выиграть больше, и при этом выигрыш другого игрока останется прежним. Поэтому предыдущее решение не является оптимальным, и цена игры, найденная для оптимальных смешанных стратегий, используемых в играх с нулевой суммой, не всегда является наибольшей.

Это происходит потому, что оптимальные стратегии в играх с нулевой суммой основаны на ограничении или уменьшении выигрыша соперника. Если игра имеет нулевую сумму, то уменьшение выигрыша одного игрока равносильно увеличению выигрыша другого, но в нашем случае это не так. Допустим, что компания Б не будет использовать смешанную стратегию и всегда будет применять стратегию 2 (выпуск рекламы вечером), в то время как компания Б будет придерживаться смешанной стратегии. В этом случае компания А в среднем получит 30 • 2/5 + 18 • 3/5 = 22,8, а компания Б — по-прежнему 19,2. Заметим, что выигрыш Б не изменился, а выигрыш А возрос. В играх с нулевой суммой это невозможно. Очевидно, компания Б может действовать подобным образом и всегда использовать чистую стратегию 2, ожидая, что А будет придерживаться смешанной стратегии. В этом случае результат Б возрастет, результат А останется на прежнем уровне.

Но что произойдет, если обе компании используют чистую стратегию 2? Обе получат лишь по 18% аудитории, выигрыш обоих игроков уменьшится одинаково. Кажется, что мы зашли в тупик: каждая компания может выиграть больше, не повредив конкуренту, но если оба игрока захотят получить больше, то, напротив, выиграют меньше среднего ожидаемого значения.

Однако возможен и другой вариант. Допустим, что оба игрока заключили соглашение, чтобы не попасть одновременно в клетки с наименьшим выигрышем, то есть не размещать рекламу в одно и то же время. В этом случае каждая компания получит больше, при этом выигрыши компаний могут стать равными: если компания А будет чередовать стратегии 1 и 2, а компания Б — чередовать стратегии 2 и 1, то средний выигрыш для обеих компаний будет равен 25% за партию. Компания А будет попеременно получать 20 и 30 процентов, компания Б — 30 и 20. Это решение кажется оптимальным и, более того, является равновесным.