Задача о ресторане

Двое друзей, Мария и Георгий, хотят открыть ресторан у перекрестка больших дорог за городом, который окружают горы. У них не возникло никаких разногласий, кроме одного: Мария хочет открыть ресторан в низине, а Георгий — высоко в горах, и в этом вопросе их мнения полностью противоположны. Чтобы принять решение, они придумали провести игру: друзья выбрали три параллельных автомагистрали Al, А2 и АЗ, которые идут с запада на восток, и три параллельных дороги С1, С2 и СЗ, которые идут с севера на юг. Эти дороги образуют девять перекрестков. Высота каждого перекрестка приведена в следующей матрице:

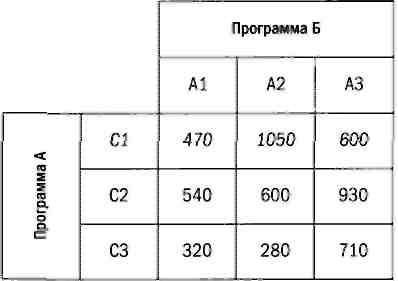
Чтобы определить место будущего ресторана, компаньоны решили действовать так: Мария выбирает одну автомагистраль (Al, А2 или АЗ), Георгий — другую (Cl, С2 или СЗ). На пересечении выбранных дорог и будет построен ресторан. Как должен действовать каждый игрок, чтобы ресторан в итоге был построен в соответствии с его интересами?

Георгий — пессимист и из трех минимальных значений (470, 540, 280) выбирает максимум. Он решает выбрать дорогу С2, что гарантирует высоту в 540 метров. Аналогично Мария оценивает максимальную высоту каждой дороги (540, 1050, 930) и выбирает трассу А1, что обеспечивает наименьшую высоту, 540 метров. Итак, оба игрока сделали свой выбор и результат в 540 метров является оптимальным для каждого из них. Иными словами, если один из компаньонов изменит свой выбор, то результат будет меньше соответствовать его интересам.

С одной стороны, эти примеры показывают разнообразие ситуаций, в которых можно найти решение, устраивающее обе стороны с противоположными интересами. С другой стороны, если матрица имеет седловую точку, то результат полностью определяется оптимальным выбором, совершенным обоими соперниками.