Образцовое решение

У нас, однако, есть более рациональный метод, а именно учет всех возможных значений d. Прежде всего, мы замечаем, что q должно быть целым числом, а значит необходимо выделить дробную часть q, т. е. 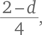или d = 2–4k. Подставив это в приведенное выше уравнение, мы получаем q = 10 + k, а n = 20 — q — d = 20 — (10 + k) — (2–4k), или n = 8 + 3k.

Поскольку d = 2–4k, значение k может быть либо нулевым, либо отрицательным.

В таблице ниже приведены возможные значения k и вытекающие из него значения d, q и n.

При k = 0, –1, –2 мы получаем реальные варианты. Когда же k = –3, d = 2–4(–3) = 14, а n = 8 + 3(–3) = –1, что не имеет смысла в этой задаче. Таким образом, количество сочетаний, при которых сумма составляет $3,10, равно трем.