ГЕРОНА ФОРМУЛА
Эта формула позволяет вычислить площадь S треугольника по его сторонам a,b и c:
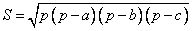 ,
,
где p - полупериметр треугольника, т.е. p = (a + b + c)/2. Формула названа в честь древнегреческого математика Герона Александрийского (около I в.). Герон рассматривал треугольники с целочисленными сторонами, площади которых также являются целыми числами. Такие треугольники называют героновыми. Например, это треугольники со сторонами 13, 14, 15 или 51, 52, 53.
Существуют аналоги формулы Герона для четырехугольников. В связи с тем что задача на построение четырехугольника по его сторонам a,b,c и d имеет не единственное решение, для вычисления в общем случае площади четырехугольника недостаточно только знания длин сторон. Приходится вводить дополнительные параметры или накладывать ограничения. Например, площадь вписанного четырехугольника находится по формуле:
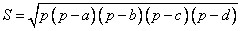 .
.
Если же четырехугольник и вписанный, и описанный одновременно, его площадь находится
по более простой формуле: 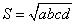 .
.
Более 800 000 книг и аудиокниг! 📚
Получи 2 месяца Литрес Подписки в подарок и наслаждайся неограниченным чтением
ПОЛУЧИТЬ ПОДАРОК