ФЕРМА МАЛАЯ ТЕОРЕМА

Знаете ли вы об удивительном свойстве, которым обладают числа, составленные из одних девяток? Каково бы ни было простое число p, отличное от 2 и 5, всегда можно указать такое число, составленное из одних девяток - 9999...99, - что оно будет делиться на p. Так, на 3 делится 9, на 7 - число 999999, на 11 - число 99, на 13 - опять-таки число 999999. Чтобы получить число, делящееся на 17, придется взять число из 16 девяток, на 19 - число из 18 девяток. И всегда можно быть уверенным, что нужное число найдется, хотя и может оказаться очень длинным.

На чем основано доказательство этого факта? Дело в том, что при делении с остатком на p может встретиться конечное число различных остатков: 0,1,2,...,p-1. Поэтому найдутся два числа из девяток (пусть одно - из l девяток, а другое - из m девяток, l > m), такие, что оба они при делении на p дают один и тот же остаток. Тогда число из l-m девяток будет делиться на p. Заметим, что обсуждаемое утверждение равносильно тому, что для всякого простого p, не равного 2 и 5, существует число вида 1000...00 (единица с нулями), дающее при делении на простое число p остаток 1. Это очень важное утверждение. На нем основана, например, периодичность бесконечной десятичной дроби, полученной при обращении обыкновенной дроби 1/p, где p ≠ 2 и p ≠ 5 (если выписывать последовательные десятичные знаки при делении 1 на p, то с некоторого места они начнут периодически повторяться).

Другая связь имеется с признаками делимости. Признак делимости на 3 основывается на том, что 9 делится на 3. Для того чтобы узнать, делится ли на 11 число 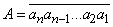, достаточно разбить его на двузначные числа справа налево:  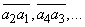(последнее число может оказаться однозначным), сложить эти числа, и если полученная сумма делится на 11, то на 11 делится и A, а если не делится, то и A не будет делиться. Этот признак делимости основывается на том, что 99 делится на 11. Аналогичный признак делимости с разбиением на трехзначные числа имеется для 37. Такие признаки делимости можно построить для всех простых чисел p, не равных 2 и 5, но они могут оказаться неудобными.

Естественно попытаться уточнить, сколько же в точности девяток надо взять, чтобы получилось число, делящееся на p. Оказывается, что всегда годится число, состоящее из p-1 девяток. Однако иногда достаточно и меньшего числа, но всегда это наименьшее число девяток l является делителем p-1. До сих пор не известен ответ на вопрос, волновавший еще Гаусса: конечно или бесконечно число таких p, для которых l=p-1 (так обстоит дело для p=7,17,19,23,47,...).

Утверждение о делимости чисел, составленных из девяток, является частным случаем значительно более общего утверждения, носящего название малой теоремы Ферма: если p - простое число, a - натуральное число, не делящееся на p, то a^p-1 при делении на p дает остаток 1 (утверждение о девятках получается при a=10). «Меня озарило ярким светом», - писал Ферма, впервые сообщая об этом своем открытии в письме (1640). В самом деле, эта теорема стала одним из самых фундаментальных фактов в теории делимости натуральных чисел. Ферма не оставил доказательства теоремы, и первое известное доказательство принадлежит Л. Эйлеру. В заключение дадим формулировку этой теоремы, не содержащую ограничений на число a: если p - простое число, a - натуральное число, то a^p - a делится на p.