ОПРЕДЕЛИТЕЛЬ

Определитель - число, поставленное по определенным правилам в соответствие квадратной матрице.

Определителем квадратной матрицы второго порядка 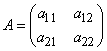 называют число a₁₁a₂₂ - a₁₂a₂₁.

Его обозначают det A, или

.

Часто вместо слова «определитель» говорят «детерминант», откуда и взялось указанное обозначение.

Определитель третьего порядка определим через определители второго порядка:

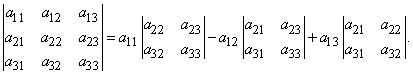
Здесь первые множители в знакочередующейся сумме - числа первой строки, а вторые множители - определители матриц, полученных вычеркиванием строки и столбца, которым принадлежит первый множитель.

Порядок определителя можно увеличивать и дальше. Пусть определены определители матриц вплоть до (n-1)-го порядка. Определителем матрицы n-го порядка

назовем число

где вновь имеем знакочередующуюся сумму произведений, в которых один из множителей - элемент первой строки, а другой - определитель матрицы (n-1)-го порядка, полученной вычеркиванием той строки и того столбца, которым принадлежит первый множитель.

Вычислим, например, определитель третьего порядка:

Определители играют важную роль в решении систем линейных уравнений.

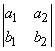
Любопытно, что если составить из координат двух векторов d = (a₁,a₂) и b = (b₁,b₂) определитель

,

то его величина, с точностью до знака, равна площади параллелограмма, построенного на этих векторах (рис. 1), а для трех векторов в пространстве 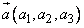, , 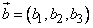 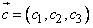определитель

равен, опять с точностью до знака, объему параллелепипеда, построенного на этих векторах (рис. 2).

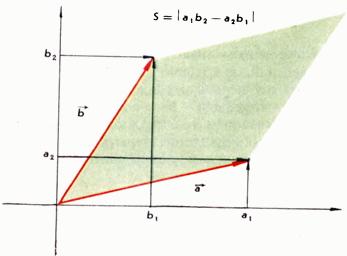
Рис. 1

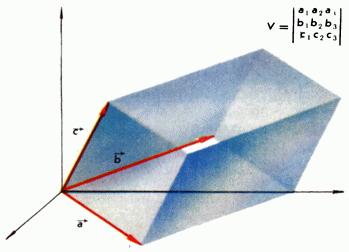
Рис. 2